Bienvenidos a nuestra sección dedicada a los Polinomios y su manipulación. Los polinomios son una herramienta esencial en las matemáticas, especialmente cuando se trata de expresar y resolver problemas algebraicos. En esta serie de ejercicios, te acompañaremos paso a paso en el mundo de los polinomios y su manejo.
La manipulación de un polinomio comienza asignando términos para cada componente de la expresión, junto con sus respectivos coeficientes. Cada término se representa mediante variables y exponentes, y podemos combinar, simplificar o resolver polinomios para abordar una variedad de situaciones matemáticas. Recuerda que un principio fundamental en el trabajo con polinomios es que podemos operar y combinar términos de manera sistemática para llegar a respuestas matemáticas precisas.
¿Has probado ya nuestras clases de matematicas a domicilio?
Indica cuáles de las siguientes expresiones son monomios. En caso de que la expresión sea un monomio, indica su grado y coeficiente.
a 
b 
c 
d 
e 
f 
g 
Recordemos que las únicas operaciones permitidas en un monomio son el producto y la potencia a un exponente natural. En los coeficientes puede aparecer cualquier operación.
a 
Sí es un monomio. Su coeficiente es 3 y su grado es 3.
b 
No es un monomio, ya que  se encuentra elevado a una potencia negativa (no es un número natural).
se encuentra elevado a una potencia negativa (no es un número natural).
c 
No es un monomio, ya que aparece una suma en la expresión.
d 
Sí es un monomio: la raíz puede aparecer en los coeficientes. El coeficiente es  y el grado es 1.
y el grado es 1.
e 
Sí es un monomio: aunque hay una división, se encuentra en el coeficiente. Así, el coeficiente es  y el grado es 4.
y el grado es 4.
f 
No es un monomio, pues hay una división que afecta a alguna variable.
g 
No es un monomio, puesto que una variable se encuentra afectada por una raíz. O lo que es lo mismo, la variable se encuentra elevada a una potencia fraccionar (1/2).
Di si las siguientes expresiones algebraicas son polinomios o no. En caso afirmativo, señala cuál es su grado y término independiente.
a 
b 
c 
d 
e 
f 
g 
Recordemos que un polinomio es una suma de monomios. El grado del polinomio será el grado de aquél monomio de mayor grado.
a 
Sí es un polinomio. Su grado es 5 y el término independiente también es 5.
b 
No es un polinomio ya que hay una raíz cuadrada presente.
c 
Sí es un polinomio. El grado es 4 y el término independiente es 1.
d 
No es un polinomio ya que el término  no es un monomio (se encuentra elevado a un número negativo).
no es un monomio (se encuentra elevado a un número negativo).
e 
Sí es un polinomio. El grado es 5 y el término independiente es 0.
f 
No es un polinomio pues el término  tiene una potencia a un número negativo.
tiene una potencia a un número negativo.
g 
Sí es un polinomio. El grado es 3 y el término independiente es 
Escribe:
a Un polinomio ordenado sin término independiente.
b Un polinomio no ordenado y completo.
c Un polinomio completo sin término independiente.
d Un polinomio de grado 4, que sea completo y cuyos coeficientes sean impares.
Esta pregunta es abierta y tiene muchas respuestas correctas. Por tanto, sólo mostramos algunas de las posibles respuestas.
a Un polinomio ordenado sin término independiente.
Cualquiera de los siguientes polinomios es correcto:


b Un polinomio no ordenado y completo.
Cualquiera de los siguientes polinomios es correcto:


c Un polinomio completo sin término independiente.
Este polinomio es imposible de construir. Para que un polinomio sea completo se debe tener un término independiente.
d Un polinomio de grado 4, que sea completo y cuyos coeficientes sean impares.
Cualquiera de los siguientes polinomios es correcto:


Evaluación de polinomios
Encuentra el valor numérico del polinomio  al evaluarlo en
al evaluarlo en
a 
b 
c 
Para evaluar el polinomio, simplemente sustituimos  por su valor en
por su valor en  :
:
a 
El valor es:

b 
Evaluamos:

c 
Por último, al evaluar en 2, tenemos

Operaciones con polinomios
Efectúa las siguientes operaciones con monomios:
a 
b 
c 
d 
e 
f 
g 
h 
i 
j 
k 
a 
Recordemos que en la suma de monomios, los coeficientes se suman (siempre que las variables tengan todas la misma potencia):

b 
Este caso es similar al anterior:

c 
En la multiplicación de monomios, los coeficientes se multiplican y las potencias se suman:

d 
Tenemos de nuevo una multiplicación de monomios. Sin embargo, recordemos que sólo se suman las potencias de las variables que coinciden:

e 
A diferencia de la multiplicación, en la división los coeficientes se dividen y las potencias se restan:

f 
Tenemos una división con más variables:

g 
En las potencias, los coeficientes se elevan a la potencia, y las potencias de las variables se multiplican por la potencia "exterior":

h 
Tenemos otra potencia:

i 
Tenemos otra suma de monomios:

j 
Ahora tenemos otra división:

k 
Esta última expresión combina distintas operaciones. Observemos que los monomios del denominador no se pueden sumar ya que no tienen el mismo grado. Sin embargo, podemos dividir cada uno de ellos por el denominado común:

Dados los polinomios

determina
a 
b 
c 
d 
e 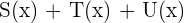
f 
En este ejercicio debemos realizar suma de polinomios. Recordemos que la suma se hace sumando los coeficientes de aquellos monomios con mismo grado.
a 
Tenemos

b 
Ahora el procedimiento es

c 
En este caso, tenemos

d 
En este caso, primero debemos multiplicar los coeficientes de  por 2:
por 2:

e 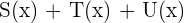
Este se resuelve igual que el caso anterior. La única diferencia es que

f 

Realiza las siguientes multiplicaciones de polinomios:
a 
b 
c 
Recordemos que para realizar la multiplicación, debemos utilizar la ley distributiva de los números.
a 
El procedimiento es como sigue:
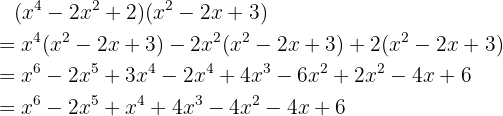
b 
Aquí la multiplicación es:
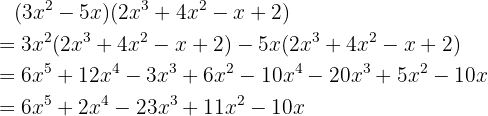
c 
El procedimiento es
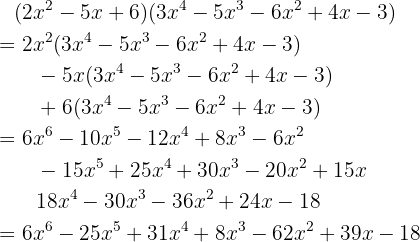
Productos notables
Evalúa los siguientes productos notables:
a 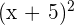
b 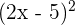
c 
d 
Se trata de binomios al cuadrado y binomios conjugados. Por tanto, simplemente utilizamos la fórmula.
a 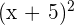
Recordemos que el binomio al cuadrado tiene la fórmula

Por tanto, la operación se resuelve utilizando

b 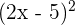
Al igual que el caso anterior, se trata de un binomio conjugado

c 
En este caso se trata de unos binomios conjugados. Recordemos que tiene la fórmula

De este modo, la operación se resuelve

d 
Estos también son binomios conjugados, de modo que resolvemos mediante

Desarrolla los siguientes productos notables
a 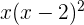
b 
c 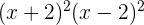
a 
Recordemos que
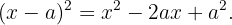
Entonces, para 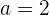 , obtenemos
, obtenemos
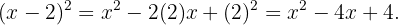
Por lo tanto, podemos concluir
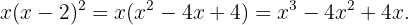
b 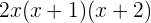
Recordemos que
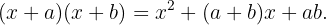
Entonces, para  , obtenemos
, obtenemos
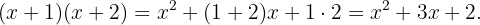
Por lo tanto, podemos concluir que
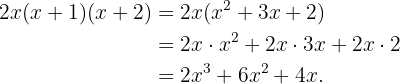
c 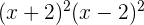
Expandiremos primero el término 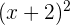 :
:
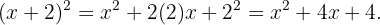
Ahora, el término 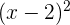 :
:
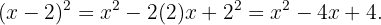
Por último, haremos el producto de ambas expresiones para obtener el resultado.
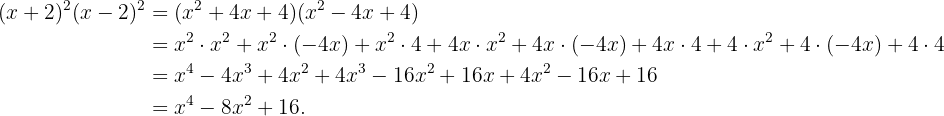
Evalua los polinomios del ejercicio 9 en los siguientes puntos:
a 
b 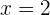
c 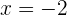
a 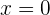
Sustituyendo 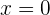 en el primero polinomio, obtenemos
en el primero polinomio, obtenemos
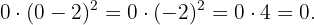
Para el segundo polinomio, tenemos
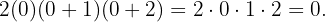
Para el tercero, tenemos
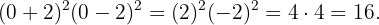
b 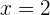
En el primer polinomio, obtenemos
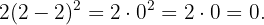
Para el segundo polinomio,
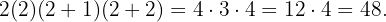
En el tercer polinomio, obtenemos
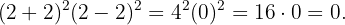
c 
En el primer polinomio, sustituir este valor resulta en
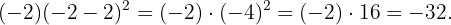
Para el segundo, obtenemos
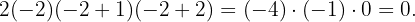
Por último, el tercero nos da
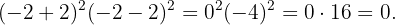
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Quiero mas ejemplos de monomios pero feciles
En el cálculo con polinomios creo que la 4 estaba mal
Hola revise el ejercicio y no encontré el error, pero al principio me confundí pues la solución esta arriba del número, no se si te paso a ti, si no fue así, podrías señalármelo por favor.
HAY MUCHOS ERRORES
Miren sus soluciones a los problemas, los errores en la resolucion de sus propios problemas son DEMACIADOS.
Un ejemplo en calculos con polinomios
(x²+2)² (a+b)²=a²+2ab+b²
(x²)²+2(x²)(2)+2²
resultado real= x⁴+4x²+4
el suyo es= x⁴+2x²+4
Los invito a realizar su chequeo ya que confunde y desmotiva el uso de la pagina a la gran mayoria que estamos aprendiendo.
Hola te agradecemos tus comentarios, el error que mencionas ya se corrigió, si encuentras algún otro con gusto te atenderemos.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado