Capítulos
En este artículo exploraremos la factorización de polinomios. Primero expondremos algunos teoremas y propiedades sobre los polinomios que nos ayudarán a factorizarlos con mayor facilidad. Luego revisaremos con detalle métodos para factorizarlos y al final mostraremos algunos ejemplos de factorización de polinomios.

Teoremas sobre los factores de un polinomio
Para los siguientes teoremas recordemos que  es una raíz del polinomio
es una raíz del polinomio  si se cumple que
si se cumple que 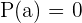 .
.
Teorema del Resto
Teorema: El resto o residuo de la división de un polinomio  por un polinomio de la forma
por un polinomio de la forma  es igual que el resultado de evaluar el polinomio
es igual que el resultado de evaluar el polinomio  en
en  .
.
Por ejemplo, dividamos 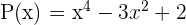 entre
entre  utilizando la regla de Ruffini:
utilizando la regla de Ruffini:
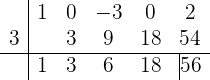
Así, el cociente de la división es 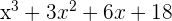 , mientras que el residuo es 56. Por otro lado, si evaluamos
, mientras que el residuo es 56. Por otro lado, si evaluamos  en 3, obtenemos:
en 3, obtenemos:

Nota: Observemos que si 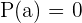 , entonces significa que el residuo es 0. En otras palabras:
, entonces significa que el residuo es 0. En otras palabras:
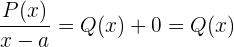
Si multiplicamos ambos lados por  tenemos que
tenemos que

Por lo tanto,  es un factor de
es un factor de  . Este resultado se conoce como el teorema del factor.
. Este resultado se conoce como el teorema del factor.
Teorema del factor
Teorema: El polinomio  es divisible por un polinomio de la forma
es divisible por un polinomio de la forma  si y sólo si
si y sólo si 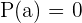 .
.
Como ejemplo, consideremos el polinomio 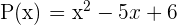 . Notemos que
. Notemos que

por lo tanto,  . Además,
. Además,  y
y  son raíces de
son raíces de  .
.
Nota: Si  es un polinomio de grado
es un polinomio de grado  y se divide por
y se divide por  , entonces el resultado tiene la forma:
, entonces el resultado tiene la forma:

donde  es constante y se conoce como residuo, mientras que
es constante y se conoce como residuo, mientras que  es un polinomio de grado
es un polinomio de grado  .
.
Teorema Fundamental del Álgebra
Teorema: Un polinomio 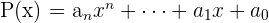 de grado
de grado  y con coeficientes reales
y con coeficientes reales  tiene exactamente
tiene exactamente  raíces, las cuales pueden ser reales o complejas.
raíces, las cuales pueden ser reales o complejas.
Nota: Los polinomios reales tienen  raíces, sin embargo, es posible que ninguna sea real. Cuando ninguna raíz es real entonces el polinomio
raíces, sin embargo, es posible que ninguna sea real. Cuando ninguna raíz es real entonces el polinomio  no se puede factorizar en factores lineales.
no se puede factorizar en factores lineales.
Nota: Recordemos que factorizar un polinomio  en factores lineales significa escribir
en factores lineales significa escribir  de la forma
de la forma

en donde  son las raíces de
son las raíces de  .
.
Teorema de la Raíz Racional
Teorema: Sea  un polinomio con coeficientes
un polinomio con coeficientes  que son enteros. Si
que son enteros. Si 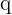 es una raíz racional de
es una raíz racional de  , entonces
, entonces 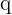 tendrá la forma
tendrá la forma
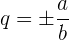
donde  es un factor de
es un factor de 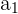 y
y  es un factor de
es un factor de  .
.
Nota: Este teorema, junto con el teorema del factor, nos ayudan a encontrar raíces rápido. Primero enlistamos todas las posibles raíces racionales 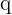 de
de  , luego evaluamos
, luego evaluamos  . Si
. Si 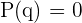 , entonces sabremos que
, entonces sabremos que 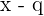 es un factor de
es un factor de  . Describiremos algunos ejemplos en la sección de ejemplos.
. Describiremos algunos ejemplos en la sección de ejemplos.
Nota: Este teorema sólo nos dice la forma que tendrán las raíces racionales. Es posible que un polinomio no tenga ninguna raíz racional como en el caso de  , cuyas raíces son
, cuyas raíces son  y
y 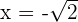 .
.
Nota: Si 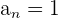 , entonces el polinomio se conoce como mónico. En este caso, el único factor de
, entonces el polinomio se conoce como mónico. En este caso, el único factor de  es 1, por lo tanto, las raíces tienen la forma
es 1, por lo tanto, las raíces tienen la forma

donde  es un factor de
es un factor de 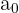 .
.
Algunas propiedades de las raíces y los factores de un polinomio
1 A cada raíz  le corresponde un binomio del tipo
le corresponde un binomio del tipo  como factor.
como factor.
2 Supongamos que  es una raíz de
es una raíz de  . Entonces, podemos escribir
. Entonces, podemos escribir  como
como
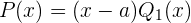
donde  es un polinomio de grado
es un polinomio de grado  . Después, si descubrimos que
. Después, si descubrimos que  también es raíz de
también es raíz de  , por lo tanto,
, por lo tanto,  se podría escribir como
se podría escribir como
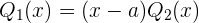
De aquí se sigue que  se puede escribir como
se puede escribir como
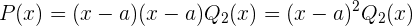
Si 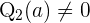 , entonces diríamos que
, entonces diríamos que  es una raíz de multiplicidad 2 de
es una raíz de multiplicidad 2 de  . Esto implica que las
. Esto implica que las  raíces del polinomio
raíces del polinomio  no son necesariamente todas distintas.
no son necesariamente todas distintas.
3 Podemos expresar un polinomio en factores al escribirlo como producto de todos los binomios del tipo  que correspondan a las raíces
que correspondan a las raíces  del polinomio. Así,
del polinomio. Así,  se factoriza como
se factoriza como

Por ejemplo, ya que  y
y  son raíces del polinomio
son raíces del polinomio 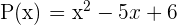 , entonces podemos escribir
, entonces podemos escribir
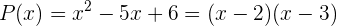
4 Todo polinomio que no tenga un término independiente tendrá a  como raíz. Por lo tanto, también tendrá a
como raíz. Por lo tanto, también tendrá a  como factor (es decir,
como factor (es decir, 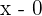 ).
).
Por ejemplo, el polinomio 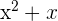 se puede factorizar como
se puede factorizar como 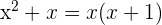 . De aquí, concluímos que las raíces son
. De aquí, concluímos que las raíces son  y
y  .
.
5 Un polinomio es irreducible o primo si no puede descomponerse en factores.
Por ejemplo, el polinomio  no se puede factorizar ya que las raíces son complejas.
no se puede factorizar ya que las raíces son complejas.
Métodos para factorizar un polinomio
Factor común
Sacar el factor común consiste en aplicar la propiedad distributiva de los números reales:

Por ejemplo, consideremos el polinomio 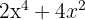 . Notemos que cada término se puede dividir por
. Notemos que cada término se puede dividir por 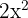 (es decir, es el factor común). Por lo tanto, el polinomio lo podemos factorizar como
(es decir, es el factor común). Por lo tanto, el polinomio lo podemos factorizar como
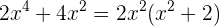
Observemos que el polinomio  no se puede factorizar, por lo tanto, esto es lo más que podemos factorizar el polinomio. La única raíz del polinomio es
no se puede factorizar, por lo tanto, esto es lo más que podemos factorizar el polinomio. La única raíz del polinomio es  con multiplicidad 2.
con multiplicidad 2.
Productos notables
Existen algunos polinomios de segundo grado que son muy sencillos de factorizar ya que tienen una estructura fácilmente reconocible. Los más comunes son:
1 Diferencia de cuadrados: si el polinomio se puede escribir de la forma 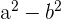 , entonces podemos factorizar como
, entonces podemos factorizar como 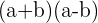 .
.
Por ejemplo, los polinomios 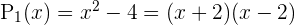 o
o 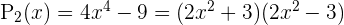 .
.
2 Trinomio cuadrado perfecto: si el polinomio tiene la forma 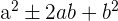 , entonces lo podemos factorizar como
, entonces lo podemos factorizar como  .
.
Por ejemplo, consideremos el polinomio 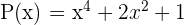 (donde
(donde 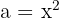 y
y  ), el cual se puede factorizar como
), el cual se puede factorizar como 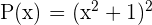 .
.
Nota: existen otros productos notables, como el cubo perfecto de binomios. Sin embargo, esos no son tan conmunes.
Con el teorema de la raíz racional
Si no tenemos un factor común o no se puede escribir el polinomio como un producto notable, entonces podemos intentar a utilizar el teorema de la raíz racional (siempre que todos los coeficientes del polinomio sean enteros). Aquí evaluamos el polinomio  entre todas las posibles raíces racionales
entre todas las posibles raíces racionales 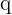 buscado alguna que satisfaga que
buscado alguna que satisfaga que 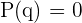 . En este caso, utilizamos la regla de Ruffini para realizar la factorización de la forma:
. En este caso, utilizamos la regla de Ruffini para realizar la factorización de la forma:

Luego repetimos el procedimiento con  (pero descargamos aquellos valores
(pero descargamos aquellos valores 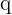 que ya sabemos que no son factores).
que ya sabemos que no son factores).
Utilizando la fórmula general
Si el polinomio es de segundo grado (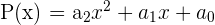 ) y todos los métodos anteriores fallaron, entonces podemos utilizar la fórmula general:
) y todos los métodos anteriores fallaron, entonces podemos utilizar la fórmula general:
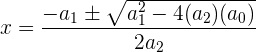
esto nos dará las dos raíces del polinomio  y
y  y el polinomio lo podremos factorizar como
y el polinomio lo podremos factorizar como 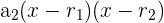 .
.
Nota: Si las raíces son complejas, podemos obtar por dejar el polinomio sin factorizar y decir que es irreducible. También es posible factorizarlo utilizando las raíces complejas, sin embargo, en este caso los factores serán polinomios en los números complejos.
Nota: Si el polinomio es de grado mayor a 2 todo lo anterior falla, entonces es posible que todas las raíces sean irracionales o complejas. En este caso lo más apropiado es utilizar algún método numérico o un programa de computadora para factorizar el polinomio.
Ejemplos
Encuentra las raíces del polinomio 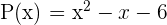 y factorízalo.
y factorízalo.
Por el teorema de la raíz racional sabemos que las raíces racionales serán de la forma  ; ya que el polinomio es mónico y el término constante es 6 cuyos factores son 1, 2, 3 y 6 (todos los factores, no sólo los primos).
; ya que el polinomio es mónico y el término constante es 6 cuyos factores son 1, 2, 3 y 6 (todos los factores, no sólo los primos).
Al evaluar el polinomio en estos 8 posibles valores tenemos  ,
, 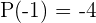 ,
, 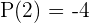 ,
, 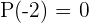 (de aquí ya sabemos que
(de aquí ya sabemos que  es una raíz),
es una raíz),  (de donde sabemos que
(de donde sabemos que  también es una raíz, por lo que nos detenemos de evaluar ya que ya encontramos las dos raíces).
también es una raíz, por lo que nos detenemos de evaluar ya que ya encontramos las dos raíces).
Por lo tanto, el polinomio  lo podemos factorizar como
lo podemos factorizar como
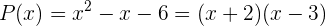
Encuentra las raíces del polinomio 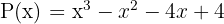 y factorízalo.
y factorízalo.
Por el teorema de la raíz racional sabemos que las raíces racionales serán de la forma 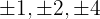 ; ya que el polinomio es mónico y el término constante es 4 cuyos factores son 1, 2 y 4 (todos los factores, no sólo los primos).
; ya que el polinomio es mónico y el término constante es 4 cuyos factores son 1, 2 y 4 (todos los factores, no sólo los primos).
Al evaluar el polinomio en estos 6 posibles valores tenemos 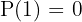 ,
, 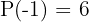 ,
, 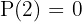 ,
, 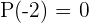 (de aquí ya sabemos que
(de aquí ya sabemos que 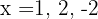 son raices), por lo que nos detenemos de evaluar ya que ya encontramos las tres raíces).
son raices), por lo que nos detenemos de evaluar ya que ya encontramos las tres raíces).
Por lo tanto, el polinomio  lo podemos factorizar como
lo podemos factorizar como
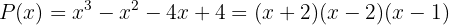
Factoriza los siguientes polinomios utilizando la fórmula general:
a 
b 
c 
Se nos pide utilizar la fórmula general, por lo que eso haremos para cada polinomio:
a Primero tenemos  ,
,

por lo tanto, una raíz es  y la otra raíz es
y la otra raíz es 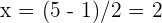 . De aquí, se sigue que el polinomio se factoriza como
. De aquí, se sigue que el polinomio se factoriza como

b Para  tenemos
tenemos
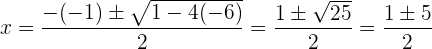
por lo tanto, una raíz es 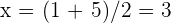 y la otra raíz es
y la otra raíz es 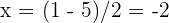 . De aquí, se sigue que el polinomio se factoriza como
. De aquí, se sigue que el polinomio se factoriza como
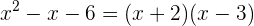
c Por último, para  notemos que no tenemos un polinomio de segundo grado. Sin embargo, solo tenemos las potencias 2 y 4, de manera que podemos hacer el cambio de variable
notemos que no tenemos un polinomio de segundo grado. Sin embargo, solo tenemos las potencias 2 y 4, de manera que podemos hacer el cambio de variable  ,
,

Este polinomio ya es de segundo grado, por lo que podemos utilizar la fórmula general,

De aquí, tenemos que las raíces son 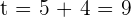 y
y 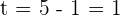 . No obstante,
. No obstante,  , por lo que tenemos
, por lo que tenemos
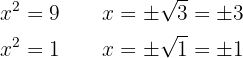
De esta forma, el polinomio queda factorizado como

Factoriza el siguiente polinomio de tercer grado:
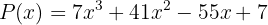
Como el polinomio es de tercer grado y tiene coeficientes enteros, entonces utilizaremos el teorema de la raíz racional para enlistar todas las posibles raíces racionales.
El coeficiente principal es 7, cuyos factores son 1 y 7. El coeficiente independiente es 7, que tiene factores 1 y 7. De esta forma, las posibles raíces son
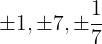
Nota que descartamos 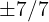 ya que es igual a
ya que es igual a  .
.
Ahora evaluamos el polinomio en estos valores para encontrar las raíces:
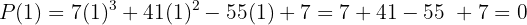
Notamos que el  es una raíz. Por lo tanto, utilizamos la regla de Ruffini:
es una raíz. Por lo tanto, utilizamos la regla de Ruffini:
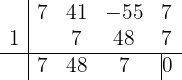
Es decir,  y
y 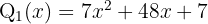 son factores.
son factores.
Notemos que el último factor es cuadrático, por lo que podemos utilizar la fórmula general:
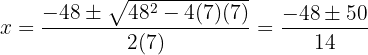
Por lo tanto, las raíces restantes son 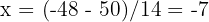 y
y 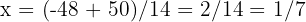 .
.
Es decir, las tres raíces son
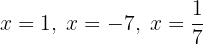
Por último, el polinomio se factoriza como (recordemos que el coeficiente principal siempre lo dejamos fuera de los factores lineales):
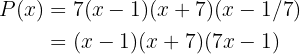
donde multiplicamos el último factor por el 7 para deshacernos de la fracción.
Factoriza el siguiente polinomio de cuarto grado:

Como el polinomio es de cuarto grado y tiene coeficientes enteros, entonces utilizaremos el teorema de la raíz racional para enlistar todas las posibles raíces racionales.
El coeficiente principal es 2, cuyos factores son 1 y 2. El coeficiente independiente es 6, que tiene factores 1, 2, 3 y 6. De esta forma, las posibles raíces son
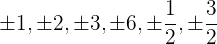
Nota que descartamos  ya que es igual a
ya que es igual a  ; al igual que descartamos
; al igual que descartamos 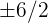 ya que es igual a
ya que es igual a 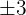 .
.
Ahora evaluamos el polinomio en estos valores para encontrar las raíces:
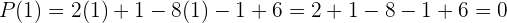
Notamos que el  es una raíz. Por lo tanto, utilizamos la regla de Ruffini:
es una raíz. Por lo tanto, utilizamos la regla de Ruffini:
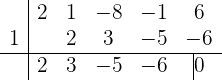
Es decir,  y
y  son factores.
son factores.
Seguimos realizando el procedimiento, ahora con evaluando  en las posibles raíces (volvemos a intentar con 1, por si es una raíz de multiplicidad mayor):
en las posibles raíces (volvemos a intentar con 1, por si es una raíz de multiplicidad mayor):
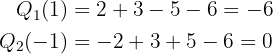
por lo que  también es raíz. Utilizamos la regla de Ruffini de nuevo:
también es raíz. Utilizamos la regla de Ruffini de nuevo:
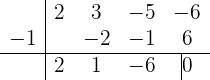
de forma que los factores son  y
y 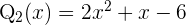 .
.
Notemos que el último factor es cuadrático, por lo que podemos utilizar la fórmula general:

Por lo tanto, las raíces restantes son 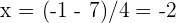 y
y 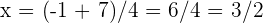 .
.
Es decir, las cuatro raíces son
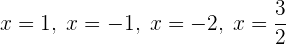
Por último, el polinomio se factoriza como (recordemos que el coeficiente principal siempre lo dejamos fuera de los factores lineales):
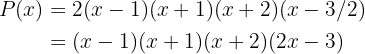
donde multiplicamos el último factor por el 2 para deshacernos de la fracción.
¿Conoces nuestras clases particulares matematicas Madrid?
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el cálculo con polinomios creo que la 4 estaba mal
Hola revise el ejercicio y no encontré el error, pero al principio me confundí pues la solución esta arriba del número, no se si te paso a ti, si no fue así, podrías señalármelo por favor.
HAY MUCHOS ERRORES
Miren sus soluciones a los problemas, los errores en la resolucion de sus propios problemas son DEMACIADOS.
Un ejemplo en calculos con polinomios
(x²+2)² (a+b)²=a²+2ab+b²
(x²)²+2(x²)(2)+2²
resultado real= x⁴+4x²+4
el suyo es= x⁴+2x²+4
Los invito a realizar su chequeo ya que confunde y desmotiva el uso de la pagina a la gran mayoria que estamos aprendiendo.
Hola te agradecemos tus comentarios, el error que mencionas ya se corrigió, si encuentras algún otro con gusto te atenderemos.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado