Capítulos
En este artículo explicamos los productos notables más comúnes acompañados de ejemplos puntuales para profundizar en la teoría.
¿Qué son los productos notables? Los productos notables son simplemente multiplicaciones especiales entre expresiones algebraicas las cuales sobresalen de las demás multiplicaciones por su frecuente aparición en matemáticas. De ahí el nombre producto, que hace referencia a "multiplicación" y notable, que hace referencia a su "destacada" aparición.
Así bien, una vez aprendido dichos productos notables, no habrá necesidad de comprobar dicha multiplicación mecánicamente, es decir, solo debemos seguir las reglas aprendidas con anterioridad que caracterizan a cada producto notable.

Binomio al cuadrado
Un binomio al cuadrado es igual al cuadrado del primero, más el doble del primero por el segundo, más el cuadrado del segundo.
Si los dos signos del binomio son iguales, el doble del primero por el segundo es positivo.
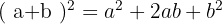
Si los signos del binomio son distintos, el doble del primero por el segundo es negativo.
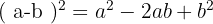
Ejemplos de ejercicios con binomios al cuadrado
1 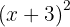
Para resolver este caso usamos la primer fórmula tomando 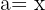 y
y  , sustituimos y nos queda
, sustituimos y nos queda
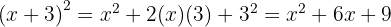
2 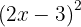
Para resolver este caso usamos la segunda fórmula tomando 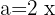 y
y  , sustituimos y nos queda
, sustituimos y nos queda

3 
Para resolver este caso usamos la primer fórmula tomando 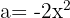 y
y  , sustituimos y nos queda
, sustituimos y nos queda
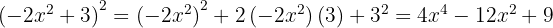
4 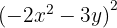
Para resolver este caso usamos la primer fórmula tomando 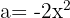 y
y  , sustituimos y nos queda
, sustituimos y nos queda
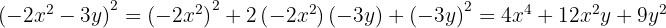
Repasa las identidades notables con un profesor de matematicas.
Suma por diferencia
Una suma por diferencia es igual a diferencia de cuadrados.

Ejemplos de ejercicios con suma por diferencia
1 
Usando la fórmula llamamos a  y
y  , entonces sustituimos y nos queda
, entonces sustituimos y nos queda

2 
Usando la fórmula llamamos a  y
y  , entonces sustituimos y nos queda
, entonces sustituimos y nos queda

Binomio al cubo
Un binomio al cubo es igual al cubo del primero más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
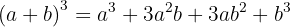
Recomendamos aprenderte esta fórmula.
Ejemplos de ejercicios con binomios al cubo
1 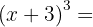
Usando la fórmula llamamos a 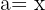 y
y  , entonces sustituimos y nos queda
, entonces sustituimos y nos queda
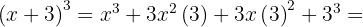
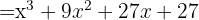
2 
Usando la fórmula llamamos a 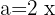 y
y 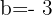 , entonces sustituimos y nos queda
, entonces sustituimos y nos queda

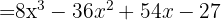
Si nos fijamos en los signos obtenidos: +, −, +, −. Podemos dar una variante a la fórmula anterior:
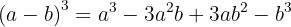
3 
Usando la fórmula de 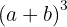 llamamos a
llamamos a  y
y 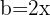 , entonces sustituimos y nos queda
, entonces sustituimos y nos queda
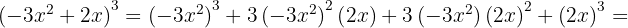
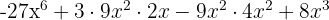
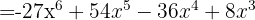
Los signos obtenidos son: −, +, −, +. Podemos dar otra variante:
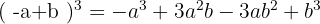
4 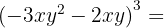
Usando la fórmula de 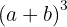 llamamos a
llamamos a  y
y 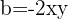 , entonces sustituimos y nos queda
, entonces sustituimos y nos queda


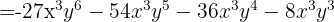
Los signos obtenidos son: −, −, −, −. Podemos dar otra variante:
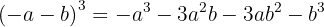
Trinomio al cuadrado
Un trinomio al cuadrado es igual al cuadrado del primero, más el cuadrado del segundo, más el cuadrado del tercero, más el doble producto del primero por el segundo, más el doble producto del primero por el tercero, más el doble producto del segundo por el tercero.

Ejemplos de ejercicios con trinomios al cuadrado
1 
Para resolver este ejercicio tomamos 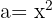 ,
, 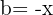 y
y  , sustituimos en la fórmula y nos queda
, sustituimos en la fórmula y nos queda
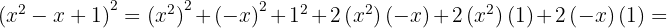
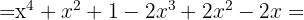

2 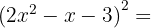
Para resolver este ejercicio tomamos  ,
, 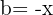 y
y 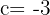 , sustituimos en la fórmula y nos queda
, sustituimos en la fórmula y nos queda

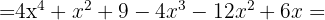
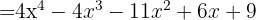
¿Estás buscando un profesor mates? ¡Encuéntralo en Superprof!
Suma de cubos
Ahora en vez de desarrollar a las expresiones, lo que haremos será factorizarlas, es decir, las escribiremos como el producto de otras dos expresiones.
La forma en que se factoriza la suma de cubos es la siguiente:
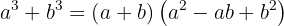
Ejemplo de ejercicio con suma de cubos
Factorizar la expresión siguiente:
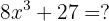
Primero, miramos como podemos reescribir los términos para usar la fórmula de factorización de cubos. En este caso, podemos reescribir la expresión de la manera siguiente:
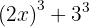
Utilizando la fórmula de cubos y considerando que 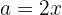 y
y  , tenemos:
, tenemos:
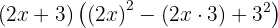
Desarollando, tenemos:
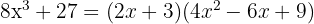
Diferencia de cubos
La fórmula para diferencia de cubos tiene la siguiente estructura:
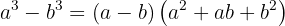
Ejemplo de ejercicio con diferencia de cubos
Factorizar la expresión siguiente:

Igual que anteriormente, es importante mirar, en primer lugar, como podemos reescribir los términos para usar la fórmula de factorización de cubos. En este caso, podemos reescribir la expresión de la manera siguiente:
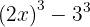
Utilizando la fórmula de cubos y considerando que 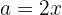 y
y  , tenemos:
, tenemos:
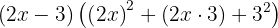
Desarollando, tenemos:
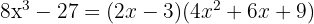
Producto de dos binomios que tienen un término común
Cuando se presenta le producto de dos binomios con término común, es más simple el desarrollo y queda de la siguiente manera:
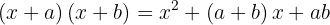
Ejemplo de ejercicio con producto de dos binomios con término común
Desarollar la expresión siguiente:
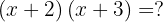
No es necesario recordar la fórmula, si, siguiendo los pasos de desarrollo y con atención a los signos, simplemente operamos paso a paso.
Primero, tomamos los términos dentro del primer paréntesis y los multiplicamos con la segunda de esta manera:
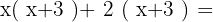
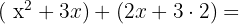
Recomendamos guardar los paréntesis y deshacerlos posteriormente. Así, nos aseguramos de no haber olvidado cambiar un + por un - o al revés. En este caso, no hay ningún cambio de signo.
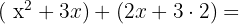
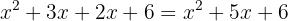
Ejemplos de ejercicios resueltos de productos notables
Desarrolla los binomios al cuadrado.
1 
Usamos la fórmula  , donde
, donde  y
y  , sustituimos y nos queda
, sustituimos y nos queda

2 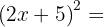
Usamos la fórmula  , donde
, donde  y
y  , sustituimos y nos queda
, sustituimos y nos queda
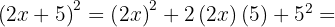
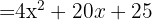
3 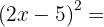
Usamos la fórmula 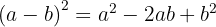 , donde
, donde  y
y  , sustituimos y nos queda
, sustituimos y nos queda
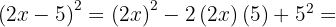
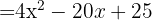
4 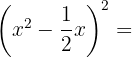
Usamos la fórmula 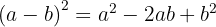 , donde
, donde  y
y 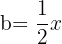 , sustituimos y nos queda
, sustituimos y nos queda
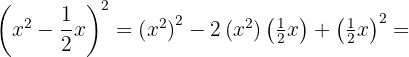
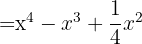
Desarrolla los binomios al cubo.
1 
Usamos la fórmula 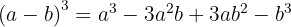 , donde
, donde  y
y  , sustituyendo nos queda
, sustituyendo nos queda
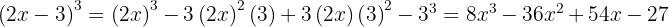
2 
Usamos la fórmula 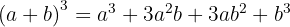 , donde
, donde  y
y 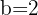 , sustituyendo nos queda
, sustituyendo nos queda
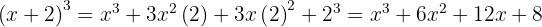
3 
Usamos la fórmula 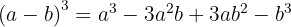 , donde
, donde 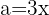 y
y 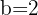 , sustituyendo nos queda
, sustituyendo nos queda
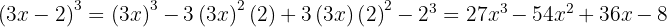
4 
Usamos la fórmula 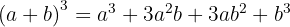 , donde
, donde  y
y  , sustituyendo nos queda
, sustituyendo nos queda
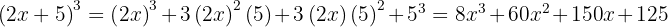
Desarrolla las sumas por diferencias
1 
Usamos la fórmula 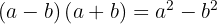 , donde
, donde 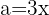 y
y 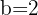 , sustituyendo nos queda
, sustituyendo nos queda
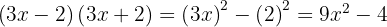
2 
Usamos la fórmula 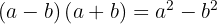 , donde
, donde  y
y  , sustituyendo nos queda
, sustituyendo nos queda

3 
Usamos la fórmula 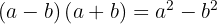 , donde
, donde 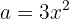 y
y  , sustituyendo nos queda
, sustituyendo nos queda

4 
Usamos la fórmula 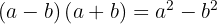 , donde
, donde 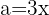 y
y  , sustituyendo nos queda
, sustituyendo nos queda
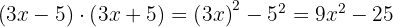
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el cálculo con polinomios creo que la 4 estaba mal
Hola revise el ejercicio y no encontré el error, pero al principio me confundí pues la solución esta arriba del número, no se si te paso a ti, si no fue así, podrías señalármelo por favor.
HAY MUCHOS ERRORES
Miren sus soluciones a los problemas, los errores en la resolucion de sus propios problemas son DEMACIADOS.
Un ejemplo en calculos con polinomios
(x²+2)² (a+b)²=a²+2ab+b²
(x²)²+2(x²)(2)+2²
resultado real= x⁴+4x²+4
el suyo es= x⁴+2x²+4
Los invito a realizar su chequeo ya que confunde y desmotiva el uso de la pagina a la gran mayoria que estamos aprendiendo.
Hola te agradecemos tus comentarios, el error que mencionas ya se corrigió, si encuentras algún otro con gusto te atenderemos.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado