Capítulos

Enunciado del teorema
Recordemos que al dividir un polinomio  por otro
por otro  obtenemos un cociente
obtenemos un cociente  y un residuo
y un residuo 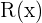 tales que
tales que
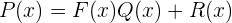
en donde el grado de 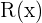 es estrictamente menor al grado de
es estrictamente menor al grado de  . Otra forma de escribir la división es:
. Otra forma de escribir la división es:

El teorema del resto nos ayuda a determinar el residuo o resto 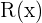 al dividir
al dividir  por un polinomio de la forma
por un polinomio de la forma 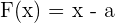 . El teorema enuncia lo siguiente:
. El teorema enuncia lo siguiente:
Teorema: Sea  un polinomio. Entonces el residuo resultante al dividir
un polinomio. Entonces el residuo resultante al dividir  entre
entre 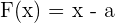 es igual que el resultado de evaluar el polinomio
es igual que el resultado de evaluar el polinomio  en
en  . Es decir,
. Es decir,

Ejemplo: Consideremos los polinomios 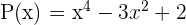 y
y 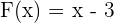 . Tenemos que
. Tenemos que
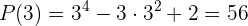
Por lo tanto, el residuo que resulta al dividir  entre
entre  debería ser 56. Para verificarlo, utilizaremos la regla de Ruffini; primero colocamos los coeficientes del polinomio
debería ser 56. Para verificarlo, utilizaremos la regla de Ruffini; primero colocamos los coeficientes del polinomio  en la primera fila de nuestro arreglo y colocamos el 3 ligeramente a la izquierda:
en la primera fila de nuestro arreglo y colocamos el 3 ligeramente a la izquierda:
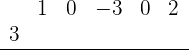
Luego, bajamos el 1 (el primer coeficiente de  ) debajo de la línea horizontal:
) debajo de la línea horizontal:
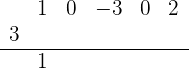
Después multiplicamos el 1 que tenemos debajo de la línea horizontal por el 3 (cuyo resultado es 3) y lo colocamos debajo del siguiente coeficiente de  :
:

Después realizamos la resta de los números que están en la columna del segundo coeficiente (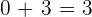 ) y colocamos el resultado debajo de la línea horizontal:
) y colocamos el resultado debajo de la línea horizontal:
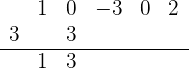
Repetimos el procedimiento anterior. Multiplicamos el número que obtuvimos debajo de la línea horizontal por el 3 (cuyo resultado será 9); lo colocamos debajo del siguiente coeficiente de  y luego sumamos los números:
y luego sumamos los números:
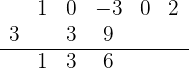
Repetimos el procedimiento, ahora con el 6:
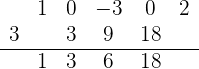
Finalmente, repetimos el procedimiento una vez más, pero ahora con el 18:
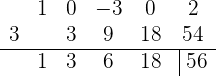
De este último arreglo podemos ver que 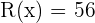 , que era lo que esperábamos.
, que era lo que esperábamos.
Nota: como podemos ver en el ejemplo anterior, el teorema del resto sólo nos dice el residuo que resulta al dividir por un polinomio. Si queremos encontrar el cociente  debemos realizar la división completa.
debemos realizar la división completa.
Nota: el teorema asume que estamos dividiendo por un polinomio de la forma 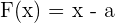 . Si tenemos algún polinomio de la forma
. Si tenemos algún polinomio de la forma  , entonces notemos que
, entonces notemos que
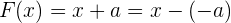
Por tanto, para encontrar el residuo, simplemente evaluamos 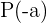 . En otras palabras, debemos evaluar en el término independiente de
. En otras palabras, debemos evaluar en el término independiente de  pero con signo cambiado.
pero con signo cambiado.
Nota: Este teorema es muy importante, pues no permite saber si un polinomio es factor de  . Sabremos que
. Sabremos que  es factor de
es factor de  si
si 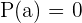 . Esto se conoce como teorema del factor.
. Esto se conoce como teorema del factor.
Ejercicios
Calcula, utilizando el teorema del resto, el residuo de la división de 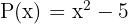 entre
entre  . Luego, comprueba con la regla de Ruffini.
. Luego, comprueba con la regla de Ruffini.
1 Primero utilizaremos el teorema del resto. Para esto, debemos evaluar el polinomio en  :
:
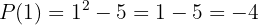
Por lo que el residuo es -4, lo cual nos indica que  no es factor de
no es factor de  .
.
2 Ahora verificaremos utilizando la regla de Ruffini. Empezamos colocando los coeficientes del polinomio en la primera fila (recordemos que debemos colocar todos los coeficientes, incluso los de los términos  ); luego colocamos el 1 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
); luego colocamos el 1 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
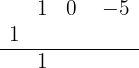
Multiplicamos el número que está debajo de la línea horizonal por el 1, y lo colocamos debajo del coeficiente del segundo término. Después, sumamos los términos de esa columna:
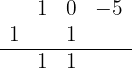
Repetimos el procedimiento para el siguiente número que está debajo de la línea horizontal:
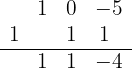
Donde podemos comprobar que, efectivamente, el residuo de la división es -4.
Calcula, utilizando el teorema del resto, el residuo de la división de 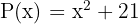 entre
entre  . Luego, comprueba con la regla de Ruffini.
. Luego, comprueba con la regla de Ruffini.
1 Primero utilizaremos el teorema del resto. Para esto, debemos evaluar el polinomio en  :
:
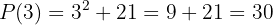
Por lo que el residuo es 30, lo cual nos indica que  no es factor de
no es factor de  .
.
2 Ahora verificaremos utilizando la regla de Ruffini. Empezamos colocando los coeficientes del polinomio en la primera fila (recordemos que debemos colocar todos los coeficientes, incluso los de los términos  ); luego colocamos el 3 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
); luego colocamos el 3 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
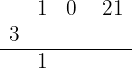
Multiplicamos el número que está debajo de la línea horizonal por el 3, y lo colocamos debajo del coeficiente del segundo término. Después, sumamos los términos de esa columna:
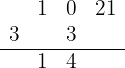
Repetimos el procedimiento para el siguiente número que está debajo de la línea horizontal:
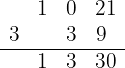
Donde podemos comprobar que, efectivamente, el residuo de la división es 30.
Calcula, utilizando el teorema del resto, el residuo de la división de 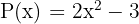 entre
entre  . Luego, comprueba con la regla de Ruffini.
. Luego, comprueba con la regla de Ruffini.
1 Primero utilizaremos el teorema del resto. Para esto, debemos evaluar el polinomio en  :
:
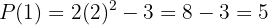
Por lo que el residuo es 5, lo cual nos indica que  no es factor de
no es factor de  .
.
2 Ahora verificaremos utilizando la regla de Ruffini. Empezamos colocando los coeficientes del polinomio en la primera fila (recordemos que debemos colocar todos los coeficientes, incluso los de los términos  ); luego colocamos el 2 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
); luego colocamos el 2 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
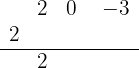
Multiplicamos el número que está debajo de la línea horizonal por el 2, y lo colocamos debajo del coeficiente del segundo término. Después, sumamos los términos de esa columna:
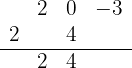
Repetimos el procedimiento para el siguiente número que está debajo de la línea horizontal:
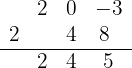
Donde podemos comprobar que, efectivamente, el residuo de la división es 5.
Calcula, utilizando el teorema del resto, el residuo de la división de 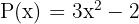 entre
entre  . Luego, comprueba con la regla de Ruffini.
. Luego, comprueba con la regla de Ruffini.
1 Primero utilizaremos el teorema del resto. Para esto, debemos evaluar el polinomio en 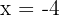 :
:
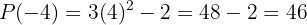
Por lo que el residuo es 46, lo cual nos indica que 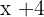 no es factor de
no es factor de  .
.
2 Ahora verificaremos utilizando la regla de Ruffini. Empezamos colocando los coeficientes del polinomio en la primera fila (recordemos que debemos colocar todos los coeficientes, incluso los de los términos  ); luego colocamos el -4 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
); luego colocamos el -4 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
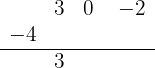
Multiplicamos el número que está debajo de la línea horizonal por el -4, y lo colocamos debajo del coeficiente del segundo término. Después, sumamos los términos de esa columna:
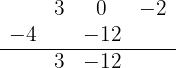
Repetimos el procedimiento para el siguiente número que está debajo de la línea horizontal:
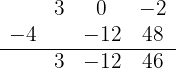
Donde podemos comprobar que, efectivamente, el residuo de la división es 46.
Calcula, utilizando el teorema del resto, el residuo de la división de 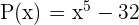 entre
entre  . Luego, comprueba con la regla de Ruffini.
. Luego, comprueba con la regla de Ruffini.
1 Primero utilizaremos el teorema del resto. Para esto, debemos evaluar el polinomio en  :
:
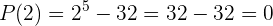
Por lo que el residuo es 0, lo cual nos indica que  es factor de
es factor de  .
.
2 Ahora verificaremos utilizando la regla de Ruffini. Empezamos colocando los coeficientes del polinomio en la primera fila (recordemos que debemos colocar todos los coeficientes, incluso los de los términos  ,
,  , etcétera); luego colocamos el 2 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
, etcétera); luego colocamos el 2 ligeramente a la izquierda y bajamos el primer coeficiente del polinomio:
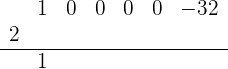
Multiplicamos el número que está debajo de la línea horizonal por el 2, y lo colocamos debajo del coeficiente del segundo término. Después, sumamos los términos de esa columna:
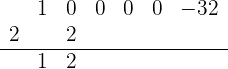
Repetimos el procedimiento para el siguiente número que está debajo de la línea horizontal:

Repetimos de nuevo:

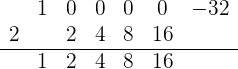
y por último, obtenemos:
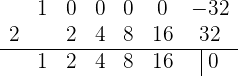
Donde podemos comprobar que, efectivamente, el residuo de la división es 0.
Considera el polinomio 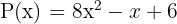 . Encuentra el residuo que resulta al dividir por
. Encuentra el residuo que resulta al dividir por 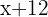
Utilizaremos el teorema del residuo
Basta con evaluar 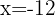 en
en  , es decir,
, es decir,
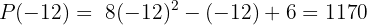
Considera el polinomio 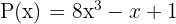 . Encuentra el residuo que resulta al dividir por
. Encuentra el residuo que resulta al dividir por 
Utilizaremos el teorema del residuo
Basta con evaluar  en
en  , es decir,
, es decir,
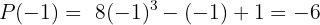
Considera el polinomio 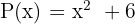 . Encuentra el residuo que resulta al dividir por
. Encuentra el residuo que resulta al dividir por 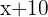
Utilizaremos el teorema del residuo
Basta con evaluar 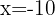 en
en  , es decir,
, es decir,
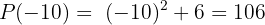
Considera el polinomio 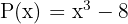 . Encuentra el residuo que resulta al dividir por
. Encuentra el residuo que resulta al dividir por 
Utilizaremos el teorema del residuo
Basta con evaluar  en
en  , es decir,
, es decir,
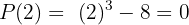
Considera el polinomio 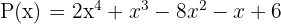 . Encuentra el residuo que resulta al dividir por:
. Encuentra el residuo que resulta al dividir por:
a 
b 
c 
d 
Utilizaremos el teorema del residuo para todos los casos:
a 
Para determinar el residuo, sólo basta con evaluar  en
en  . Es decir,
. Es decir,
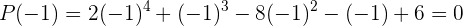
Por tanto, el residuo es 0.
b 
En este caso, debemos evaluar en  . Así,
. Así,

Así, el residuo también es 0.
c 
Ahora debemos evaluar en  . Esto es,
. Esto es,
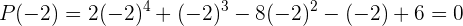
Por lo que el residuo es 0.
d 
Por último, debemos evaluar en  para encontrar el residuo en este caso. Así,
para encontrar el residuo en este caso. Así,
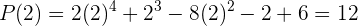
De manera que, en este último caso, el residuo es 12.
¿Eres más de aprender desde casa? Entonces, tienes que probar las clases de matematicas online de Superprof; ¡la primera es gratis!
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el cálculo con polinomios creo que la 4 estaba mal
Hola revise el ejercicio y no encontré el error, pero al principio me confundí pues la solución esta arriba del número, no se si te paso a ti, si no fue así, podrías señalármelo por favor.
HAY MUCHOS ERRORES
Miren sus soluciones a los problemas, los errores en la resolucion de sus propios problemas son DEMACIADOS.
Un ejemplo en calculos con polinomios
(x²+2)² (a+b)²=a²+2ab+b²
(x²)²+2(x²)(2)+2²
resultado real= x⁴+4x²+4
el suyo es= x⁴+2x²+4
Los invito a realizar su chequeo ya que confunde y desmotiva el uso de la pagina a la gran mayoria que estamos aprendiendo.
Hola te agradecemos tus comentarios, el error que mencionas ya se corrigió, si encuentras algún otro con gusto te atenderemos.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado