Resuelve los siguientes sistemas de ecuaciones por el método de sustitución. En caso de que alguna solución sea una fracción escríbela de la forma 
.
x=
y=
Este campo es obligatorio.
Despejamos 
de la segunda ecuación
Sustituímos el valor de en la primera ecuación:
Sustituímos el valor de 
en la segunda ecuación para calcular :
x=
y=
Este campo es obligatorio.
Quitamos paréntesis:
Despejampos 
de la segunda ecuación:
Sustituímos el valor de en la primera ecuación y despejamos :
x=
y=
Este campo es obligatorio.
Despejamos de la segunda ecuación
Sustituímos el valor de en la primera ecuación:
Sustituímos el valor de en la segunda ecuación para calcular :
x=
y=
Este campo es obligatorio.
Despejamos de la segunda ecuación
Sustituímos el valor de en la primera ecuación:
Sustituímos el valor de en la segunda ecuación para calcular :
x=
y=
Este campo es obligatorio.
Despejamos de la segunda ecuación
Sustituímos el valor de en la primera ecuación:
Sustituímos el valor de en la segunda ecuación para calcular :
x=
z=
Este campo es obligatorio.
Despejamos de la tercera ecuación
Sustituímos el valor de en la segunda ecuación:
Multiplicamos la primera ecuación por 
, sustituimos el valor 
y despejamos el valor 
:
Remplazamos el valor de y en la primera ecuación multiplicada por y obtenemos el valor de 
:
Sustituimos el valor de en y para obtener los valores de y :
Tenemos 
€ en 
monedas de 
y 
céntimos. ¿Cuántas monedas de cada clase tenemos?
Monedas de céntimos
Monedas de céntimos
Este campo es obligatorio.
En primer lugar pasamos los euros a céntimos:
€ 
céntimos.
Elegimos las incógnitas:
: número de monedas de 
céntimos.: número de monedas de 
céntimos.
Obtenemos las ecuaciones relacionando los datos.
Tenemos 
monedas, entonces 
El valor total es 
céntimos, entonces 
Antes de resolver el sistema obtenemos otro equivalente a él con el que será más fácil operar:
Resolvemos el sistema:
Despejemos 
de la primer ecuación:
Sustituyamos en la segunda ecuación y resolvamos para 
Calculamos el valor de a partir del valor de al sustituir en la primer ecuación:
Tenemos 
monedas de 50 céntimos y 
monedas de 10 céntimos.
Si no te has acordado de pasar a un sistema equivalente más sencillo recuerda que tus soluciones serán las mismas, sólo que los cálculos pueden ser un poco más complicados. Lo hacemos por una vez:
Resolvemos el sistema
Despejemos de la primer ecuación:
Sustituyamos en la segunda ecuación y resolvamos para
Calculamos el valor de a partir del valor de al sustituir en la primer ecuación:
Tenemos monedas de 50 céntimos y monedas de 10 céntimos.
Jaime va a hacer una fiesta en su casa. Va al supermercado y compra 
paquetes de patatas fritas y 
botellas de refresco de limón por 
€. Más tarde vuelve a comprar paquetes de patatas y 
botella por 
€. ¿Cuál es el precio de ambos productos?
Patatas fritas €
Botella de refresco €
Este campo es obligatorio.
Definimos las incógnitas:
: precio cada bolsa de patatas fritas.: precio de cada botella de refresco de limón.
Obtenemos las ecuaciones relacionando los datos.
En la primera compra obtenemos bolsas de patatas y botellas por 
€, por lo tanto tenemos 
.
En la segunda obtenemos de patatas y botella por €, por lo tanto obtenemos 
Resolvemos el sistema
Despejemos de la segunda ecuación:
Sustituyamos en la primera ecuación y resolvamos para 
Calculamos el valor de a partir del valor de al sustituir en la segunda ecuación:
El precio de cada bolsa de patatas es de 
€ y el de cada botella de refresco es de 
€.
Dos números suman 
y el doble de uno de ellos es 
. ¿Qué números son de menor a mayor?
Primer número
Segundo número
Este campo es obligatorio.
Definimos las incógnitas:
: primer número.: segundo número.
Obtenemos las ecuaciones relacionando los datos.
La suma de los dos números es 
, por lo tanto tenemos 
.
El doble de uno de ellos es 
, por lo tanto obtenemos 
Resolvemos el sistema
Despejemos de la segunda ecuación:
Sustituyamos en la primera ecuación y resolvamos para
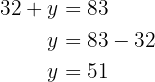
Por lo tanto los números son 
y 
.
Hallar la medida de los lados de un rectángulo cuyo perímetro es 48 y cuyo lado mayor mide el triple que su lado menor.
Lado mayor
Lado menor
Este campo es obligatorio.
Definimos las incógnitas:
: lado mayor.: lado menor.
Obtenemos las ecuaciones relacionando los datos.
El perímetro mide 
, por lo tanto tenemos 
.
El lado mayor mide tres veces el menor, por lo tanto obtenemos 
Resolvemos el sistema
Remplazamos la segunda ecuación en la primera:
Calculamos el valor de a partir del valor de al sustituir en la segunda ecuación:
El lado mayor es 
y el lado menor es 
.
En un examen, las preguntas correctas suman un punto y las incorrectas restan medio punto. En total hay 
preguntas y hay que contestar todas las preguntas. Un alumno obtuvo 
sobre . Calcular el número de preguntas que contestó de manera correcta e incorrectamente.
Respuestas correctas
Respuestas incorrectas
Este campo es obligatorio.
Definimos las incógnitas:
: respuestas correctas.: respuestas incorrectas.
Obtenemos las ecuaciones relacionando los datos.
La suma total de respuestas correctas e incorrectas es , por lo tanto tenemos 
.
La nota final es sobre pero tenemos preguntas así que debemos ajustar el valor obtenido en la prueba multiplicando por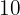 
. Dado que las respuestas correctas aportan punto y las incorrectas 
punto, obtenemos 
Resolvemos el sistema
Despejemos de la segunda ecuación:
Sustituyamos en la primera ecuación y resolvamos para
Calculamos el valor de a partir del valor de al sustituir en la segunda ecuación:
El número de respuestas correctas fue 
y el número de respuestas incorrectas fue 
.
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me encanta su contenido, realmente me ayuda pero realmente me ayudaría incluso más si dieran un poco más de referencias para citar el documento, fecha, marta ¿Qué? Bueno, ya saben lo necesario para crear APA
¡Hola Cindy! 👋 Desde Superprof nos alegra que el contenido te sea útil. 😊 Para citar el artículo en formato APA, puedes referenciarlo así:
«Superprof. Ejercicios del método de Gauss II. [En línea] Disponible en: [URL del artículo].»
Por privacidad, no podemos dar datos personales del autor ni fecha exacta de publicación, pero esta referencia permite que tu cita sea válida. 📚✨
Como puedo solucionar
Y: -3x+2
La novena esta mal, es x= 2 y= 0 , mega confirmado, grave error, en su pagina dice que la respuesta es x= 4 y= -3 lo cual no es verdad, por cualquier metodo que se haga, porfavor corregir gracias por los ejercicios de practica
Una disculpa por el error cometido, ya se corrigió.
como puedo resolver el siguiente sistema de ecuaciones
3x+4y+5z=35
2x+5y+3z=27
2x+ y+ z=13
Cómo puedo resolver la siguiente ecuación con el método Gauss – Jordan
5x-10y = 5x+20
[7x-3y=2 3x+4y=-15
I+y=5
I-y=1