Capítulos

Problemas de áreas y perímetros
¿Cuál es el área de un rectángulo sabiendo que su perímetro mide 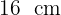 y que su base es el triple de su altura?
y que su base es el triple de su altura?
1 Establecemos las variables
 base del rectángulo
base del rectángulo
 altura del rectángulo
altura del rectángulo
2 Escribimos las ecuaciones
 perímetro
perímetro
3Formamos el sistema, en la primera ecuación se establece la realación entre la base con la altura y en la segunda el perímetro
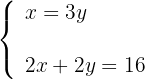
4Sustituimos el valor de  de la primera ecuación en la segunda ecuación, de modo que calculmos el valor de
de la primera ecuación en la segunda ecuación, de modo que calculmos el valor de 
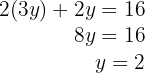
5Para hallar el valor de  sustitimos en la primera ecuación
sustitimos en la primera ecuación

6Así, la base mide  y la altura es
y la altura es 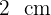
¿Cuál es el perímetro de un rectángulo sabiendo que su área mide 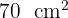 y que su base es el tres centímetros mayor que su altura?
y que su base es el tres centímetros mayor que su altura?
1 Establecemos las variables
 base del rectángulo
base del rectángulo
 altura del rectángulo
altura del rectángulo
2 Escribimos las ecuaciones
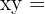 área
área
3Formamos el sistema, en la primera ecuación se establece la relación entre la base con la altura y en la segunda el área
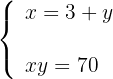
4Sustituimos el valor de  de la primera ecuación en la segunda ecuación, de modo que calculamos el valor de
de la primera ecuación en la segunda ecuación, de modo que calculamos el valor de 
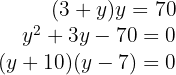
Luego 
5Para hallar el valor de  sustitimos en la primera ecuación
sustitimos en la primera ecuación
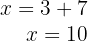
6Así, la base mide  y la altura es
y la altura es  , por lo que el perímetro es de
, por lo que el perímetro es de 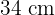
La base de un triángulo es tres unidades mayor que su altura. Si su área es 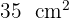 , ¿cuáles son las medidas del triángulo?
, ¿cuáles son las medidas del triángulo?
1 Establecemos las variables
 base del triángulo
base del triángulo
 altura del triángulo
altura del triángulo
2 Escribimos las ecuaciones
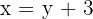
3Formamos el sistema, en la primera ecuación se establece la realación entre la base con la altura y en la segunda el área
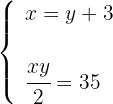
4Sustituimos el valor de  de la primera ecuación en la segunda ecuación, de modo que calculmos el valor de
de la primera ecuación en la segunda ecuación, de modo que calculmos el valor de 

luego el valor es 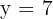 , (el valor
, (el valor  no se considera ya que no se tiene medidas negativas).
no se considera ya que no se tiene medidas negativas).
5Para hallar el valor de  sustitimos en la primera ecuación
sustitimos en la primera ecuación
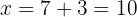
6Así, la base mide  y la altura es
y la altura es 
La base de un triángulo es el doble que su altura. Si su área es 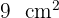 , ¿cuáles son las medidas del triángulo?
, ¿cuáles son las medidas del triángulo?
1 Establecemos las variables
 base del triángulo
base del triángulo
 altura del triángulo
altura del triángulo
2 Escribimos las ecuaciones
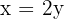
3Formamos el sistema, en la primera ecuación se establece la relación entre la base con la altura y en la segunda el área
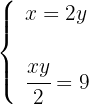
4Sustituimos el valor de  de la primera ecuación en la segunda ecuación, de modo que calculamos el valor de
de la primera ecuación en la segunda ecuación, de modo que calculamos el valor de 
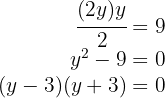
luego el valor es  , (el valor
, (el valor  no se considera ya que no se tiene medidas negativas).
no se considera ya que no se tiene medidas negativas).
5Para hallar el valor de  sustitimos en la primera ecuación
sustitimos en la primera ecuación

6Así, la base mide  y la altura es
y la altura es 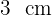
La base de un triángulo isósceles es 2 unidades mayor que su altura. Si su área es 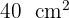 , ¿cuáles son las medidas del triángulo?
, ¿cuáles son las medidas del triángulo?
1 Establecemos las variables
 base del triángulo
base del triángulo
 altura del triángulo
altura del triángulo
2 Escribimos las ecuaciones
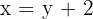
3Formamos el sistema, en la primera ecuación se establece la relación entre la base con la altura y en la segunda el área
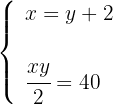
4Sustituimos el valor de  de la primera ecuación en la segunda ecuación, de modo que calculamos el valor de
de la primera ecuación en la segunda ecuación, de modo que calculamos el valor de 
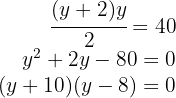
luego el valor es 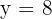 , (el valor
, (el valor  no se considera ya que no se tiene medidas negativas).
no se considera ya que no se tiene medidas negativas).
5Para hallar el valor de  sustitimos en la primera ecuación
sustitimos en la primera ecuación
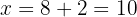
6Así, la base mide  y la altura es
y la altura es 
Problemas de la granja
Una granja tiene pavos y cerdos, en total hay  cabezas y
cabezas y 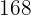 patas. ¿Cuántos cerdos y pavos hay?
patas. ¿Cuántos cerdos y pavos hay?
1 Establecemos las variables
 número de pavos
número de pavos
 número de cerdos
número de cerdos
2 Escribimos las ecuaciones, en la primera ecuación relacionamos las cabezas y en la segunda ecuación las patas
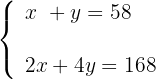
3Resolvemos el sistema por reducción, multiplicando la primera ecuación por −2

4Para hallar el valor de  sustituimos el valor de
sustituimos el valor de  en la primera ecuación
en la primera ecuación
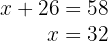
5Así, hay  pavos y
pavos y  cerdos
cerdos
Pedro y Juan tienen pavos. Juan dice: si me das  pavos, tendremos la misma cantidad; Pedro responde: si me das
pavos, tendremos la misma cantidad; Pedro responde: si me das  pavos tendría tres veces más de lo que tu tuvieras. ¿Cuántos pavos tiene cada uno?
pavos tendría tres veces más de lo que tu tuvieras. ¿Cuántos pavos tiene cada uno?
1 Establecemos las variables
 número de pavos de Pedro
número de pavos de Pedro
 número de pavos de Juan
número de pavos de Juan
2 Escribimos las ecuaciones
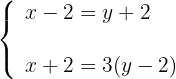
3Despejamos  en la primera ecuación y sustituimos en la segunda
en la primera ecuación y sustituimos en la segunda
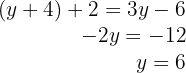
4Para hallar el valor de  sustituimos el valor de
sustituimos el valor de  en la primera ecuación
en la primera ecuación

5Así, Pedro tiene  pavos y Juan tiene
pavos y Juan tiene  pavos
pavos
María va al mercado y compra  manzanas y
manzanas y  naranjas por
naranjas por  €. Si hubiese comprado
€. Si hubiese comprado  manzanas y
manzanas y  naranjas hubiéra pagado
naranjas hubiéra pagado  €. ¿Cuál es el precio de cada fruta?
€. ¿Cuál es el precio de cada fruta?
1 Establecemos las variables
 precio de la manzana
precio de la manzana
 precio de la naranja
precio de la naranja
2Formamos el sistema

3Realizamos es sistema por reducción, multiplicando la primera ecuación por −2 y la segunda por 3
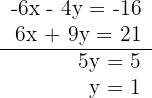
4Calculamos el valor de  sustituyendo el valor de
sustituyendo el valor de  en la primera ecuación
en la primera ecuación
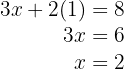
5 Así, el precio de la manzana es  € y el de la naranja es
€ y el de la naranja es  €
€
Pedro compra  peras y
peras y  mangos por
mangos por  €. Al día siguiente compra
€. Al día siguiente compra  pera y
pera y  mangos y paga
mangos y paga  €. Si en ambos días el precio de la fruta no presentó aumento ni disminución en el precio, ¿cuál es el precio de cada fruta?
€. Si en ambos días el precio de la fruta no presentó aumento ni disminución en el precio, ¿cuál es el precio de cada fruta?
1 Establecemos las variables
 precio de la pera
precio de la pera
 precio del mango
precio del mango
2Formamos el sistema
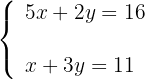
3Realizamos es sistema por reducción, multiplicando la segunda ecuación por -5
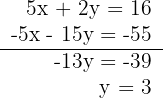
4Calculamos el valor de  sustituyendo el valor de
sustituyendo el valor de  en la segunda ecuación
en la segunda ecuación
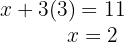
5 Así, el precio de la pera es  € y el del mango es
€ y el del mango es  €
€
En el mercado venden venden  manzanas y
manzanas y  duraznos por
duraznos por  €. También venden
€. También venden  manzanas y
manzanas y  duraznos por
duraznos por  €. ¿Cuál es el precio de cada fruta?
€. ¿Cuál es el precio de cada fruta?
1 Establecemos las variables
 precio de la manzana
precio de la manzana
 precio del durazno
precio del durazno
2Formamos el sistema
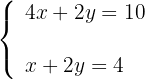
3Realizamos es sistema por reducción
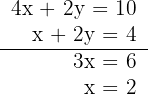
4Calculamos el valor de  sustituyendo el valor de
sustituyendo el valor de  en la primera ecuación
en la primera ecuación
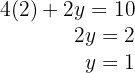
5 Así, el precio de la manzana es  € y el del durazno es
€ y el del durazno es  €
€
Problemas aritméticos
La suma de dos números es 11 y su diferencia es 7, ¿cuáles son estos números?
1 Establecemos las variables
 número mayor
número mayor
 número menor
número menor
2Formamos el sistema
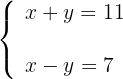
3Resolvemos el sistema por reducción
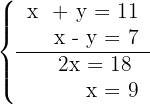
4Sustituimos el valor de  en la primera ecuación
en la primera ecuación
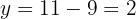
5Así, los números buscados son  y
y 
La suma de dos números es 33 y la tercera parte del mayor menos la mitad del menor es 1, ¿cuáles son estos números?
1 Establecemos las variables
 número mayor
número mayor
 número menor
número menor
2Formamos el sistema
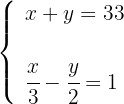
3Resolvemos el sistema por reducción, para lo cual multiplicamos por 2 la segunda ecuación
4Sustituimos el valor de  en la primera ecuación
en la primera ecuación
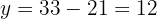
5Así, los números buscados son  y
y 
La suma de dos números es 21 y uno de ellos es igual a doble del otro, ¿cuáles son estos números?
1 Establecemos las variables
 número mayor
número mayor
 número menor
número menor
2Formamos el sistema
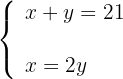
3Resolvemos el sistema por sustitución
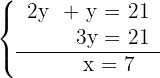
4Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
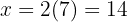
5Así, los números buscados son  y
y 
La cifra de las decenas de un número de dos cifras es el doble de la cifra de las unidades, y si a dicho número le restamos  se obtiene el número que resulta al invertir el orden de sus cifras. ¿Cuál es ese número?
se obtiene el número que resulta al invertir el orden de sus cifras. ¿Cuál es ese número?
1 Establecemos las variables
 cifra de las unidades
cifra de las unidades
 cifra de las decenas
cifra de las decenas
2 Representamos el número
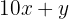
3 Representamos el número invertido
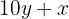
4Formamos el sistema
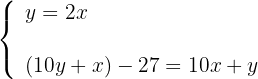
5Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación

6Resolvemos la ecuación

7Calculamos el valor de 
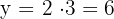
8El número buscado es 
Encuentra un número de dos cifras sabiendo que su cifra de la decena suma  con la cifra de su unidad y que si se invierte el orden de sus cifras se obtiene un número que es igual al primero menos
con la cifra de su unidad y que si se invierte el orden de sus cifras se obtiene un número que es igual al primero menos  .
.
1 Establecemos las variables
 cifra de las unidades
cifra de las unidades
 cifra de las decenas
cifra de las decenas
2 Escribimos las condiciones
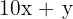 número
número
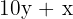 número invertido
número invertido
3Formamos el sistema

4Despejamos  en la primera ecuación y en la segunda operamos
en la primera ecuación y en la segunda operamos
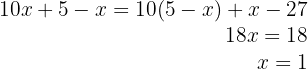
5Sustituimos el valor de  en la primera ecuación
en la primera ecuación
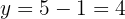
6Así, el número 
Problemas costos
Juan compró un ordenador y un televisor por  € y los vendió por
€ y los vendió por 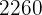 €. ¿Cuánto le costó cada objeto, sabiendo que en la venta del ordenador ganó el
€. ¿Cuánto le costó cada objeto, sabiendo que en la venta del ordenador ganó el  y en la venta del televisor ganó el
y en la venta del televisor ganó el  ?
?
1 Establecemos las variables
 precio del ordenador
precio del ordenador
 precio del televisor
precio del televisor
2 Escribimos los precios de venta
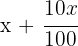
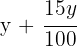
3Formamos un sistema con la ecuación de compra y otro con la ecuación de la venta
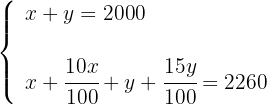
4Quitamos los denominadores
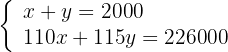
5Resolvemos el sistema por reducción, multplicando la primera ecución por −110
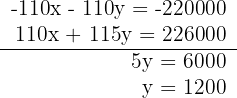
6Sustituimos el valor de la  en la primera ecuación
en la primera ecuación

Así, el precio del ordenador es 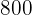 € y el precio del televisor es
€ y el precio del televisor es 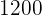 €.
€.
Antonio dice a Pedro: "el dinero que tengo es el doble del que tienes tú", y Pedro contesta: "si tú me das seis euros tendremos los dos igual cantidad". ¿Cuánto dinero tenía cada uno?
1 Establecemos las variables
 dinero de Antonio
dinero de Antonio
 dinero de Pedro
dinero de Pedro
2Formamos el sistema, en la primera ecuación expresamos lo que dice Antonio y en la segunda expresamos el comentario de Pedro, teniendo en cuenta que si da  € tendrá
€ tendrá  € menos
€ menos

3Resolvemos el sistema por sustitución, sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
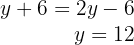
4Calculamos el valor de  en la primera ecuación
en la primera ecuación
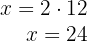
5Así, el dinero de Antonio es  € y el de Pedro es
€ y el de Pedro es  €
€
En una empresa trabajan  personas. Usan gafas el
personas. Usan gafas el  de los hombres y el
de los hombres y el  de las mujeres. Si el número total de personas que usan gafas es
de las mujeres. Si el número total de personas que usan gafas es  . ¿Cuántos hombres y mujeres hay en la empresa?
. ¿Cuántos hombres y mujeres hay en la empresa?
1 Establecemos las variables
 número de hombres
número de hombres
 número de mujeres
número de mujeres
2 Escribimos las condiciones para hombres y mujeres con gafas
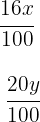
3Formamos el sistema
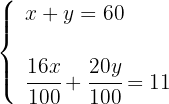
4Quitamos denominadores en la segunda ecuación
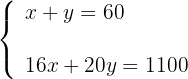
5Resolvemos el sistema por sustitución, despejando la  de la primera ecuación
de la primera ecuación
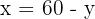
6Sustituimos la  en la segunda ecuación y resolvemos la ecuación
en la segunda ecuación y resolvemos la ecuación
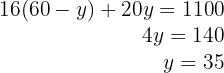
7Sustituimos el valor de  en la primera ecuación
en la primera ecuación
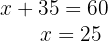
8Así, el número de hombres es  y el de mujeres es
y el de mujeres es 
Por la compra de dos electrodomésticos hemos pagado 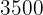 €. Si en el primero nos hubieran hecho un descuento del
€. Si en el primero nos hubieran hecho un descuento del  y en el segundo un descuento del
y en el segundo un descuento del 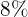 hubiéramos pagado
hubiéramos pagado 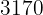 €. ¿Cuál es el precio de cada artículo?
€. ¿Cuál es el precio de cada artículo?
1 Establecemos las variables
 precio del primero
precio del primero
 precio del segundo
precio del segundo
2 Escribimos las condiciones de los descuentos
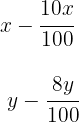
3Formamos el sistema

4Quitamos denominadores en la segunda ecuación

5Realizamos es sistema por reducción, multiplicando la primera ecuación por −90
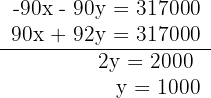
6Calculamos el valor de  sustituyendo el valor de
sustituyendo el valor de  en la primera ecuación
en la primera ecuación
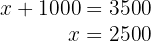
7 Así, el precio del primero es 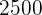 € y el segundo es
€ y el segundo es  €
€
Por la compra de dos libretas y tres lapiceros se pagaron 14 € y por la compra de una libreta y cuatro lapiceros se pagaron 12 €. ¿Cuál es el costo de cada artículo?
1 Establecemos las variables
 precio de la libreta
precio de la libreta
 precio del lapicero
precio del lapicero
2Formamos el sistema
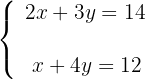
3Realizamos es sistema por reducción, multiplicando la segunda ecuación por −2
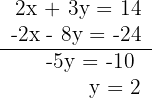
4Calculamos el valor de  sustituyendo el valor de
sustituyendo el valor de  en la segunda ecuación
en la segunda ecuación
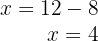
5 Así, el precio de la libreta es  € y el lapicero es
€ y el lapicero es  €
€
¿Buscas algún curso de matematicas primaria? Descubre nuestra oferta en Superprof.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Resultado de este ejercicios de sistemas de Gauss con matrices:x+y+z=3
2x+4y+z=4
3x-y+z=1
Me podrían ayudar a resolverlo
Si tengo tres rectas donde dos se superponen (hasta acá el sistema es compatible indeterminado), pero una tercer recta las cruza, es sistema se convierte es compatible determinado por haber un punto de intersección entre las tres rectas o continúa siendo compatible indeterminado por las infinitas soluciones de dos de las tres rectas?
Hola como la tercera recta intercepta a las otras dos que están superpuestas, lo hace en un solo punto, entonces solo hay una sola solución que corresponde a las tres rectas, pues para que hubiera una infinidad de puntos de respuesta las tres rectas tendrían que ser superpuestas.
en la parte del inicio no es necesario multiplicar, es mas rapido directamente si se intenta sacar el x ya que los 4y ya son capases de eliminarse entre si
Hola gracias por tu aportación lo vamos a tomar en cuenta, podrías darnos más detalles para mejorar la explicación.
El ejercicio 8 esta mal, y es 444/113, no es negativo.
Una disculpa ya se corrigió.
Una disculpa por el error, ya se corrigió.
Me encanta su contenido, realmente me ayuda pero realmente me ayudaría incluso más si dieran un poco más de referencias para citar el documento, fecha, marta ¿Qué? Bueno, ya saben lo necesario para crear APA
¡Hola Cindy! 👋 Desde Superprof nos alegra que el contenido te sea útil. 😊 Para citar el artículo en formato APA, puedes referenciarlo así:
«Superprof. Ejercicios del método de Gauss II. [En línea] Disponible en: [URL del artículo].»
Por privacidad, no podemos dar datos personales del autor ni fecha exacta de publicación, pero esta referencia permite que tu cita sea válida. 📚✨