Capítulos
¿Qué son las ecuaciones lineales?
Las ecuaciones lineales o de primer grado son del tipo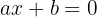 
, con 
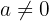, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
Pasos para resolver una ecuación lineal
En general para resolver una ecuación lineal o de primer grado debemos seguir los siguientes pasos:
1 Quitamos paréntesis
Esto es, si hay expresiones del estilo
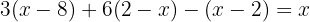
Entonces desarrollamos tomando en cuenta la propiedad distributiva, esto es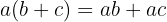 
y también la ley de los signos será importante.
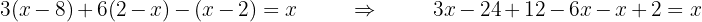
2 Quitamos denominadores
En el caso que existan términos fraccionarios en la expresión, debemos identificar los diferentes denominadores que haya, calcular el mínimo común multiplo (m.c.m) de estos y multiplicar la ecuación por el m.c.m. o en vez del m.c.m, también puedes calcular el producto de todos los denominadores aunque se recomienda más el primero, pues es un número más pequeño o más simplificado. Por ejemplo:
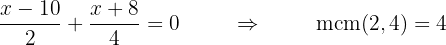
multiplicamos la primera fracción por 
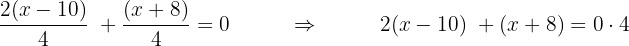
Aquí de nuevo podríamos necesitar quitar paréntesis para simplificar
3 Agrupamos los términos en x en un miembro y los términos independientes en el otro
Ya que hayamos hecho el paso 1 y paso 2, tendremos la suma y resta de términos con x y términos independientes de ambos lados de la ecuación, lo que sigue es juntar las 
de un lado y los términos independientes del otro, para esto recuerda que si de un lado de la ecuación se está sumando un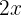 
, por ejemplo, lo puedo pasar del otro lado con la operación inversa, es decir, quedaría 
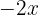del otro lado
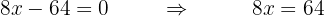
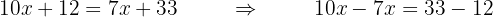
4 Reducimos los términos semejantes
Ya que tengo términos con juntos, los sumo o resto dependiendo. De igual manera con los términos independientes, por ejemplo:
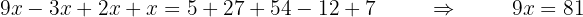
5 Despejamos la incógnita
Si hay un coeficiente acompañando a la variable , como la está multiplicando lo pasaré del otro lado con la operación inversa, esto es, dividiendo. A esto le llamo despejar
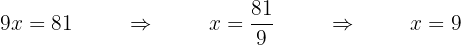
Ejercicios de ecuaciones lineales
Despejamos la incógnita, dividiendo en los dos miembros por 
. También, de manera práctica, podemos decir que el que está multiplicando en el primer miembro pasa dividiendo en el segundo.
Agrupamos los términos semejantes, tenemos que sumar en los dos miembros 
y 
, de modo que obtenemos una ecuación equivalente.
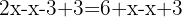
En la práctica, se suele decir que si un término está sumando en un miembro pasa al otro miembro restando 
y si estaba restando pasa al otro miembro sumando 
. Sumamos:
Utilizamos la propiedad distributiva para operar el paréntesis, es decir, multiplicar por cada termino algebraico que esta dentro del paréntesis, así del lado izquierdo tenemos: 
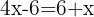
Agrupamos términos semejantes, la x que está sumando pasa al otro miembro restando y el 
que está restando pasa sumando. Sumamos:
Despejamos la incógnita, el que está multiplicando pasa al otro miembro dividiendo
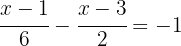
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de y
Multiplicamos ambos miembros de la ecuación por el m.c.m, en este caso , y obtenemos:
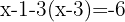
Multiplicamos usando la propiedad distributiva para resolver el paréntesis, agrupamos y sumamos los términos semejantes:
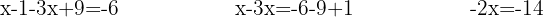
Despejamos la incógnita:
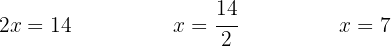
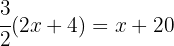
Multiplicamos 
por cada termino dentro del paréntesis (propiedad distributiva) para resolver el paréntesis y simplificamos:
Agrupamos y sumamos los términos semejantes:
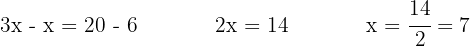
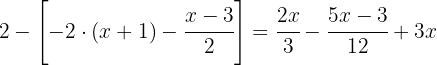
En este caso es conveniente desarrollar primero la operación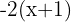 
. Al resolverla, podemos cambiar el corchete por un paréntesis.
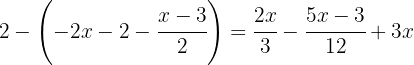
Operamos los términos dentro del paréntesis por −1 para poder quitar el signo negativo y el paréntesis de la ecuación:
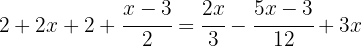
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de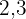 
y 
.
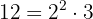
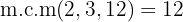
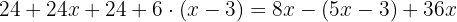
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por y el segundo por 
:
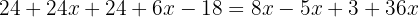
Agrupamos términos semejantes:
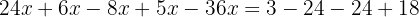
Sumamos:
Dividimos los dos miembros por: 
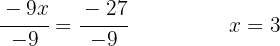
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por 
y el segundo por 
.
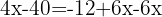
Agrupamos términos semejantes
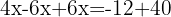
Sumamos los términos semejantes y despejamos
Usando la propiedad distributiva para resolver los paréntesis, multiplicamos el primer paréntesis por y el segundo por .
Agrupamos términos semejantes
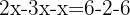
Sumamos los términos semejantes y despejamos
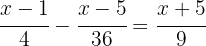
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de , 
y 
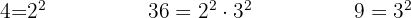
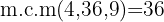
Dividimos el común denominador entre cada denominador y el resultado lo multiplicamos por el numerador correspondiente
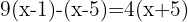
Usando la propiedad distributiva para operar los paréntesis, multiplicamos el primer por , el segundo por y el tercer por .
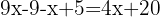
Agrupamos términos semejantes
Sumamos los términos semejantes y despejamos
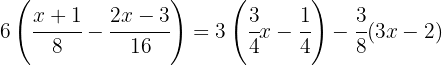
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por , el segundo por y el tercer por 
.
Es necesario recordar que cuando multiplicamos un numero entero por una fracción, se resuelve multiplicando el entero por el numerador de la fracción y el denominador queda igual.
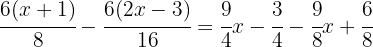
Aplicamos la propiedad distributiva para desarrollar los paréntesis en los numeradores
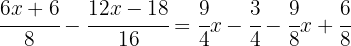
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de , 
y 
.
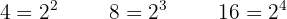
Dividimos el común denominador entre cada denominador y el resultado lo multiplicamos por el numerador correspondiente.
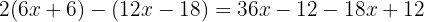
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por y simplificamos con cuidado a los cambios de signos.
Agrupamos términos semejantes
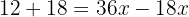
Despejamos la incógnita:
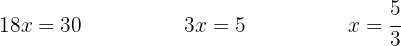
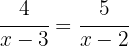
Para que se cumpla la igualdad entre las dos fracciones se tiene que cumplir que el producto de extremos sea igual al producto de medios.
O si se prefiere, también se puede hallar el m.c.m. que es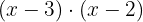 
porque los dos binomios son irreducbles. Posteriormente dividimos el m.c.m. por cada denominador y el resultado se multiplica por el numerador correspondiente.
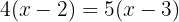
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por y el segundo por 
.
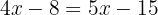
Agrupamos términos semejantes
Despejamos la incógnita:
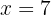
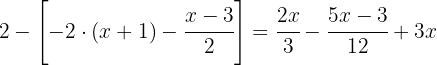
En este caso es conveniente desarrollar primero la operación 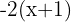. Al resolverla, podemos cambiar el corchete por un paréntesis.
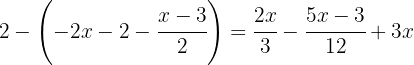
Operamos los términos dentro del paréntesis por −1 para poder quitar el signo negativo y el paréntesis de la ecuación:
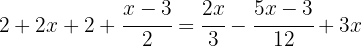
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de 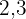y .
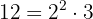
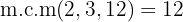
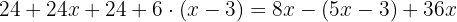
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por y el segundo por :
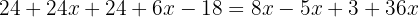
Agrupamos términos semejantes:
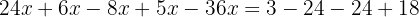
Sumamos:
Dividimos los dos miembros por:
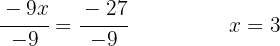
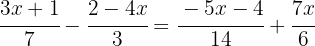
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de 
,,
y .
Dividimos el común denominador entre cada denominador y el resultado lo multiplicamos por el numerador correspondiente
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por y el segundo por 
, y el tercer por .
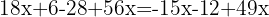
Agrupamos términos semejantes
Sumamos los términos semejantes y despejamos
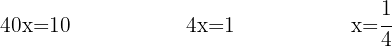
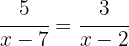
Para que se cumpla la igualdad entre las dos fracciones se tiene que cumplir que el producto de extremos sea igual al producto de medios.
O si se prefiere, también se puede hallar el m.c.m. que es 
porque los dos binomios son irreducibles. Posteriormente dividimos el m.c.m. por cada denominador y el resultado se multiplica por el numerador correspondiente.
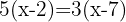
Usando la propiedad distributiva para desarrollar los paréntesis, multiplicamos el primer paréntesis por y el segundo por .
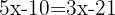
Sumamos los términos semejantes
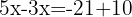
Despejamos la incógnita:
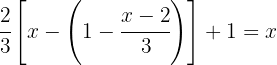
Operamos los términos dentro del paréntesis por para poder quitar el signo negativo y el paréntesis de la ecuación, ahora podemos sustituir el corchete por un paréntesis.
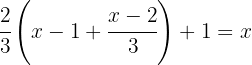
Usamos la propiedad distributiva para desarrollar los paréntesis.
Es necesario recordar que cuando multiplicamos una fracción por otra, se debe multiplicar el numerador por el numerador y el denominador por el denominador.
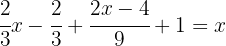
Para poder quitar los denominadores, es necesario hallar el mínimo común múltiplo de y .
Agrupamos términos semejantes:
Sumamos y despejamos:
¿Sigues teniendo dificultad? En Superprof te podemos ayudar a encontrar el mejor curso matematicas para ti.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me encanta su contenido, realmente me ayuda pero realmente me ayudaría incluso más si dieran un poco más de referencias para citar el documento, fecha, marta ¿Qué? Bueno, ya saben lo necesario para crear APA
¡Hola Cindy! 👋 Desde Superprof nos alegra que el contenido te sea útil. 😊 Para citar el artículo en formato APA, puedes referenciarlo así:
«Superprof. Ejercicios del método de Gauss II. [En línea] Disponible en: [URL del artículo].»
Por privacidad, no podemos dar datos personales del autor ni fecha exacta de publicación, pero esta referencia permite que tu cita sea válida. 📚✨
Como puedo solucionar
Y: -3x+2
La novena esta mal, es x= 2 y= 0 , mega confirmado, grave error, en su pagina dice que la respuesta es x= 4 y= -3 lo cual no es verdad, por cualquier metodo que se haga, porfavor corregir gracias por los ejercicios de practica
Una disculpa por el error cometido, ya se corrigió.
como puedo resolver el siguiente sistema de ecuaciones
3x+4y+5z=35
2x+5y+3z=27
2x+ y+ z=13
Cómo puedo resolver la siguiente ecuación con el método Gauss – Jordan
5x-10y = 5x+20
[7x-3y=2 3x+4y=-15
I+y=5
I-y=1