En un sistema de ecuaciones escalonado cada ecuación tiene una incógnita menos que la anterior. Hallar la
solución de estos sistemas es más sencillo que en el caso usual de sistema de ecuaciones. Empezamos
despejando una variable en la ultima ecuación, entonces reemplazamos ese valor en la siguiente
ecuación y así sucesivamente, al final hallamos la solución de nuestro sistema. A continuación podemos
encontrar algunos ejemplos:
1
Si nos vamos a la 3a ecuación, tenemos que 
.
Sustituyendo su valor en la 2a obtenemos que 
.
Y sustituyendo en la 1a los valores anteriores tenemos que 
.
Notemos que en este ejemplo tenemos una solución única para el sistema, no siempre es de esta forma.
2
También es un sistema escalonado:
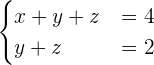
Como en este caso tenemos más incógnitas que ecuaciones, tomaremos una de las incógnitas (por ejemplo la z) y la pasaremos al segundo miembro.
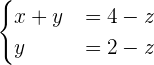
Consideraremos 
, siendo 
un parámetro que tomara cualquier valor real.
Sustituyendo en la 1ª ecuación el valor de 
en función de se tiene:
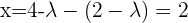
Las soluciones son:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Resultado de este ejercicios de sistemas de Gauss con matrices:x+y+z=3
2x+4y+z=4
3x-y+z=1
Me podrían ayudar a resolverlo
Si tengo tres rectas donde dos se superponen (hasta acá el sistema es compatible indeterminado), pero una tercer recta las cruza, es sistema se convierte es compatible determinado por haber un punto de intersección entre las tres rectas o continúa siendo compatible indeterminado por las infinitas soluciones de dos de las tres rectas?
Hola como la tercera recta intercepta a las otras dos que están superpuestas, lo hace en un solo punto, entonces solo hay una sola solución que corresponde a las tres rectas, pues para que hubiera una infinidad de puntos de respuesta las tres rectas tendrían que ser superpuestas.
en la parte del inicio no es necesario multiplicar, es mas rapido directamente si se intenta sacar el x ya que los 4y ya son capases de eliminarse entre si
Hola gracias por tu aportación lo vamos a tomar en cuenta, podrías darnos más detalles para mejorar la explicación.
Me encanta su contenido, realmente me ayuda pero realmente me ayudaría incluso más si dieran un poco más de referencias para citar el documento, fecha, marta ¿Qué? Bueno, ya saben lo necesario para crear APA
¡Hola Cindy! 👋 Desde Superprof nos alegra que el contenido te sea útil. 😊 Para citar el artículo en formato APA, puedes referenciarlo así:
«Superprof. Ejercicios del método de Gauss II. [En línea] Disponible en: [URL del artículo].»
Por privacidad, no podemos dar datos personales del autor ni fecha exacta de publicación, pero esta referencia permite que tu cita sea válida. 📚✨
Como puedo solucionar
Y: -3x+2