Capítulos

Método de reducción o eliminación
El método de reducción consiste en sumar o restar  ecuaciones, para obtener una tercera. Esta otra ecuación tendrá una variable menos que las anteriores, de tal manera que se pueda
ecuaciones, para obtener una tercera. Esta otra ecuación tendrá una variable menos que las anteriores, de tal manera que se pueda
despejar para encontrar la solución de una de las variables.
Ejemplo
Dado el sistema de ecuaciones siguiente:
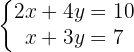
Notemos que se trata de un sistema de dos ecuaciones con dos incógnitas, podemos asumir que el sistema tiene una solución única. Entonces:
Paso 1: Verificar si ambas ecuaciones se pueden sumar o restar de tal modo, que se elimine alguna de sus variables.
De no poder eliminarse directamente, deberemos multiplicar una o las dos ecuaciones por algún valor, de tal modo que en ambas ecuaciones tengamos alguna variable con el mismo coeficiente.
Paso 2: Una vez teniendo variables con el mismo coeficiente, estas podrán restarse y así se eliminara una de las variables.
Paso 3: En la ecuación obtenida, debemos despejar la variable.
Paso 4: Sustituimos la variable en una de las dos primeras ecuaciones para obtener el valor de la otra variable.
Resolvemos:

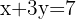
Paso 1: Como ninguna de las variables tiene el mismo coeficiente debemos de realizar una multiplicación. La segunda ecuación se debe multiplicar por  :
:

Ahora tenemos :

Paso 2: Como tenemos coeficientes iguales en una de las variables, podemos restar las ecuaciones:

Paso 3: Despejamos  .
.
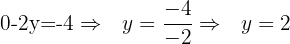
Paso 4: Sustituimos  en la primera o la segunda ecuación.
en la primera o la segunda ecuación.

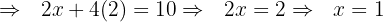
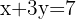

Si necesitas ayuda, también puedes encontrar el profesor matematicas perfecto para ti en Superprof.
Resolver el sistema - Coeficientes enteros
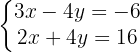
Como ambas ecuaciones tienen el mismo coeficiente en la variable  pero de signo contrario, entonces realizamos una suma de las dos ecuaciones.
pero de signo contrario, entonces realizamos una suma de las dos ecuaciones.

Despejamos la variable para encontrar su valor:
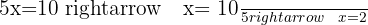
Sustituimos el valor de  en la segunda ecuación inicial.
en la segunda ecuación inicial.
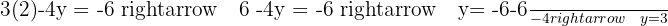
La solución es :
 y
y 
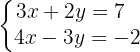
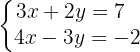
Vamos a eliminar las  , para ello multiplicamos la primera ecuación por
, para ello multiplicamos la primera ecuación por  y la segunda por
y la segunda por  .
.
Sumamos miembro a miembro y obtenemos el valor de la  .
.
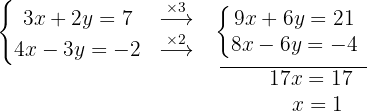
Sustituimos el valor de  en la primera ecuación inicial.
en la primera ecuación inicial.
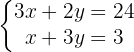
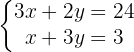
Vamos a eliminar las  , para ello multiplicamos la segunda ecuación por
, para ello multiplicamos la segunda ecuación por  .
.
Sumamos miembro a miembro y obtenemos el valor de la  .
.
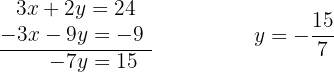
Sustituimos el valor de  en la segunda ecuación inicial.
en la segunda ecuación inicial.
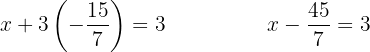
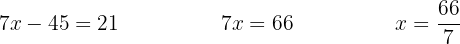
Resolver el sistema - Coeficientes racionales
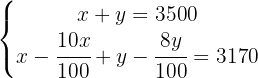
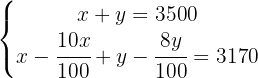
Quitamos denominadores en la segunda ecuación multiplicando a  por
por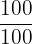 .
.
Esta fracción es igual a  , entonces no cambia la proporcionalidad de la ecuación, se trata simplemente de un truco para facilitar el cálculo.
, entonces no cambia la proporcionalidad de la ecuación, se trata simplemente de un truco para facilitar el cálculo.
Obtenemos:
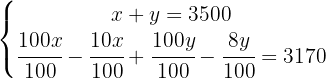
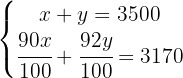
Para deshacernos de los denominadores en la segunda ecuación, multiplicamos 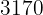 por
por  . El nuevos sistema obtenido es:
. El nuevos sistema obtenido es:
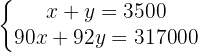
Vamos a emplear el método de reducción. Por ello, necesitamos deshacernos de una de las dos incógnitas al sumar las dos ecuaciones. Podemos entonces multiplicar la primera ecuación por 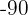 y así deshacernos de la
y así deshacernos de la  . Sumando las dos ecuaciones, obtendremos una ecuación con una incógnita (la
. Sumando las dos ecuaciones, obtendremos una ecuación con una incógnita (la  )/p>
)/p>
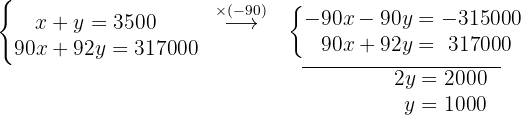
Obtenemos el valor de la 

Sustituimos el valor de  en la primera ecuación inicial
en la primera ecuación inicial

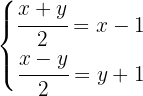
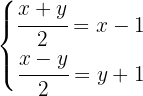
Quitamos denominadores. Para esto, multiplicamos por 2 las ecuaciones ya que en ambas solo aparece este denominador:
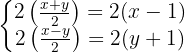
Como del lado izquierdo de las ecuaciones se está multiplicando y dividiendo por el mismo número, se cancela el 2
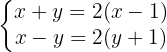
Quitamos paréntesis
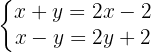
Ordenamos los términos, las variables de un lado y el término independiente del otro
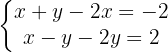
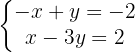
Como en las ecuaciones aparece x y -x, ya se puede hacer la reducción directamente (suma de las ecuaciones) pues se eliminará la variable x porque -x+x=0. Sumamos miembro a miembro y calculamos el valor de  .
.
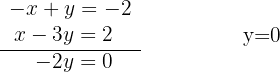
Sustituimos el valor de  en la segunda ecuación del sistema (también puedes usar la primera) y despejamos
en la segunda ecuación del sistema (también puedes usar la primera) y despejamos
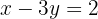


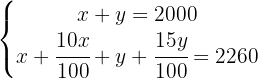
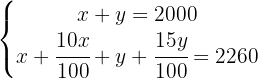
Quitamos los denominadores de la segunda ecuación multiplicando por 100, pues es el único denominador que aparece


Cancelamos el 100 en los términos donde tenga a este factor multiplicando y diviendo, pues 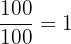
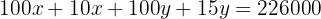
sumamos los términos similares para simplificar
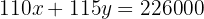
Vamos a eliminar las  , y para ello multiplicamos la primera ecuación por
, y para ello multiplicamos la primera ecuación por 
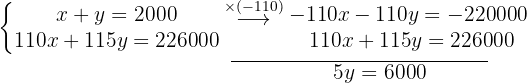
Obtenemos el valor de la  .
.
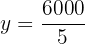

Sustituimos el valor de  en la primera ecuación y despejamos.
en la primera ecuación y despejamos.


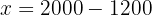
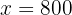
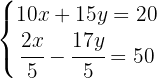
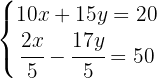
Comenzamos por quitar los denominadores de la segunda ecuación. Hacemos esto multiplicando a la segunda ecuación por 5:
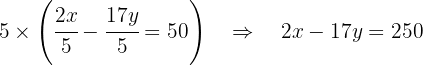
A esta última ecuación ahora la multiplicamos por -5:
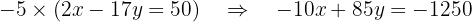
Ahora, sumamos esta ecuación con la primera para calcelar a la  :
:
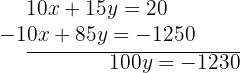
Por lo tanto, tenemos que
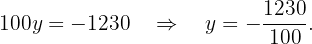
Así
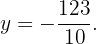
Ahora, sustituimos este valor de  en cualquiera de las 2 ecuaciones para obtener el valor de
en cualquiera de las 2 ecuaciones para obtener el valor de  . Por ejemplo, sustituimos en la primera y simplificamos
. Por ejemplo, sustituimos en la primera y simplificamos

Así, la solución al sistema de ecuaciones es
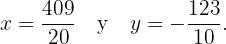
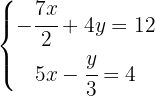
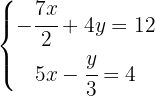
Comenzamos por quitar los denominadores de las ecuaciones. Hacemos esto multiplicando a la primera ecuación por 2 y a la segunda ecuación por 3:
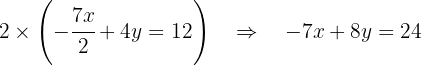
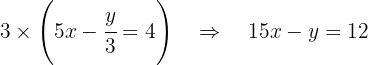
A esta última ecuación ahora la multiplicamos por 8:
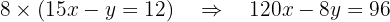
Ahora, sumamos esta ecuación con la primera para calcelar a la  :
:
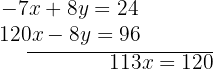
Por lo tanto, tenemos que
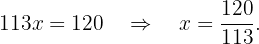
Ahora, sustituimos este valor de  en cualquiera de las 2 ecuaciones para obtener el valor de
en cualquiera de las 2 ecuaciones para obtener el valor de  . Por ejemplo, sustituimos en la primera y simplificamos
. Por ejemplo, sustituimos en la primera y simplificamos

Así, la solución al sistema de ecuaciones es
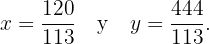
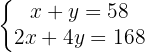
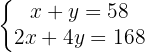
Vamos a eliminar las  multiplicando la primera ecuación por
multiplicando la primera ecuación por 
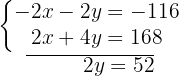
Calculamos el valor de 
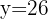
Sustituimos el valor de  en la primera ecuación.
en la primera ecuación.

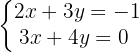
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Resultado de este ejercicios de sistemas de Gauss con matrices:x+y+z=3
2x+4y+z=4
3x-y+z=1
Me podrían ayudar a resolverlo
Si tengo tres rectas donde dos se superponen (hasta acá el sistema es compatible indeterminado), pero una tercer recta las cruza, es sistema se convierte es compatible determinado por haber un punto de intersección entre las tres rectas o continúa siendo compatible indeterminado por las infinitas soluciones de dos de las tres rectas?
Hola como la tercera recta intercepta a las otras dos que están superpuestas, lo hace en un solo punto, entonces solo hay una sola solución que corresponde a las tres rectas, pues para que hubiera una infinidad de puntos de respuesta las tres rectas tendrían que ser superpuestas.
en la parte del inicio no es necesario multiplicar, es mas rapido directamente si se intenta sacar el x ya que los 4y ya son capases de eliminarse entre si
Hola gracias por tu aportación lo vamos a tomar en cuenta, podrías darnos más detalles para mejorar la explicación.
El ejercicio 8 esta mal, y es 444/113, no es negativo.
Una disculpa ya se corrigió.
Una disculpa por el error, ya se corrigió.
Me encanta su contenido, realmente me ayuda pero realmente me ayudaría incluso más si dieran un poco más de referencias para citar el documento, fecha, marta ¿Qué? Bueno, ya saben lo necesario para crear APA
¡Hola Cindy! 👋 Desde Superprof nos alegra que el contenido te sea útil. 😊 Para citar el artículo en formato APA, puedes referenciarlo así:
«Superprof. Ejercicios del método de Gauss II. [En línea] Disponible en: [URL del artículo].»
Por privacidad, no podemos dar datos personales del autor ni fecha exacta de publicación, pero esta referencia permite que tu cita sea válida. 📚✨