Capítulos
La elipse es una curva geométrica fascinante que se encuentra en muchos aspectos de la naturaleza y las ciencias. Desde la antigüedad, matemáticos y astrónomos han estudiado y apreciado la belleza y las propiedades únicas de esta figura.
En su forma más básica, una elipse es el conjunto de todos los puntos en un plano, para los cuales la suma de las distancias a dos puntos fijos, llamados focos, es constante.

Ecuación reducida de eje horizontal de la elipse
Tomamos como centro de la elipse el centro de coordenadas y los ejes de la elipse como ejes de coordenadas. Las coordenadas de los focos son:

 y
y  . Además cualquier punto
. Además cualquier punto  sobre la elipse cumple que
sobre la elipse cumple que
 .
.
Notemos que dicha expresión es equivalente a
 .
.
Al desarrollar esta última expresión y resolviendo, tenemos que es equivalente a
 .
.
en donde  , como podemos observar en la imagen previa.
, como podemos observar en la imagen previa.
Ejemplo:Hallar los elementos característicos y la ecuación reducida de la elipse de focos:  y
y  , y su eje mayor mide
, y su eje mayor mide  .
.
Tenemos la siguiente gráfica de nuestro problema

Notemos que el centro de la elipse es el punto medio de los focos, esto es

así, el centro es el origen. Ahora, notemos que los focos están sobre el eje de las abscisas, por lo tanto, el eje mayor también lo está. También tenemos que  es la mitad del eje mayor, por lo tanto
es la mitad del eje mayor, por lo tanto 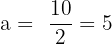 , siendo
, siendo  el semieje mayor.
el semieje mayor.
También tenemos que la mitad de la distancia focal  es la distancia de cualquiera de los focos al centro de la elipse,
es la distancia de cualquiera de los focos al centro de la elipse,  .
.
Por último, podemos encontrar el semieje menor utilizando el semieje mayor y a  , en donde el semieje menor cumple que
, en donde el semieje menor cumple que  , esto es
, esto es

de donde se sigue que  . Con esto, tenemos que la ecuación reducida de nuestra elipse es
. Con esto, tenemos que la ecuación reducida de nuestra elipse es
 .
.
Ecuación de eje horizontal de la elipse
Si el centro de la elipse  y el eje principal es paralelo al eje de las abscisas (eje
y el eje principal es paralelo al eje de las abscisas (eje  ), los focos tienen de coordenadas
), los focos tienen de coordenadas  y
y  . Y la ecuación canónica de la elipse será
. Y la ecuación canónica de la elipse será


en donde  y
y  son los semiejes mayor y menor respectivamente. Al quitar denominadores y desarrollar se obtiene, en general, una ecuación de la forma:
son los semiejes mayor y menor respectivamente. Al quitar denominadores y desarrollar se obtiene, en general, una ecuación de la forma:

Donde  y
y  tienen el mismo signo. A esta última fórmula se le conoce como ecuación general de la elipse.
tienen el mismo signo. A esta última fórmula se le conoce como ecuación general de la elipse.
Ejemplo: Hallar la ecuación canónica de la elipse de foco  , de vértice
, de vértice  y de centro
y de centro  .
.
Primero, notemos que el eje mayor es paralelo al eje de las abscisas, esto lo podemos notar gracias al centro y uno de los focos, notemos que el foco simplemente se recorre a la derecha del centro de la elipse. Esto nos da por ahora la ecuación

Ahora, sabemos que  es el semieje mayor. El semieje mayor es igual a la distancia entre el centro de la elipse y el vértice, por lo tanto
es el semieje mayor. El semieje mayor es igual a la distancia entre el centro de la elipse y el vértice, por lo tanto

Además, tenemos que el semieje menor cumple que  , en donde
, en donde  es la distancia del centro de la elipse al foco, por lo tanto
es la distancia del centro de la elipse al foco, por lo tanto

Así

Esto nos da la ecuación

Ejemplo: Hallar el centro, semiejes, vértices y focos de la elipse de ecuación

Dado que tenemos la ecuación en su forma canónica, tenemos que el centro es  .
.
Para encontrar los semiejes, tenemos que  cumple que
cumple que 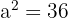 , esto es
, esto es  y, además,
y, además,  , esto es
, esto es  . Notemos que
. Notemos que  es el semieje mayor al ser más grande que
es el semieje mayor al ser más grande que  , por lo tanto
, por lo tanto  es el semieje menor.
es el semieje menor.
Ahora, notemos que dado que  representa el semieje mayor, y este divide a la expresión
representa el semieje mayor, y este divide a la expresión  entonces el eje mayor de la elipse es paralelo al eje de las abscisas, esto indica que los vértices están a
entonces el eje mayor de la elipse es paralelo al eje de las abscisas, esto indica que los vértices están a  unidades a la derecha y a
unidades a la derecha y a  unidades a la izquierda del centro, así, los vértices son
unidades a la izquierda del centro, así, los vértices son  y
y  .
.
Por último, encontremos los focos. Tenemos que la mitad de la distancia focal (la distancia del centro de la elipse a cualquier de sus focos) se denota por  y cumple que
y cumple que  , dicho esto, tenemos que
, dicho esto, tenemos que
 .
.
Así, tenemos que  y los focos son
y los focos son  y
y  .
.
Ecuación reducida de eje vertical de la elipse

Si el eje principal está sobre el eje de las ordenadas, se obtendrá la siguiente ecuación:

En donde las coordenadas de los focos son  y
y  .
.
Ejemplo: Hallar las coordenadas de los vértices, focos y la excentricidad de la elipse con ecuación reducida

Primero encontremos la mitad disstancia focal. Tenemos que la mitad de la distancia focal es  y cumple que
y cumple que  , entonces
, entonces
 ,
,
esto nos dice que  . Ahora que tenemos este valor, tenemos que los focos tienen coordenadas
. Ahora que tenemos este valor, tenemos que los focos tienen coordenadas  y
y  .
.
Para enconcontrar los vértices, recordemos que estos se encuentran a  unidades arriba y abajo del centro de la elipse, por lo tanto, dado que
unidades arriba y abajo del centro de la elipse, por lo tanto, dado que  , tenemos que los vértices son
, tenemos que los vértices son  y
y  .
.
Por último, tenemos que la excentricidad de la elipse es igual a
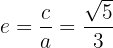 .
.
Ecuación de eje vertical de la elipse

En general, si el centro de la elipse es  (puede ser el origen o no) y el eje principal es paralelo al eje de las ordenadas (
(puede ser el origen o no) y el eje principal es paralelo al eje de las ordenadas ( ), entonces los focos tienen coordenadas
), entonces los focos tienen coordenadas  y
y  y la ecuación de la elipse será:
y la ecuación de la elipse será:

Ejercicios
Dadas las ecuaciones generales de las siguientes elipses, escríbelas en forma canónica (o reducida), obtén las coordenadas de sus focos, vértices, calcula sus excentricidades y represéntalas gráficamente.
a 
b 
c 
d 
a 
Para obtener la ecuación en su forma reducida simplemente necesitamos hacer uso de álgebra básica

Notemos que la última igualdad ya es la ecuación en su forma reducida. Dada dicha ecuación, es claro que el centro de la elipse es  .
.
Además, de la ecuación, igual tenemos que el semieje mayor es  y el semieje menor es
y el semieje menor es  . Además, como el semieje mayor divide al término de las
. Además, como el semieje mayor divide al término de las  , tenemos que el eje principal de la elipse es paralelo al eje de las abscisas. Dicho esto último, tenemos que el los vértices están a
, tenemos que el eje principal de la elipse es paralelo al eje de las abscisas. Dicho esto último, tenemos que el los vértices están a  unidades a la derecha y a la izquierda del centro de la elipse teniendo coordenadas
unidades a la derecha y a la izquierda del centro de la elipse teniendo coordenadas  y
y  .
.
Para obtener los focos, necesitamos calcular mitad de la distancia focal  la cual cumple que
la cual cumple que  , por lo tanto, tenemos que
, por lo tanto, tenemos que

Esta última igualdad nos dice que  . Ahora, los focos están a
. Ahora, los focos están a  unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas
unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas  y
y  .
.
Por último, la excentricidad está dada por

La gráfica de la elipse es la siguiente

b 
Para obtener la ecuación en su forma reducida simplemente necesitamos hacer uso de álgebra básica

Notemos que la última igualdad ya es la ecuación en su forma reducida. Dada dicha ecuación, es claro que el centro de la elipse es  .
.
Además, de la ecuación, igual tenemos que el semieje mayor es  y el semieje menor es
y el semieje menor es  . Además, como el semieje mayor divide al término de las
. Además, como el semieje mayor divide al término de las  , tenemos que el eje principal de la elipse es paralelo al eje de las ordenadas. Dicho esto último, tenemos que el los vértices están a
, tenemos que el eje principal de la elipse es paralelo al eje de las ordenadas. Dicho esto último, tenemos que el los vértices están a  unidades a arriba y abajo del centro de la elipse teniendo coordenadas
unidades a arriba y abajo del centro de la elipse teniendo coordenadas  y
y  .
.
Para obtener los focos, necesitamos calcular la mitad de la distancia focal  la cual cumple que
la cual cumple que  , por lo tanto, tenemos que
, por lo tanto, tenemos que

Esta última igualdad nos dice que  . Ahora, los focos están a
. Ahora, los focos están a  unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas
unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas  y
y  .
.
Por último, la excentricidad está dada por

La gráfica de la elipse es la siguiente

c 
Para obtener la ecuación en su forma reducida simplemente necesitamos hacer uso de álgebra básica

Notemos que la última igualdad ya es la ecuación en su forma reducida. Dada dicha ecuación, es claro que el centro de la elipse es  .
.
Además, de la ecuación, igual tenemos que el semieje mayor es  y el semieje menor es
y el semieje menor es  . Además, como el semieje mayor divide al término de las
. Además, como el semieje mayor divide al término de las  , tenemos que el eje principal de la elipse es paralelo al eje de las abscisas. Dicho esto último, tenemos que el los vértices están a
, tenemos que el eje principal de la elipse es paralelo al eje de las abscisas. Dicho esto último, tenemos que el los vértices están a  unidades a la derecha y a la izquierda del centro de la elipse teniendo coordenadas
unidades a la derecha y a la izquierda del centro de la elipse teniendo coordenadas  y
y  .
.
Para obtener los focos, necesitamos calcular la mitad de la distancia focal  la cual cumple que
la cual cumple que  , por lo tanto, tenemos que
, por lo tanto, tenemos que

Esta última igualdad nos dice que  . Ahora, los focos están a
. Ahora, los focos están a  unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas
unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas  y
y  .
.
Por último, la excentricidad está dada por

La gráfica de la elipse es la siguiente

d 
Para obtener la ecuación en su forma reducida simplemente necesitamos hacer uso de álgebra básica

Notemos que la última igualdad ya es la ecuación en su forma reducida. Dada dicha ecuación, es claro que el centro de la elipse es  .
.
Además, de la ecuación, igual tenemos que el semieje mayor es  y el semieje menor es
y el semieje menor es  . Además, como el semieje mayor divide al término de las
. Además, como el semieje mayor divide al término de las  , tenemos que el eje principal de la elipse es paralelo al eje de las ordenadas. Dicho esto último, tenemos que el los vértices están a
, tenemos que el eje principal de la elipse es paralelo al eje de las ordenadas. Dicho esto último, tenemos que el los vértices están a  unidades arriba y abajo del centro de la elipse teniendo coordenadas
unidades arriba y abajo del centro de la elipse teniendo coordenadas  y
y  .
.
Para obtener los focos, necesitamos calcular la mitad de la distancia focal  la cual cumple que
la cual cumple que  , por lo tanto, tenemos que
, por lo tanto, tenemos que

Esta última igualdad nos dice que  . Ahora, los focos están a
. Ahora, los focos están a  unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas
unidades de distancia a la izquierda y a la derecha del centro de la elipse, por lo tanto tienen coordenadas  y
y  .
.
Por último, la excentricidad está dada por

La gráfica de la elipse es la siguiente

Hallar la ecuación de la elipse conociendo los siguientes datos:
a 
b 
c 
d 
a 
Para resolver este ejercicio, primero notemos que podemos obtener fácilmente a  que es la distancia entre el foco y el centro (distancia focal), por lo tanto
que es la distancia entre el foco y el centro (distancia focal), por lo tanto  . También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto
. También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto  . Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que
. Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que  , por lo tanto
, por lo tanto

Esto último nos dice que  . Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a
. Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a  , por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a
, por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a  . Dicho todo esto, nuestra ecuación es
. Dicho todo esto, nuestra ecuación es
 .
.
b 
Para resolver este ejercicio, primero notemos que podemos obtener fácilmente a  que es la distancia entre el foco y el centro (distancia focal), por lo tanto
que es la distancia entre el foco y el centro (distancia focal), por lo tanto  . También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto
. También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto  . Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que
. Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que  , por lo tanto
, por lo tanto

Esto último nos dice que  . Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a
. Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a  , por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a
, por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a  . Dicho todo esto, nuestra ecuación es
. Dicho todo esto, nuestra ecuación es
 .
.
c 
Para resolver este ejercicio, primero notemos que podemos obtener fácilmente a  que es la distancia entre el foco y el centro (la mitad de la distancia focal), por lo tanto
que es la distancia entre el foco y el centro (la mitad de la distancia focal), por lo tanto  . También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto
. También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto  . Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que
. Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que  , por lo tanto
, por lo tanto

Esto último nos dice que  . Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a
. Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a  , por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a
, por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a  . Dicho todo esto, nuestra ecuación es
. Dicho todo esto, nuestra ecuación es
 .
.
d 
Para resolver este ejercicio, primero notemos que podemos obtener fácilmente a  que es la distancia entre el foco y el centro (media distancia focal), por lo tanto
que es la distancia entre el foco y el centro (media distancia focal), por lo tanto  . También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto
. También notemos que es sencillo obtener el semieje mayor, ya que este es la distancia entre el vértice y el centro, por lo tanto  . Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que
. Por último, tenemos que el semieje menor lo podemos determinar a partir del semieje mayor y la distancia focal, esto ya que se cumple que  , por lo tanto
, por lo tanto

Esto último nos dice que  . Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a
. Por último, recordemos que si los focos están a la derecha e izquierda del centro de la elipse, entonces el cuadrado del semieje mayor divide al término que involucra a  , por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a
, por otro lado, si los focos están por arriba o abajo del centro, entonces el cuadrado del semieje mayor divides al término que involucra a  . Dicho todo esto, nuestra ecuación es
. Dicho todo esto, nuestra ecuación es
 .
.
Escribe la ecuación reducida de la elipse cuyo centro es el origen, que pasa por el punto  y cuyo eje menor (paralelo al eje de las ordenadas) mide
y cuyo eje menor (paralelo al eje de las ordenadas) mide  .
.
El hecho de que el eje menor mida  nos dice directamente que
nos dice directamente que  . Ahora, notemos que la elipse pasa por el punto
. Ahora, notemos que la elipse pasa por el punto  , esto implica que para
, esto implica que para  y
y  se cumple la ecuación de la elipse, así, ya sustituyendo este punto y el valor de
se cumple la ecuación de la elipse, así, ya sustituyendo este punto y el valor de  , únicamente necesitamos despejar a
, únicamente necesitamos despejar a  de la ecuación y encontrar su valor,
de la ecuación y encontrar su valor,

Esto nos da la ecuación

Sabemos que una elipse tiene su centro en el origen, la mitad de su distancia focal es  . Un punto de la elipse dista de sus focos 2 y 6, respectivamente. Calcular la ecuación reducida de dicha elipse si su eje mayor esta sobre el eje de las ordenadas.
. Un punto de la elipse dista de sus focos 2 y 6, respectivamente. Calcular la ecuación reducida de dicha elipse si su eje mayor esta sobre el eje de las ordenadas.
El hecho de que la mitad de su distancia focal sea  nos dice directamente que
nos dice directamente que  , o bien
, o bien  . Ahora, sabemos que la suma de las distancias de los focos a un punto siempre es
. Ahora, sabemos que la suma de las distancias de los focos a un punto siempre es  , esto implica que
, esto implica que

Ya que tenemos a  y
y  , podemos obtener a
, podemos obtener a 

Dado que el eje mayor de la elipse está sobre el eje de las ordenadas, tenemos que la ecuación está dada por

Determina la ecuación reducida de un elipse cuya distancia focal es  y el área del rectángulo construidos sobre los ejes
y el área del rectángulo construidos sobre los ejes  . Consideremos el eje mayor de la elipse paralela al eje de las abscisas.
. Consideremos el eje mayor de la elipse paralela al eje de las abscisas.
Analicemos los datos que tenemos, primero, tenemos que la distancia focal es de  , esto implica que
, esto implica que  y, por lo tanto,
y, por lo tanto,  .
.
También tenemos que el área del rectángulo que contiene a la elipse es de  , esta área es igual al eje mayor por el eje menor de la elipse, ya que esas son las medidas del los lados del rectángulo, además, el eje mayor de la elipse mide
, esta área es igual al eje mayor por el eje menor de la elipse, ya que esas son las medidas del los lados del rectángulo, además, el eje mayor de la elipse mide  , mientras que el eje menor mide
, mientras que el eje menor mide  , esto indica que
, esto indica que  . Ahora, notemos que podemos despejar una variable en términos de la otra, en nuestro caso despejaremos
. Ahora, notemos que podemos despejar una variable en términos de la otra, en nuestro caso despejaremos  .
.
También sabemos de la relación  , pero ya tenemos el valor de
, pero ya tenemos el valor de  y a
y a  , sustituyendo estos valores en la primera igualdad podremos obtener el valor de
, sustituyendo estos valores en la primera igualdad podremos obtener el valor de  .
.

Las raíces del polinomio que encontramos son  , notemos que como
, notemos que como  debe ser real y estrictamente positivo, la única solución que lo satisface es
debe ser real y estrictamente positivo, la única solución que lo satisface es  , sustituyendo estos valores en la primera igualdad podremos obtener el valor de
, sustituyendo estos valores en la primera igualdad podremos obtener el valor de  , sustituiremos este valor en la igualdad
, sustituiremos este valor en la igualdad  para encontrar que
para encontrar que  . Ya que tenemos nuestros valores de los semiejes, procedemos a escribir la ecuación, como la elipse tiene eje mayor sobre el eje de las abscisas, tenemos que el término dividido por el cuadrado del semieje mayor es el que tiene a las
. Ya que tenemos nuestros valores de los semiejes, procedemos a escribir la ecuación, como la elipse tiene eje mayor sobre el eje de las abscisas, tenemos que el término dividido por el cuadrado del semieje mayor es el que tiene a las  , esto es
, esto es

Determina la ecuación reducida de una elipse sabiendo que uno de los vértices dista  de un foco y
de un foco y  del otro. Supongamos que la elipse tiene centro en el origen y eje mayor sobre el eje de las abscisas por simplicidad.
del otro. Supongamos que la elipse tiene centro en el origen y eje mayor sobre el eje de las abscisas por simplicidad.
La siguiente imagen nos ayudará a entender las distancias mencionadas y como, a partir de ellas, calcular  y
y  , para finalmente poder calcular
, para finalmente poder calcular  .
.

La distancia del vértice al foco más lejano es  , mientras que la distancia al más cercano es
, mientras que la distancia al más cercano es  , notemos que si a la distancia al foco más lejano le restamos la distancia al más cercano obtendremos la distancia foca, así, tendríamos que
, notemos que si a la distancia al foco más lejano le restamos la distancia al más cercano obtendremos la distancia foca, así, tendríamos que  , o bien,
, o bien,  . Por otro lado, notemos que si a la distancia del vértice al foco más lejano le sumamos la distancia al foco más cercado, obtendremos la distancia de un vértice al otro, por lo tanto, tendríamos que
. Por otro lado, notemos que si a la distancia del vértice al foco más lejano le sumamos la distancia al foco más cercado, obtendremos la distancia de un vértice al otro, por lo tanto, tendríamos que  , o bien,
, o bien,  . Una vez que tenemos estos, podemos calcular el cuadrado del semieje menor, ya que
. Una vez que tenemos estos, podemos calcular el cuadrado del semieje menor, ya que
 .
.
Así, nuestra ecuación sería
 .
.
Halla la ecuación reducida de una elipse sabiendo que pasa por el punto  y su excentricidad es
y su excentricidad es  . Supongamos que la elipse tiene centro en el origen y eje mayor sobre el eje de las abscisas por simplicidad.
. Supongamos que la elipse tiene centro en el origen y eje mayor sobre el eje de las abscisas por simplicidad.
Primero, tenemos que la excentricidad es  , despejando tenemos
, despejando tenemos  . Por otro lado, dado que pasa por el punto
. Por otro lado, dado que pasa por el punto  , tenemos que dicho punto satisface la ecuación de la elipse, esto es
, tenemos que dicho punto satisface la ecuación de la elipse, esto es

Notemos que ya tenemos el valor de  y
y  , además, sabemos que
, además, sabemos que  , sustituyamos estos valores de
, sustituyamos estos valores de  y
y  y obtengamos
y obtengamos 
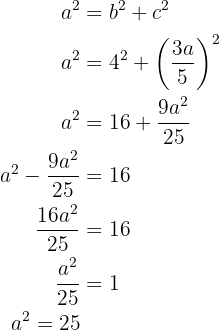
Ya podemos escribir nuestra ecuación

Escribe la ecuación de la elipse cuyo centro es  , que pasa por el punto
, que pasa por el punto  y cuyo eje mayor es (paralelo al eje de las abscisas) mide
y cuyo eje mayor es (paralelo al eje de las abscisas) mide  .
.
Como el centro no es el origen y el eje mayor es paralelo al eje de las abscisas, la ecuación es de la forma

El hecho de que el eje mayor mida  nos dice directamente que
nos dice directamente que  . Ahora, notemos que la elipse pasa por el punto
. Ahora, notemos que la elipse pasa por el punto  , esto implica que para
, esto implica que para  y
y  se cumple la ecuación de la elipse, así, ya sustituyendo este punto y el valor de
se cumple la ecuación de la elipse, así, ya sustituyendo este punto y el valor de  , únicamente necesitamos despejar a
, únicamente necesitamos despejar a  de la ecuación y encontrar su valor,
de la ecuación y encontrar su valor,

Esto nos da la ecuación

Determina la ecuación de la elipse con centro en  , distancia focal de
, distancia focal de  , eje menor paralelo al eje de las abscisas y de longitud
, eje menor paralelo al eje de las abscisas y de longitud  .
.
Como el centro no es el origen y el eje menor es paralelo al eje de las abscisas, la ecuación es de la forma

Analicemos los datos que tenemos, primero, tenemos que la distancia focal es de  , esto implica que
, esto implica que  y, por lo tanto,
y, por lo tanto,  .
.
También tenemos que la longitud del eje menor es de  , esto implica que
, esto implica que  y, por lo tanto,
y, por lo tanto, 
También sabemos de la relación  , pero ya tenemos el valor de
, pero ya tenemos el valor de  y
y  , sustituyendo estos valores en la primera igualdad podremos obtener el valor de
, sustituyendo estos valores en la primera igualdad podremos obtener el valor de  .
.

Esto nos da la ecuación

Halla la ecuación de la elipse con centro en  sabiendo que su excentricidad es
sabiendo que su excentricidad es  , su eje mayor mide
, su eje mayor mide  y es paralelo al eje de las abscisas.
y es paralelo al eje de las abscisas.
Como el centro no es el origen y el eje mayor es paralelo al eje de las abscisas, la ecuación es de la forma

Tenemos que el eje mayor mide  , esto implica que
, esto implica que  y, por lo tanto,
y, por lo tanto,  .
.
Tenemos que la excentricidad es  , despejando tenemos
, despejando tenemos  .
.
Notemos que ya tenemos el valor de  y
y  , además, sabemos que
, además, sabemos que  , sustituyamos estos valores de
, sustituyamos estos valores de  y
y  y obtengamos
y obtengamos 

Ya podemos escribir nuestra ecuación

Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5