En este artículo resolveremos ejercicios de la ecuación de la circunferencia los cuales ejemplifican cómo encontrar dicha ecuación dada información a priori de la circunferencia. Por ejemplo, dado el vértice, radio, diámetro, puntos de corte con los ejes, tangencia a los ejes, etcétera. También, trataremos los casos donde dada la ecuación de la circunferencia necesitamos extraer información precisa sobre ella como su vértice, radio, puntos de corte con los ejes, tangencia, etcétera.
Los siguientes ejercicios resueltos nos ayudarán a profundizar en los elementos de la circunferencia y pondrán a prueba nuestros conocimientos sobre ella.
Escribir la ecuación de la circunferencia de centro  y radio
y radio 
1 Sustituimos los datos en la ecuación ordinaria de la circunferencia:
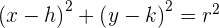
donde:
 son las coordenadas del centro y
son las coordenadas del centro y  es el radio.
es el radio.
2 Desarrollamos las potencias y obtenemos
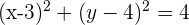
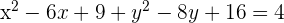
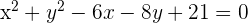
Escribir la ecuación de la circunferencia de centro 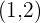 y radio
y radio 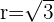
1 Sustituimos los datos en la ecuación ordinaria de la circunferencia:
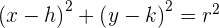
donde:
 son las coordenadas del centro y
son las coordenadas del centro y  es el radio.
es el radio.
2 Desarrollamos las potencias y obtenemos
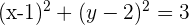
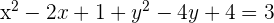
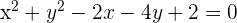
Escribir la ecuación de la circunferencia de centro 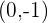 y radio
y radio 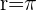
1 Sustituimos los datos en la ecuación ordinaria de la circunferencia:
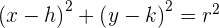
donde:
 son las coordenadas del centro y
son las coordenadas del centro y  es el radio.
es el radio.
2 Desarrollamos las potencias y obtenemos
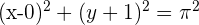
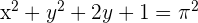
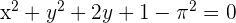
Escribir la ecuación de la circunferencia de centro  y diámetro
y diámetro 
1 Sustituimos los datos en la ecuación ordinaria de la circunferencia:
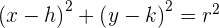
donde:
 son las coordenadas del centro y
son las coordenadas del centro y  es el radio.
es el radio.
2 Desarrollamos las potencias y obtenemos
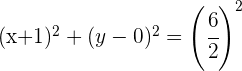
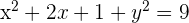
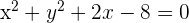
Calcula la ecuación de la circunferencia que tiene su centro en 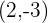 y pasa por el punto
y pasa por el punto 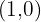
1 Sustituimos los datos en la ecuación ordinaria de la circunferencia:
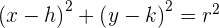
donde:
 son las coordenadas del centro y
son las coordenadas del centro y  es el radio.
es el radio.
2 Sustituimos, desarrollamos las potencias y obtenemos el radio
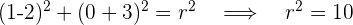
3 Sustituimos el valor del radio y del centro, desarrollamos las potencias y obtenemos
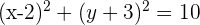
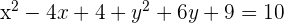
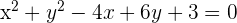
Calcula la ecuación de la circunferencia que tiene su centro en 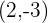 y es tangente al eje
y es tangente al eje 
1 Como la circunferencia es tangente al eje  , entonces el radio es igual a la distancia del centro al eje
, entonces el radio es igual a la distancia del centro al eje  . Luego,
. Luego, 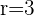
2 Sustituimos el valor del radio y del centro en la ecuación general de la circunferencia, desarrollamos las potencias y obtenemos
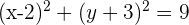
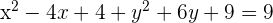
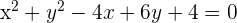
Calcula la ecuación de la circunferencia que tiene su centro en 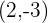 y es tangente al eje
y es tangente al eje 
1 Como la circunferencia es tangente al eje  , entonces el radio es igual a la distancia del centro al eje
, entonces el radio es igual a la distancia del centro al eje  . Luego,
. Luego, 
2 Sustituimos el valor del radio y del centro en la ecuación general de la circunferencia, desarrollamos las potencias y obtenemos
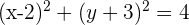
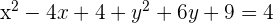
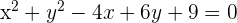
Calcula la ecuación de la circunferencia que tiene su centro en 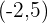 y es tangente a la recta horizontal
y es tangente a la recta horizontal 
1 Como la circunferencia es tangente a la recta  , entonces el radio es igual a la distancia del centro a dicha recta tangente. Luego,
, entonces el radio es igual a la distancia del centro a dicha recta tangente. Luego, 
2 Sustituimos el valor del radio y del centro en la ecuación general de la circunferencia, desarrollamos las potencias y obtenemos
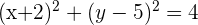
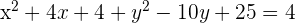
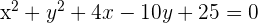
Calcula la ecuación de la circunferencia que tiene su centro en 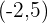 y es tangente a la recta vertical
y es tangente a la recta vertical 
1 Como la circunferencia es tangente a la recta  , entonces el radio es igual a la distancia del centro a dicha recta tangente. Luego,
, entonces el radio es igual a la distancia del centro a dicha recta tangente. Luego, 
2 Sustituimos el valor del radio y del centro en la ecuación general de la circunferencia, desarrollamos las potencias y obtenemos
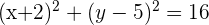
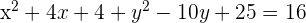
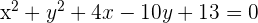
Calcula la ecuación de la circunferencia que tiene diámetro con extremos 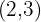 y
y 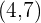
1 Como conocemos los extremos del diámetro, entonces el punto medio es el centro de la circunferencia
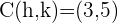
2 Para encontrar el radio, sustituimos el valor del centro y de uno de los extremos del diámetro en la ecuación general de la circunferencia
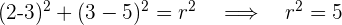
3 Sustituimos el valor del radio y del centro en la ecuación general de la circunferencia, desarrollamos las potencias y obtenemos
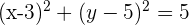
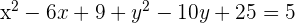
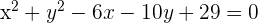
Dada la circunferencia de ecuación  , hallar el centro y el radio.
, hallar el centro y el radio.
1 Reescribimos la ecuación ordenando las  e
e  y completamos los trinomios cuadrados perfectos
y completamos los trinomios cuadrados perfectos

2 Factorizamos los trinomios cuadrados perfectos

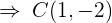 y
y 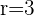
Determina las coordenadas del centro y el radio de las circunferencias:
A 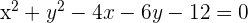
B 
C 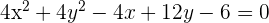
D 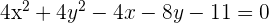
A 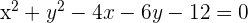 Reescribimos la ecuación en su forma ordinaria:
Reescribimos la ecuación en su forma ordinaria:
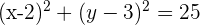
 y
y 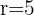
B 
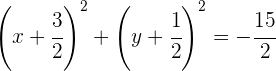 y
y 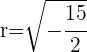
Ya que  es imaginario, no es una circunferencia real
es imaginario, no es una circunferencia real
C 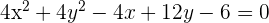
Dividiendo por 4 y reescribiendo la ecuación en forma ordinaria:
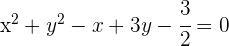
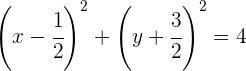
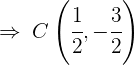 y
y 
D 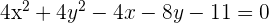
Dividiendo por 4 y reescribiendo la ecuación en forma ordinaria:
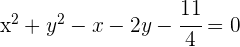
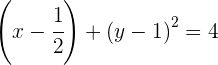
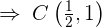 y
y 
Calcula la ecuación de la circunferencia que tiene su centro en 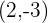 y es tangente al eje de abscisas
y es tangente al eje de abscisas
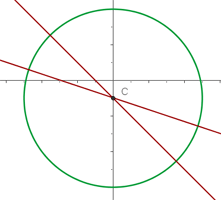
1 Graficamos la circunferencia con los datos dados:

2 A partir de la gráfica podemos deducir que
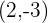

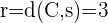
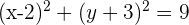
Calcula la ecuación de la circunferencia que tiene su centro en 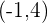 y es tangente al eje de ordenadas
y es tangente al eje de ordenadas
1 Graficamos la circunferencia con los datos dados:
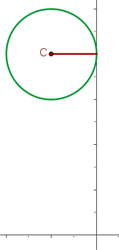
2 A partir de la gráfica podemos deducir que
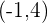
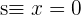
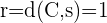

Calcula la ecuación de la circunferencia que tiene su centro en el punto de intersección de la rectas  ,
,  , y su radio es igual a
, y su radio es igual a 
1 Planteamos un sistema de ecuaciones con las rectas dadas, la solución del sistema de ecuaciones corresponde al centro de la circunferencia
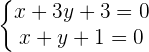

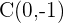
2 Sustituimos 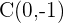 y
y 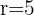 en la forma ordinaria
en la forma ordinaria
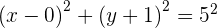
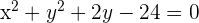
Hallar la ecuación de la circunferencia concéntrica con la ecuación  , y que pasa por el punto
, y que pasa por el punto 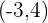
1 Por ser concéntricas tienen el mismo centro:
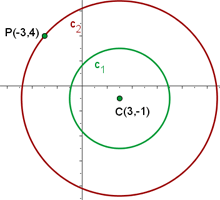
2 Calculamos el centro de la circunferencia 
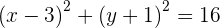
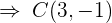
3 Para calcular el radio calculamos la distancia de 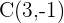 a
a 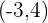

4 Sustituimos el centro y el radio en la forma ordinaria
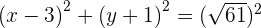

Hallar la ecuación de la circunferencia que tiene el centro en el punto 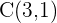 y es tangente a la recta:
y es tangente a la recta: 
1 El radio se calcula con la distancia del punto 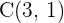 a la recta
a la recta 
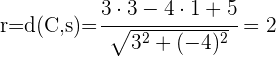
2 Sustituimos 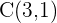 y
y  en la forma ordinaria
en la forma ordinaria
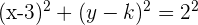
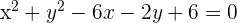

Hallar la ecuación de la circunferencia que pasa por los puntos 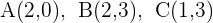
1 Considerando la ecuación general de una circunferencia como  , sustituimos los puntos dados y construimos un sistema de ecuaciones:
, sustituimos los puntos dados y construimos un sistema de ecuaciones:
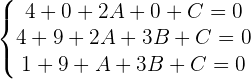
2 Resolvemos el sistema de ecuaciones y sustituimos en la forma general considerada:

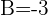
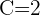

Hallar la ecuación de la circunferencia circunscrita al triángulo de vértices: 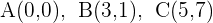
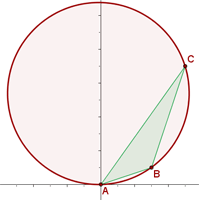
1 Considerando que los vértices del triángulo son puntos por los que pasa la circunferencia, podemos considerar la ecuación de la circunferencia como  y sustituir los puntos dados:
y sustituir los puntos dados:

2 Resolvemos el sistema de ecuaciones y sustituimos en la forma general considerada:
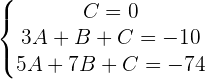
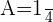

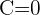
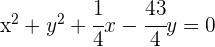
Hallar la ecuación de la circunferencia que pasa por los puntos  y
y 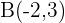 y tiene su centro sobre la recta:
y tiene su centro sobre la recta: 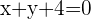
1 Consideremos que el punto  es el centro de la circunferencia y se encuentra sobre la recta
es el centro de la circunferencia y se encuentra sobre la recta 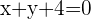 , podemos plantear el sistema:
, podemos plantear el sistema:

2 De las primeras 2 ecuaciones obtenemos:
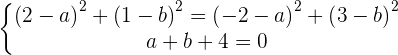
3 Resolviendo el sistema:
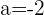

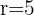
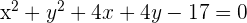
Calcula la ecuación de la circunferencia que pasa por el punto 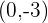 , cuyo radio es
, cuyo radio es  y cuyo centro se halla en la bisectriz del primer y tercer cuadrantes
y cuyo centro se halla en la bisectriz del primer y tercer cuadrantes

1 Consideremos que el punto  es el centro de la circunferencia, además, la bisectriz del primer y tercer cuadrante es la recta
es el centro de la circunferencia, además, la bisectriz del primer y tercer cuadrante es la recta 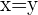 :
:



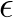

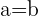

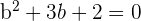
2 Obtenemos 2 soluciones para  :
:


3 Para 

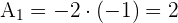
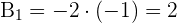
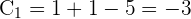
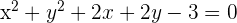
4 Para 
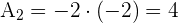
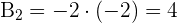
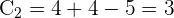
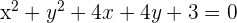
Los extremos del diámetro de una circunferencia son los puntos 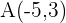 y
y  . ¿Cuál es la ecuación de esta circunferencia?
. ¿Cuál es la ecuación de esta circunferencia?
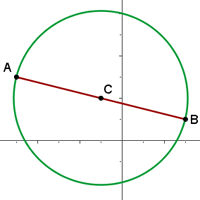
1 El radio de la circunferencia será la mitad de la distancia entre los puntos  y
y  :
:

2 El centro de la circunferencia se encontrará en el punto medio entre los puntos  y
y  :
:

3 Obtenemos los coeficientes  y
y  para la forma
para la forma 

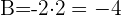
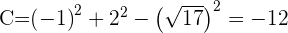

Hallar la ecuación de la circunferencia concéntrica a la circunferencia  que sea tangente a la recta
que sea tangente a la recta 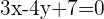
1 Obtenemos el centro de la circunferencia con coordenadas  :
:

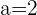
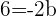
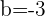
2 El radio será la distancia entre  y la recta
y la recta 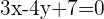 :
:
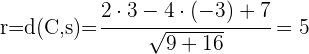
3 Obtenemos los coeficientes  y
y  para la forma
para la forma 


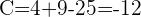
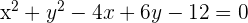
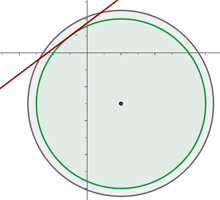
Calcula la posición relativa de la circunferencia 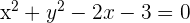 y la recta
y la recta 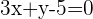
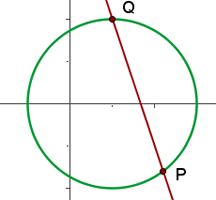
1 Planteamos un sistema de ecuaciones entre la ecuación de la circunferencia y la ecuación de la recta para buscar sus intersecciones
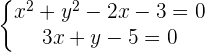
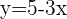
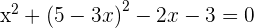
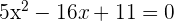

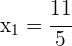
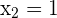
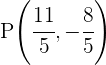

Al haber dos puntos de intersección, podemos decir que la recta y la circunferencia son secantes
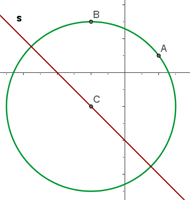
Estudiar la posición relativa de la circunferencia 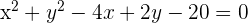 con las rectas:
con las rectas:
A 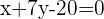
B 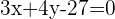
C 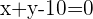
A 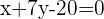
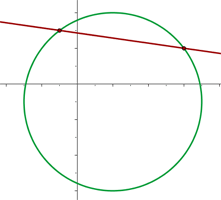
Planteamos un sistema de ecuaciones entre la ecuación de la circunferencia y la ecuación de la recta para buscar sus intersecciones:
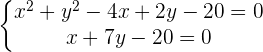

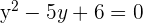
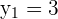

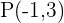

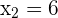
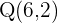
Al haber dos puntos de intersección, podemos decir que la recta y la circunferencia son secantes
B 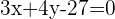
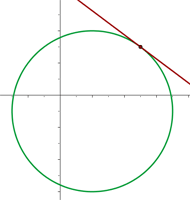
Planteamos un sistema de ecuaciones entre la ecuación de la circunferencia y la ecuación de la recta para buscar sus intersecciones:


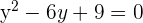



Al haber un solo punto de intersección entre la circunferencia y la recta, podemos decir que son tangentes
C 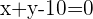
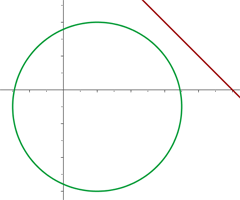
Planteamos un sistema de ecuaciones entre la ecuación de la circunferencia y la ecuación de la recta para buscar sus intersecciones:
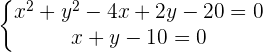
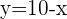

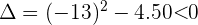
Al no existir puntos de intersección entre la recta y la circunferencia podemos decir que son exteriores
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5