
Encontrar la ecuación de la elipse
Antes de resolver los ejercicios, puedes leer el resumen sobre las propiedades de la elipse y su ecuación.
Hallar la ecuación de lugar geométrico de los puntos  cuya suma de distancias a los puntos fijos
cuya suma de distancias a los puntos fijos y
y  sea igual a
sea igual a  .
.
Buscamos que la suma de las distancias  y
y  sea siempre igual a
sea siempre igual a  , es decir,
, es decir,

Por lo tanto, tenemos que,

Si despejamos una raíz, se obtiene

Luego, elevando al cuadrado, tenemos que

Observemos que el término  se encuentra a ambos lados de la ecuación. Por tanto, podemos cancelarlo, de manera que nos queda
se encuentra a ambos lados de la ecuación. Por tanto, podemos cancelarlo, de manera que nos queda

Si expandimos los dos binomios al cuadrado, tendremos que,

Luego, reagrupando términos semejantes  dividiendo la ecuación por
dividiendo la ecuación por  —, tenemos
—, tenemos

Ya nos deshicimos de un radical. Para deshacernos del otro repetimos el procedimiento. Elevamos al cuadrado la expresión, expandemos los binomios al cuadrado y reagrupamos términos:

es decir,

Hallar la ecuación de la elipse de foco , de vértice
, de vértice  y de centro
y de centro  .
.
Sabemos que el semieje mayor es la distancia entre el centro  y el vértice
y el vértice  , es decir,
, es decir,
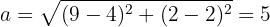
Asimismo, la semidistancia focal es la distancia entre el centro  y el foco
y el foco  de la elipse —que es la mitad de la distancia entre los dos focos—, esto es,
de la elipse —que es la mitad de la distancia entre los dos focos—, esto es,
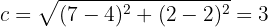
Por último, el semieje menor se calcula mediante

Así, la ecuación reducida de la elipse está dada por

Halla la ecuación de la elipse conociendo que:

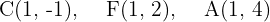
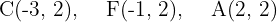

Describiremos detalladamente el primer inciso. Los demás estarán más resumidos.
Sabemos que el semieje mayor es la distancia entre el centro  y el vértice
y el vértice  , es decir,
, es decir,

Asimismo, la semidistancia focal es la distancia entre el centro  y el foco
y el foco  de la elipse —que es la mitad de la distancia entre los dos focos—, esto es,
de la elipse —que es la mitad de la distancia entre los dos focos—, esto es,
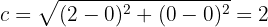
Por último, el semieje menor se calcula mediante
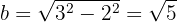
Así, la ecuación reducida de la elipse está dada por


Tenemos que,

Por tanto, el semieje menor está dado por,
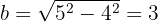
Así, la ecuación reducida de la elipse es:

Observemos que, en este caso, dividimos  por
por  en lugar de
en lugar de 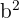 . Esto se debe a que el eje mayor es vertical (observemos que tanto
. Esto se debe a que el eje mayor es vertical (observemos que tanto  ,
,  y
y  tienen mismo valor en su coordenada
tienen mismo valor en su coordenada  ).
).
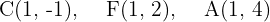
Observemos que las coordenadas  de los tres puntos es la misma. Por lo tanto, el eje mayor es vertical. Así, tenemos que
de los tres puntos es la misma. Por lo tanto, el eje mayor es vertical. Así, tenemos que

Por tanto, el semieje menor está dado por,
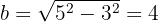
Así, la ecuación reducida de la elipse es:

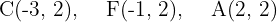
Notemos ahora que son las coordenadas  las que se encuentran fijas en cada punto. De este modo, el eje mayor de la elipse será horizontal. Así, tenemos que
las que se encuentran fijas en cada punto. De este modo, el eje mayor de la elipse será horizontal. Así, tenemos que

Además,

Por lo tanto, la ecuación reducida será

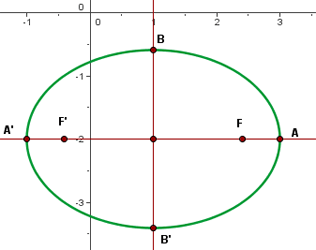
Determina la ecuación reducida de una elipse sabiendo que el eje mayor es horizontal, uno de los focos dista  de un vértice y
de un vértice y  del otro, y cuyo centro se encuentra en el origen.
del otro, y cuyo centro se encuentra en el origen.
Observa la gráfica de abajo:
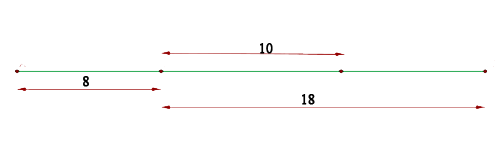
Sabemos que la distancia focal debe ser 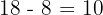 . De este modo, la semidistancia focal es,
. De este modo, la semidistancia focal es,
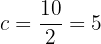
La cual es la distancia del centro a cualquier foco. De este modo, la distancia entre el centro y el vértice es
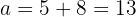
Con esto, tenemos que
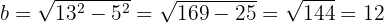
Por lo tanto, la ecuación de la elipse es

Halla la ecuación reducida de una elipse sabiendo que pasa por el punto  , tiene centro en el origen, el eje mayor es horizontal y su excentricidad es
, tiene centro en el origen, el eje mayor es horizontal y su excentricidad es 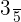 .
.
La ecuación de la elipse debe tener la forma

debido a que tiene su centro en el origen. Además, tenemos que la elipse pasa por el punto  . De este modo, se debe satisfacer que
. De este modo, se debe satisfacer que
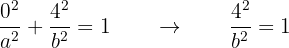
Si despejamos 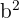 , se tiene que
, se tiene que 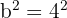 . Luego, debido a que
. Luego, debido a que 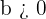 , se sigue que,
, se sigue que,

Además, en la fórmula de la excentricidad se debe cumplir que

Si elevamos al cuadrado la ecuación, se sigue que
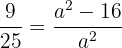
Multiplicamos la ecuación por  , y luego por
, y luego por  para obtener
para obtener
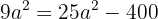
Al agrupar términos semejantes, se obtiene

Es decir,  . Por lo tanto, la ecuación de la elipse es
. Por lo tanto, la ecuación de la elipse es

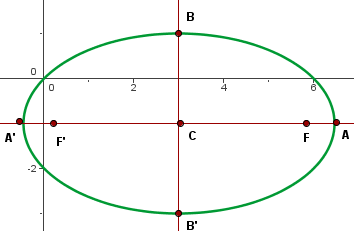
Escribe la ecuación reducida de la elipse con centro en el origen, que pasa por el punto  y cuyo eje menor mide
y cuyo eje menor mide  y este es vertical.
y este es vertical.
Como la elipse tiene centro en el origen, entonces su ecuación debe tener la forma

Además, como el eje menor mide  , entonces la semieje menor es
, entonces la semieje menor es
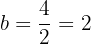
Luego, como la elipse pasa por el punto  , entonces debe satisfacer la ecuación
, entonces debe satisfacer la ecuación
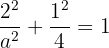
Despejando  se tiene que
se tiene que
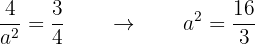
De manera que

Así, la ecuación de la elipse es
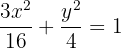
La distancia focal de una elipse con centro en el origen es  y los focos se encuentran sobre el eje x. Un punto de la elipse dista de sus focos
y los focos se encuentran sobre el eje x. Un punto de la elipse dista de sus focos  y
y  , respectivamente. Calcular la ecuación reducida de dicha elipse.
, respectivamente. Calcular la ecuación reducida de dicha elipse.
Tenemos que la distancia focal es  . Por tanto, la semidistancia focal es
. Por tanto, la semidistancia focal es
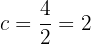
Asimismo, la suma de las distancias de cualquier punto hacia los focos siempre es constante. Esta distancia coincide con el eje mayor, de manera que

Finalmente, el semieje menor mide
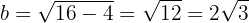
Por lo tanto, la ecuación de la elipse es
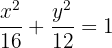
Escribe la ecuación de la elipse con centro en el origen, focos sobre el eje x, y que pasa por los puntos 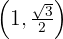 y
y 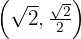 .
.
Como la elipse pasa por ambos puntos, entonces debe satisfacer el siguiente sistema de ecuaciones
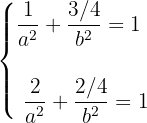
Este es un sistema no lineal con dos incógnitas (en el enlace se muestra cómo resolverlos). En este caso, utilizamos un cambio de variable

La solución de este sistema es

Para verificarlo, puedes sustituir los valores de  y
y  en el sistema no lineal original.
en el sistema no lineal original.
Por lo tanto, la ecuación de la elipse es,

Determina la ecuación de la elipse con centro en el origen, cuya distancia focal es  , focos sobre el eje x, y el área del rectángulo construido sobre los ejes es
, focos sobre el eje x, y el área del rectángulo construido sobre los ejes es  .
.
La distancia focal es  . Por lo tanto, tenemos que,
. Por lo tanto, tenemos que,

Asimismo, los semiejes menor y mayor satisfacen que —la relación que siempre cumplen  ,
,  y
y 
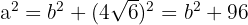
Por otro lado, tenemos un rectángulo cuyos lados miden  y
y  . Este rectángulo tiene un área dada por
. Este rectángulo tiene un área dada por

Por lo tanto, se debe resolver el siguiente sistema no lineal de ecuaciones:
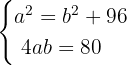
Este sistema no lineal se puede resolver despejando  de la segunda ecuación y sustituyendo su valor en la primera ecuación. Así se obtiene una ecuación bicuadrada. La solución al sistema está dada por
de la segunda ecuación y sustituyendo su valor en la primera ecuación. Así se obtiene una ecuación bicuadrada. La solución al sistema está dada por
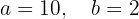
Por lo tanto, la ecuación de la elipse es

Hallar la ecuación de la elipse de foco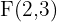 , de covértice
, de covértice 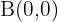 y de centro
y de centro 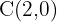 .
.
Sabemos que el semieje menor es la distancia entre el centro  y el covértice
y el covértice  , es decir,
, es decir,
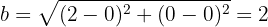
Asimismo, la semidistancia focal es la distancia entre el centro  y el foco
y el foco  de la elipse —que es la mitad de la distancia entre los dos focos—, esto es,
de la elipse —que es la mitad de la distancia entre los dos focos—, esto es,
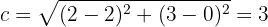
Por último, el semieje mayor se calcula mediante
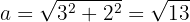
Así, la ecuación reducida de la elipse está dada por
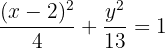
Encontrar elementos a partir de la ecuación
Hallar los elementos característicos y la ecuación reducida de la elipse de focos:  y
y 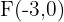 , y su eje mayor mide
, y su eje mayor mide  .
.
Hallar los elementos característicos y la ecuación reducida de la elipse de focos:  y
y 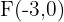 , y su eje mayor mide
, y su eje mayor mide  .
.

-
- Semieje mayor:
Tenemos que 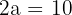 , por lo tanto, el semieje mayor es
, por lo tanto, el semieje mayor es  .
.
-
- Semidistancia focal:
Aquí tenemos que la distancia entre los dos focos es 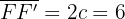 . Por lo tanto, la semidistancia focal es
. Por lo tanto, la semidistancia focal es  .
.
-
- Semieje menor:
Tenemos que  donde
donde  es el semieje menor. De este modo,
es el semieje menor. De este modo,
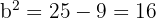
Así, el semieje menor mide  .
.
-
- Ecuación reducida:
Ya que tenemos los valores de  y
y  , así como del centro —que es el punto medio de los focos, es decir
, así como del centro —que es el punto medio de los focos, es decir  —, entonces la ecuación reducida está dada por
—, entonces la ecuación reducida está dada por

-
- Excentricidad:
Por último, la excentricidad de la elipse está dada por
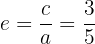
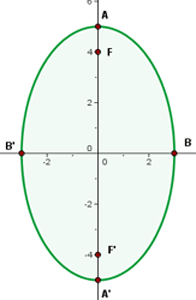
Dada la ecuación reducida de la elipse 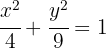 , hallar las coordenadas de los vértices, los covértices, los focos y la excentricidad.
, hallar las coordenadas de los vértices, los covértices, los focos y la excentricidad.
De la forma de la ecuación, podemos saber que la elipse tiene centro en el origen. Además, se tiene que

De este modo los vértices tienen coordenadas

ya que el eje mayor se encuentra sobre el eje  . Los covértices se encuentran en
. Los covértices se encuentran en

Asimismo, tenemos que la semidistancia focal es
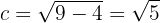
De este modo, los focos se encuentran en
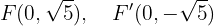
Finalmente, la excentricidad se encuentra mediante
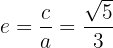
Dada la elipse de ecuación 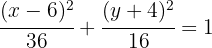 , hallar su centro, semiejes, vértices, covértices y focos.
, hallar su centro, semiejes, vértices, covértices y focos.
De la ecuación se sigue inmediatamente que el centro se encuentra en  . Asimismo, los semiejes menor y mayor son
. Asimismo, los semiejes menor y mayor son
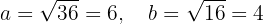
Por lo tanto,
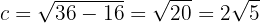
De este modo, los vértices se encuentran en 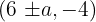 , es decir
, es decir
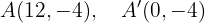
Asimismo, los focos se encuentran en

Los covértices se encuentran en los puntos
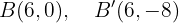
Representa gráficamente y determina las coordenadas de los focos, los vértices, los covértices y la excentricidad de las siguientes elipses.
El centro se encuentran en el origen. Los semiejes menor y mayor son

De esta manera, los vértices se encuentran en
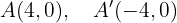
Los covértices se encuentran en los puntos
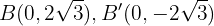
La semidistancia focal es
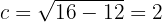
Por lo que los focos se encuentran en
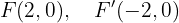
Finalmente, la excentricidad es


Primero debemos escribir la ecuación en su forma reducida, por lo que dividimos por  :
:

Luego, se la ecuación se sigue que el centro está en el origen 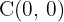 , y que
, y que

Por lo que los vértices se encuentran en
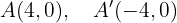
y los covértices se encuentran en

Además, la semidistancia focal es
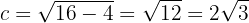
Así, los focos se encuentran en
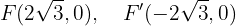
Finalmente, la excentricidad está dada por


La ecuación ya se encuentra de forma reducida. A partir de esta ecuación se puede apreciar que el centro se encuentran en 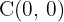 . Además, los semiejes menor y mayor están dados por
. Además, los semiejes menor y mayor están dados por
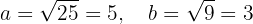
La semidistancia focal está dada por
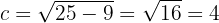
Observemos que el eje mayor está sobre el eje  . De este modo, los vértices se encuentran en
. De este modo, los vértices se encuentran en
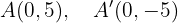
Los covértices se encuentran en,

Y los focos son los puntos,
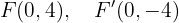
Finalmente, la excentricidad está dada por

Por último, tenemos una ecuación que no está en su forma reducida. Dividimos primero por  para obtener
para obtener
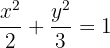
A partir de la ecuación tenemos que

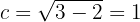
Además, observemos que el eje mayor se encuentra sobre el eje  . De este modo, los vértices se encuentran en
. De este modo, los vértices se encuentran en
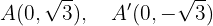
Los covértices son los puntos

Y los focos están localizados en
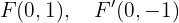
Por último, la excentricidad es
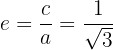

Representa gráficamente y determina las coordenadas de los focos, los vértices y los covértices de las siguientes elipses.
Para determinar los puntos importantes de la elipse, debemos escribir su ecuación de forma reducida. La forma de hacer esto es completando el cuadrado:
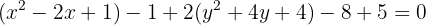
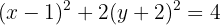
Luego, dividimos por  ,
,
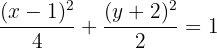
De este modo, se claro ver que el centro se encuentra en  . Además, se puede apreciar que
. Además, se puede apreciar que
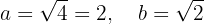
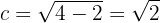
Asimismo, el eje mayor es horizontal, por lo que los vértices se encuentran en
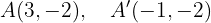
Los covértices se encuentran en

Y los focos se encuentran en

Completamos el cuadrado de nuevo:
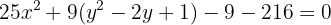

Luego, dividimos por  ,
,
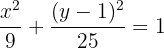
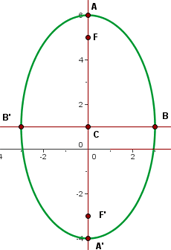
De este modo, se claro ver que el centro se encuentra en  . Además, se puede apreciar que
. Además, se puede apreciar que
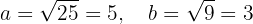
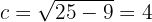
Asimismo, el eje mayor es vertical, por lo que los vértices se encuentran en
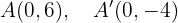
Los covértices se encuentran en
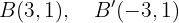
Y los focos se encuentran en

Completamos el cuadrado de nuevo:
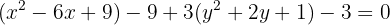
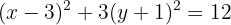
Luego, dividimos por  ,
,
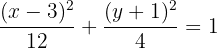
De este modo, se claro ver que el centro se encuentra en  . Además, se puede apreciar que
. Además, se puede apreciar que
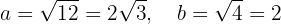

Asimismo, el eje mayor es horizontal, por lo que los vértices se encuentran en

Los covértices se encuentran en
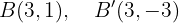
Y los focos se encuentran en

Completamos el cuadrado de nuevo:


Luego, dividimos por  ,
,
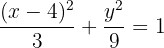
De este modo, se claro ver que el centro se encuentra en  . Además, se puede apreciar que
. Además, se puede apreciar que
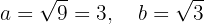
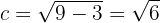
Asimismo, el eje mayor es vertical, por lo que los vértices se encuentran en

Los covértices se encuentran en

Y los focos se encuentran en
Encuentra las coordenadas del punto medio de la cuerda que intercepta la recta 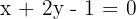 con la elipse cuya ecuación es
con la elipse cuya ecuación es 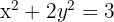 .
.
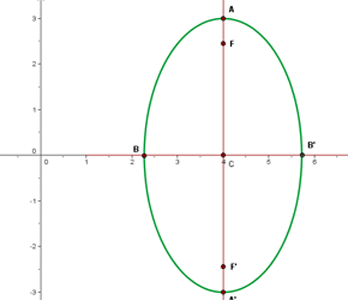
Observa primero la gráfica de la recta y la elipse:
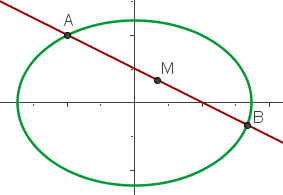
A partir de la figura podemos deducir que debemos encontrar las coordenadas de los puntos  y
y  . Luego,
. Luego,  será el punto medio de estos dos.
será el punto medio de estos dos.
Encontrar las coordenadas de  y
y  es equivalente a resolver el sistema no lineales de ecuaciones dado por
es equivalente a resolver el sistema no lineales de ecuaciones dado por
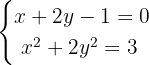
Este sistema también se resuelve por sustitución. Las soluciones están dadas por,

Por lo tanto, el punto medio de la cuerda está dado por
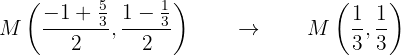
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: 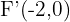 y
y 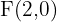 , y su eje menor mide
, y su eje menor mide  .
.
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: 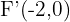 y
y 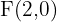 , y su eje menor mide
, y su eje menor mide  .
.
Semieje menor:
Tenemos que 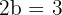 , por lo tanto, el semieje menor es
, por lo tanto, el semieje menor es 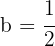 .
.
Semidistancia focal:
Aquí tenemos que la distancia entre los dos focos es 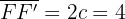 . Por lo tanto, la semidistancia focal es
. Por lo tanto, la semidistancia focal es  .
.
Semieje mayor:
Tenemos que  donde
donde  es el semieje mayor. De este modo,
es el semieje mayor. De este modo,
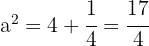
Así, el semieje mayor mide 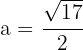 .
.
Ecuación reducida:
Ya que tenemos los valores de  y
y  , así como del centro —que es el punto medio de los focos, es decir
, así como del centro —que es el punto medio de los focos, es decir  —, entonces la ecuación reducida está dada por
—, entonces la ecuación reducida está dada por
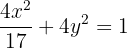
Excentricidad:
Por último, la excentricidad de la elipse está dada por
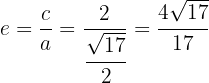
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: 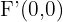 y
y 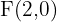 , y covértice
, y covértice 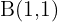 .
.
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: 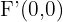 y
y 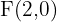 , y covértice
, y covértice 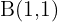 .
.
Semieje menor:
Tenemos que el centro es 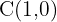 el punto medio de los focos, por lo tanto, el semieje menor es
el punto medio de los focos, por lo tanto, el semieje menor es 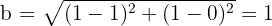 .
.
Semidistancia focal:
Aquí tenemos que la distancia entre los dos focos es 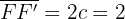 . Por lo tanto, la semidistancia focal es
. Por lo tanto, la semidistancia focal es  .
.
Semieje mayor:
Tenemos que  donde
donde  es el semieje mayor. De este modo,
es el semieje mayor. De este modo,
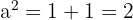
Así, el semieje mayor mide 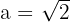 .
.
Ecuación reducida:
Ya que tenemos los valores de  y
y  , así como del centro —que es el punto medio de los focos, es decir
, así como del centro —que es el punto medio de los focos, es decir 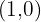 —, entonces la ecuación reducida está dada por
—, entonces la ecuación reducida está dada por
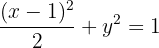
Excentricidad:
Por último, la excentricidad de la elipse está dada por
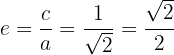
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: 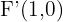 y
y 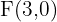 , y vértice
, y vértice 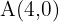 .
.
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: 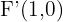 y
y 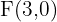 , y vértice
, y vértice 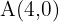 .
.
Semieje mayor:
Tenemos que el centro es 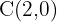 el punto medio de los focos, por lo tanto, el semieje mayor es
el punto medio de los focos, por lo tanto, el semieje mayor es 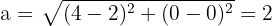 .
.
Semidistancia focal:
Aquí tenemos que la distancia entre los dos focos es 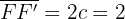 . Por lo tanto, la semidistancia focal es
. Por lo tanto, la semidistancia focal es  .
.
Semieje menor:
Tenemos que  donde
donde  es el semieje menor. De este modo,
es el semieje menor. De este modo,
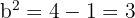
Así, el semieje menor mide  .
.
Ecuación reducida:
Ya que tenemos los valores de  y
y  , así como del centro —que es el punto medio de los focos, es decir
, así como del centro —que es el punto medio de los focos, es decir 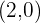 —, entonces la ecuación reducida está dada por
—, entonces la ecuación reducida está dada por
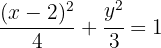
Excentricidad:
Por último, la excentricidad de la elipse está dada por
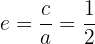
Hallar los elementos característicos y la ecuación reducida de la elipse de foco 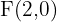 , centro
, centro 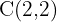 , y vértice
, y vértice 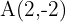 .
.
Hallar los elementos característicos y la ecuación reducida de la elipse de foco 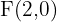 , centro
, centro 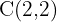 , y vértice
, y vértice 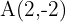 .
.
Semieje mayor:
Tenemos que el centro es 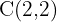 , por lo tanto, el semieje mayor es
, por lo tanto, el semieje mayor es 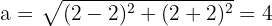 .
.
Semidistancia focal:
Aquí tenemos que la distancia del centro al foco es 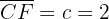 .
.
Semieje menor:
Tenemos que  donde
donde  es el semieje menor. De este modo,
es el semieje menor. De este modo,
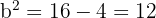
Así, el semieje menor mide 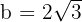 .
.
Ecuación reducida:
Ya que tenemos los valores de  y
y  , así como del centro, entonces la ecuación reducida está dada por
, así como del centro, entonces la ecuación reducida está dada por
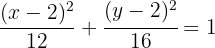
Excentricidad:
Por último, la excentricidad de la elipse está dada por
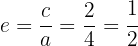
Resumir con IA:










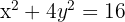
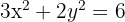

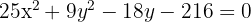





Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5