La descripción algebraica de la circunferencia esa dada por las siguientes ecuaciones
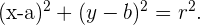
Equivalentemente
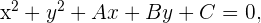
donde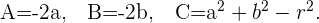 
Ecuación reducida de la circunferencia
Nos referimos a ecuación reducida de la circunferencia cuando el centro de la circunferencia coincide con el origen de coordenadas, de esta forma obtenemos la siguiente ecuación reducida
Para que una expresión del tipo: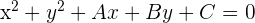 
sea una circunferencia debe cumplir que:
1 Los coeficientes de 
e 
son iguales a la unidad. Si tuvieran ambos un mismo coeficiente distinto de 1, podríamos dividir por él todos los términos.
2 No tenga término en 
.
3 Que satisfaga 
Ejemplo
Consideremos las siguientes circunferencias de radio 
y 
respectivamente, con centro el origen y en 
. Como ecuaciones obtenemos lo siguiente.
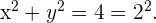
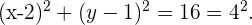
Podemos notar que la primera es una ecuación reducida de la circunferencia y la segunda tiene los siguientes parámetros 
Intersección de una cónica y una recta
Para hallar los puntos comunes a una cónica y una recta resolveremos el sistema formado por las ecuaciones de ambas.
En general se obtiene un ecuación de segundo grado, que tendrá dependiendo del signo del discrimínante,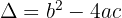 
, las siguientes soluciones:
1 Si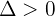 
Dos soluciones: la recta y la cónica son secantes.
2 Si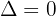 
Una solución: la recta y la cónica son tangentes.
3 Si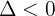 
Ninguna solución: la recta y la cónica son exteriores.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5