
Los/las mejores profesores/as de Matemáticas que están disponibles
Fórmulas de la ecuación de la hipérbola
Empezaremos estudiando los elementos que componen a la hipérbola
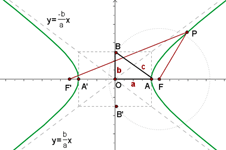
Primero notemos que la diferencia de las distancias de un punto de la hipérbola a
los focos de la hipérbola es
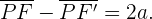
También del triángulo rectángulo formado por los punto  ,
,  y el origen
y el origen  , se tiene que
, se tiene que
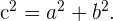
De lo anterior obtenemos los parámetros de la hipérbola usando las magnitudes  ,
,  y
y  .
.
1 Excentricidad
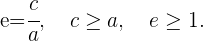
2 Asíntotas
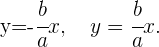
3 Ecuación reducida de la hipérbola
F'(-c,0) y F(c,0)
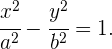
4 Ecuación de la hipérbola con los focos en el eje OY
F'(0, -c) y F(0, c)
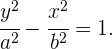
5 Ecuación de la hipérbola con eje paralelo a OX, y centro distinto al origen
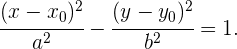
Más general dicha ecuación se ve de la siguiente manera,
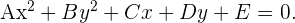
Donde  y
y  tienen signos opuestos.
tienen signos opuestos.
6 Ecuación de la hipérbola con eje paralelo a OY, y centro distinto al origen
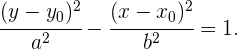
Ecuación de la hipérbola equilátera
En el caso equilátero tenemos que 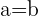 y por lo tanto la ecuación esta dada por
y por lo tanto la ecuación esta dada por
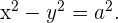
Y sus parámetros estan dados por
1 Asíntotas

2 Excentricidad
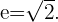
3 Ecuación de la hipérbola equilátera referida a sus asíntotas
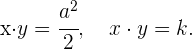
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5