Capítulos
- Ecuación reducida de la hipérbola centrada en el origen con eje real horizontal
- Ecuación reducida de la hipérbola centrada en el origen con eje real vertical
- Ecuación reducida de la hipérbola no centrada en el orige con eje real horizontal
- Ecuación reducida de la hipérbola no centrada en el orige con eje real vertical
En este artículo veremos distintas ecuaciones de la hipérbola y cómo obtenerlas.

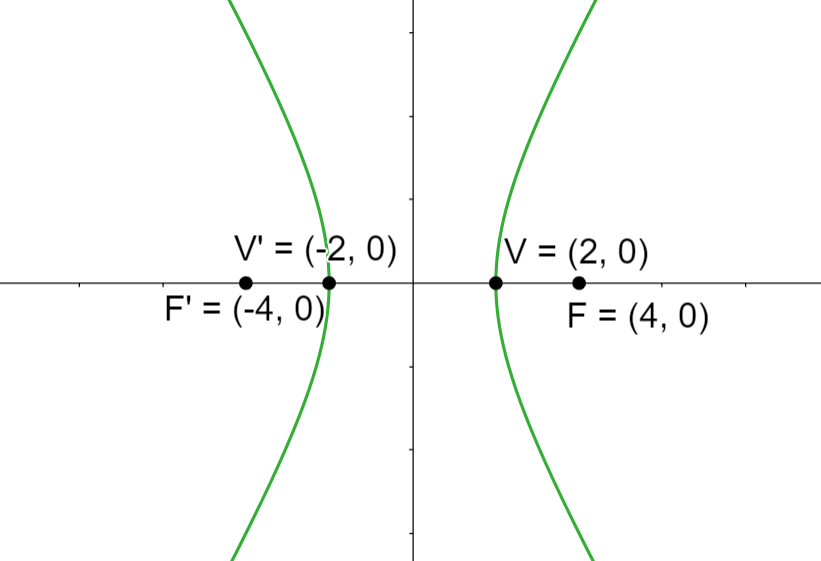
Ecuación reducida de la hipérbola centrada en el origen con eje real horizontal
Se llama ecuación reducida a la ecuación de la hipérbola cuyos ejes coinciden con los ejes coordenados, y, por tanto, el centro de hipérbola con el origen del plano. En este caso consideraremos el eje real sobre el eje de las abscisas.
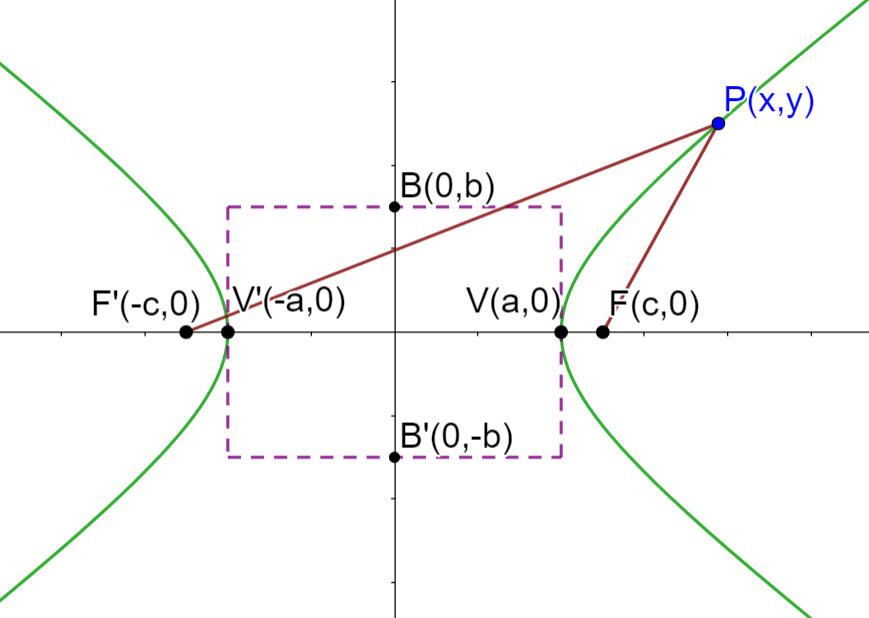
Analicemos las partes de la hipérbola que se muestran en la imagen y algunas propiedades:
1 El centro es el origen 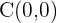 . El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
. El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
2 Vértices: Los vértices están dados por los puntos 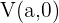 y
y  . Cada vértice está a la misma distancia del centro,
. Cada vértice está a la misma distancia del centro,  unidades.
unidades.
3 Focos: Los focos está dados por los puntos 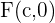 y
y 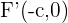 . Cada foco está a la misma distancia del centro,
. Cada foco está a la misma distancia del centro,  unidades.
unidades.
4 Eje real: Es el segmento de recta que une los vértices, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje está sobre el eje de las abscisas.
. Este eje está sobre el eje de las abscisas.
5 Eje imaginario: Es el segmento de recta que une los puntos  y
y  , esto es
, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje está sobre el eje de las ordenadas.
. Este eje está sobre el eje de las ordenadas.
6 Eje focal: Eje imaginario: Es el segmento de recta que une los focos, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  .
.
7 Las constantes  ,
,  y
y  , que definen completamente la hipérbola, satisfacen que
, que definen completamente la hipérbola, satisfacen que
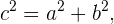
8 La excentricidad de la hipérbola está dada por
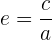
Cada punto,  , sobre la hipérbola debe cumplir que
, sobre la hipérbola debe cumplir que
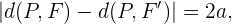
por la definición de distancia euclideana entre dos puntos, tenemos que esto es igual a
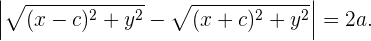
Realizando ciertas operaciones algebraicas podemos escribir la igualdad anterior de la siguiente manera
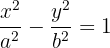
esta última ecuación se conoce como la ecuación reducida de la hipérbola con eje horizontal.
Ejercicios
A continuación veremos algunos ejercicios para poner en práctica nuestro entendimiendo de la ecuación reducida de una hipérbola.
Hallar la ecuación de la hipérbola con foco 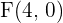 , vértice
, vértice 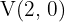 y centro
y centro 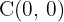
Primero, como el centro es el origen 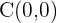 y un foco es
y un foco es  tenemos que
tenemos que  , además, sabemos que ambos focos están a
, además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es 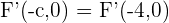 .
.
Siguiendo la misma analogía que con el foco, sabemos un vértice es 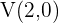 , por lo tanto
, por lo tanto  , como ambos vértices están a
, como ambos vértices están a  unidades del centro, el otro vértice es
unidades del centro, el otro vértice es 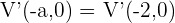 .
.
Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
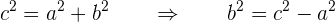
esto es
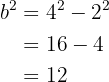
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
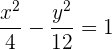
Hallar la ecuación y la excentricidad de la hipérbola que tiene como focos los puntos 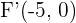 y
y 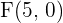 , y un eje real con valor de
, y un eje real con valor de 
Ya tenemos los focos 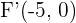 y
y 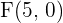 , de aquí se sigue que
, de aquí se sigue que  . Además, notemos también que el centro es el origen
. Además, notemos también que el centro es el origen 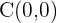 .
.
El eje real es igual a  , usaremos esto y despejaremos el valor de
, usaremos esto y despejaremos el valor de 
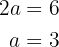
de donde se sigue inmediatamente que los vértices están dados por

Ahora, usaremos la propiedad  para obtener a el valor de
para obtener a el valor de  . Notemos que
. Notemos que
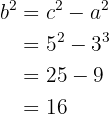
de donde se sigue inmediatamente que  . Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
. Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
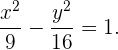
Además la excentricidad es
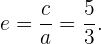
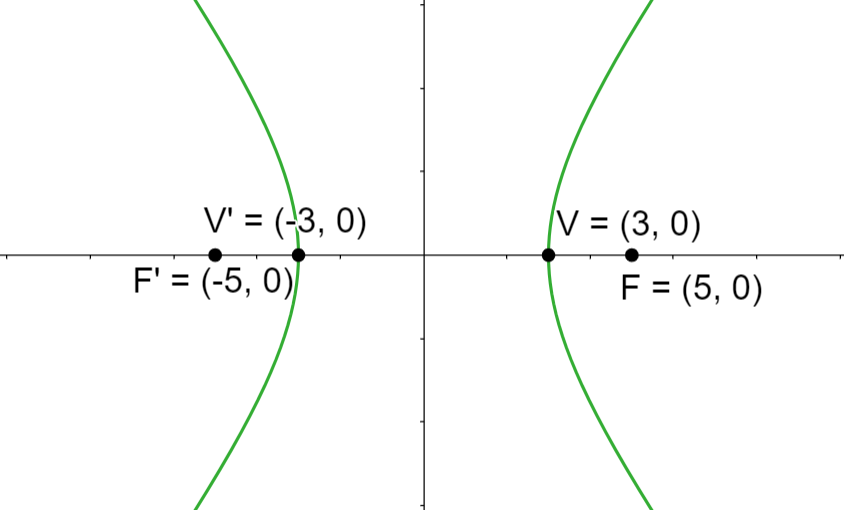
Hallar los vértices, los focos y la excentricidad de la hipérbola dada por la siguiente ecuación:
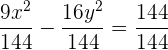
Para proceder, primero simplificaremos la ecuación a su foroma reducida
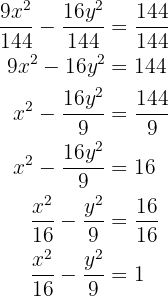
de aquí se sigue inmediatamente que 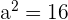 , por lo tanto
, por lo tanto 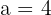 . Esto nos dice que los vértices son
. Esto nos dice que los vértices son 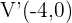 y
y 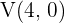 .
.
De la ecuación reducida también tenemos que  , esto implica que
, esto implica que  . De aquí ya tenemos
. De aquí ya tenemos  y
y  , entonces, recordemos que
, entonces, recordemos que
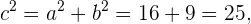
de aquí se sigue que  . Así los focos son
. Así los focos son 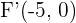 y
y 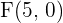 .
.
Por último, tenemos que la excentricidad está dada por
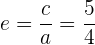
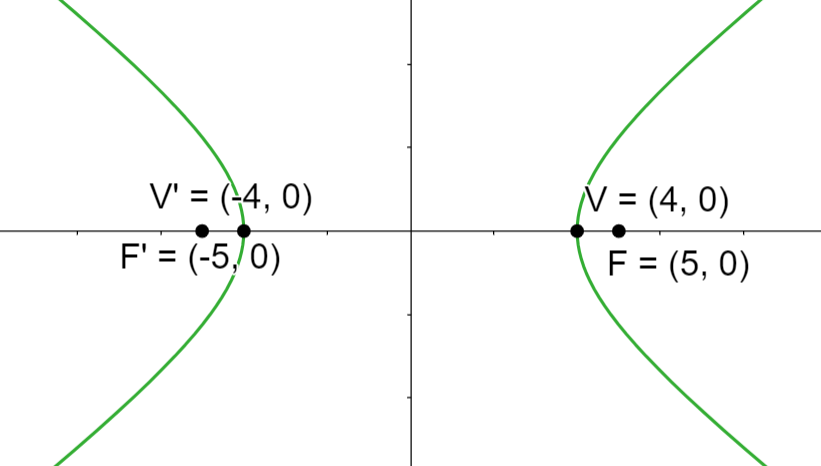
Hallar la ecuación de la hipérbola con centro 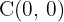 , foco
, foco  y eje imaginario igual a
y eje imaginario igual a 
Primero, como el centro es el origen 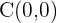 y un foco es
y un foco es  tenemos que
tenemos que  , además, sabemos que ambos focos están a
, además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es 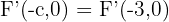 .
.
Ahora, notemos que el eje real está sobre la recta que une los focos. Esto implica que el eje real es horizontal, por lo tanto el eje imaginario es vertical. Además, tenemos que el eje imaginario tiene un valor de  , esto es
, esto es

Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
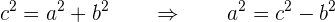
esto es
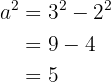
entonces  .
.
Ahora, sabemos que los vértices están a  unidades del centro, y como el eje real es horizontal, tenemos que los vértices están dados por
unidades del centro, y como el eje real es horizontal, tenemos que los vértices están dados por 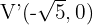 y
y 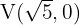 .
.
Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
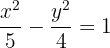
Hallar la ecuación de la hipérbola con centro 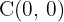 , eje focal horizontal con valor de
, eje focal horizontal con valor de  y eje imaginario vertical con valor de
y eje imaginario vertical con valor de 
Tenemos que el eje focal tiene un valor de  , de aquí obtendremos el valor de
, de aquí obtendremos el valor de 

por lo tanto los focos son 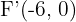 y
y 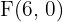 .
.
Ahora, tenemos que el eje imaginario tiene un valor de  , por lo tanto
, por lo tanto

de aquí podemos obtener  ya que
ya que
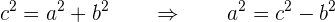
esto es
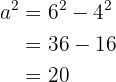
entonces 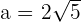 . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
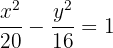
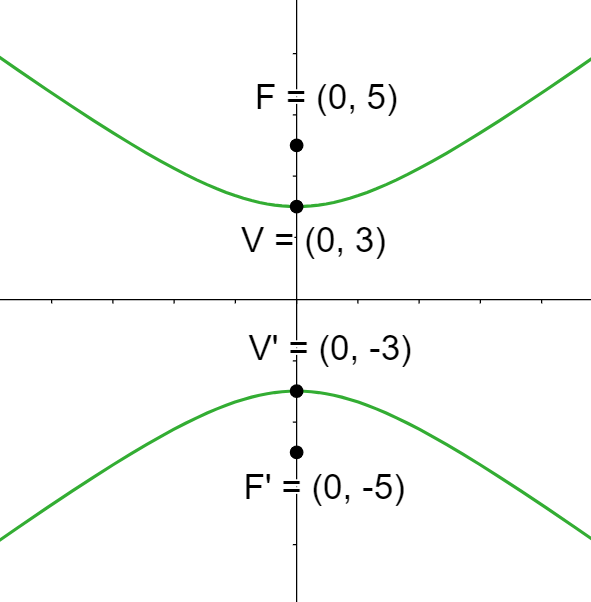
Ecuación reducida de la hipérbola centrada en el origen con eje real vertical
En este caso consideraremos el eje real sobre el eje de las ordenadas.

Analicemos las partes de la hipérbola que se muestran en la imagen y algunas propiedades:
1 El centro es el origen 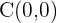 . El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
. El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
2 Vértices: Los vértices están dados por los puntos  y
y 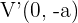 . Cada vértice está a la misma distancia del centro,
. Cada vértice está a la misma distancia del centro,  unidades.
unidades.
3 Focos: Los focos está dados por los puntos  y
y  . Cada foco está a la misma distancia del centro,
. Cada foco está a la misma distancia del centro,  unidades.
unidades.
4 Eje real: Es el segmento de recta que une los vértices, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje está sobre el eje de las ordenadas.
. Este eje está sobre el eje de las ordenadas.
5 Eje imaginario: Es el segmento de recta que une los puntos  y
y  , esto es
, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje está sobre el eje de las abscisas.
. Este eje está sobre el eje de las abscisas.
6 Eje focal: Eje imaginario: Es el segmento de recta que une los focos, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  .
.
7 Las constantes  ,
,  y
y  , que definen completamente la hipérbola, satisfacen que
, que definen completamente la hipérbola, satisfacen que
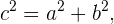
8 La excentricidad de la hipérbola está dada por
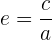
Cada punto,  , sobre la hipérbola debe cumplir que
, sobre la hipérbola debe cumplir que
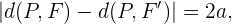
por la definición de distancia euclideana entre dos puntos, tenemos que esto es igual a
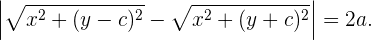
Realizando ciertas operaciones algebraicas podemos escribir la igualdad anterior de la siguiente manera
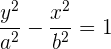
esta última ecuación se conoce como la ecuación reducida de la hipérbola con eje vertical.
Ejercicios
A continuación veremos un ejercicio para poner a prueba nuestro entendimiento.
Hallar la ecuación de la hipérbola con foco  , vértice
, vértice  y centro
y centro 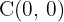
Primero, como el centro es el origen 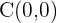 y un foco es
y un foco es  tenemos que
tenemos que  , además, sabemos que ambos focos están a
, además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es 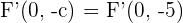 .
.
Siguiendo la misma analogía que con el foco, sabemos un vértice es  , por lo tanto
, por lo tanto  , como ambos vértices están a
, como ambos vértices están a  unidades del centro, el otro vértice es
unidades del centro, el otro vértice es 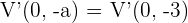 .
.
Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
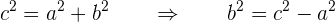
esto es
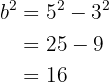
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
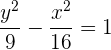
Hallar la ecuación de la hipérbola con centro 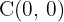 , foco
, foco  y eje imaginario igual a
y eje imaginario igual a 
Primero, como el centro es el origen 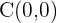 y un foco es
y un foco es  tenemos que
tenemos que  , además, sabemos que ambos focos están a
, además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es  .
.
Ahora, notemos que el eje real está sobre la recta que une los focos. Esto implica que el eje real es vertical, por lo tanto el eje imaginario es vertical. Además, tenemos que el eje imaginario tiene un valor de  , esto es
, esto es

Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
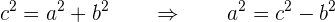
esto es
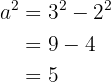
entonces  .
.
Ahora, sabemos que los vértices están a  unidades del centro, y como el eje real es vertical, tenemos que los vértices están dados por
unidades del centro, y como el eje real es vertical, tenemos que los vértices están dados por 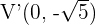 y
y 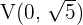 .
.
Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
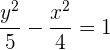
Hallar la ecuación y la excentricidad de la hipérbola que tiene como focos los puntos 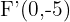 y
y 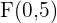 , y un eje real con valor de
, y un eje real con valor de 
Ya tenemos los focos 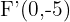 y
y 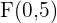 , de aquí se sigue que
, de aquí se sigue que  . Además, notemos también que el centro es el origen
. Además, notemos también que el centro es el origen 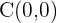 .
.
El eje real es igual a  , usaremos esto y despejaremos el valor de
, usaremos esto y despejaremos el valor de 
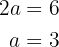
de donde se sigue inmediatamente que los vértices están dados por
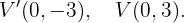
Ahora, usaremos la propiedad  para obtener a el valor de
para obtener a el valor de  . Notemos que
. Notemos que
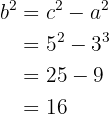
de donde se sigue inmediatamente que  . Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
. Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
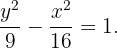
Además la excentricidad es
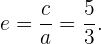
Hallar la ecuación de la hipérbola con centro 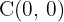 , eje focal vertical con valor de
, eje focal vertical con valor de  y eje imaginario horizontal con valor de
y eje imaginario horizontal con valor de 
Tenemos que el eje focal tiene un valor de  , de aquí obtendremos el valor de
, de aquí obtendremos el valor de 

por lo tanto los focos son 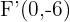 y
y 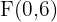 .
.
Ahora, tenemos que el eje imaginario tiene un valor de  , por lo tanto
, por lo tanto

de aquí podemos obtener  ya que
ya que
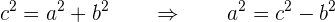
esto es
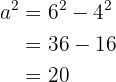
entonces 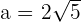 . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
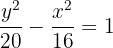
Hallar la ecuación de la hipérbola que tiene como vértices los puntos 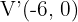 y
y 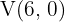 , y un eje imaginario con valor de
, y un eje imaginario con valor de 
Ya tenemos los vértices 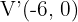 y
y 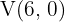 , de aquí se sigue que
, de aquí se sigue que  . Además, notemos también que el centro es el origen
. Además, notemos también que el centro es el origen 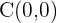 .
.
El eje imaginario es igual a  , usaremos esto y despejaremos el valor de
, usaremos esto y despejaremos el valor de 
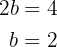
Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
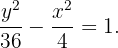
Ecuación reducida de la hipérbola no centrada en el orige con eje real horizontal
En este caso el centro de la hipérbola no es el origen y su eje real es horizontal, paralelo al eje de las abscisas.

Analicemos las partes de la hipérbola que se muestran en la imagen y algunas propiedades:
1 El centro es el origen  . El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
. El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
2 Vértices: Los vértices están dados por los puntos 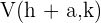 y
y 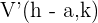 . Cada vértice está a la misma distancia del centro,
. Cada vértice está a la misma distancia del centro,  unidades.
unidades.
3 Focos: Los focos está dados por los puntos 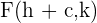 y
y 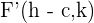 . Cada foco está a la misma distancia del centro,
. Cada foco está a la misma distancia del centro,  unidades.
unidades.
4 Eje real: Es el segmento de recta que une los vértices, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje es paralelo al eje de las abscisas.
. Este eje es paralelo al eje de las abscisas.
5 Eje imaginario: Es el segmento de recta que une los puntos  y
y  , esto es
, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje es paralelo al eje de las ordenadas.
. Este eje es paralelo al eje de las ordenadas.
6 Eje focal: Eje imaginario: Es el segmento de recta que une los focos, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  .
.
7 Las constantes  ,
,  y
y  , que definen completamente la hipérbola, satisfacen que
, que definen completamente la hipérbola, satisfacen que
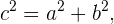
8 La excentricidad de la hipérbola está dada por
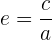
Cada punto,  , sobre la hipérbola debe cumplir que
, sobre la hipérbola debe cumplir que
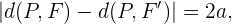
por la definición de distancia euclideana entre dos puntos, tenemos que esto es igual a
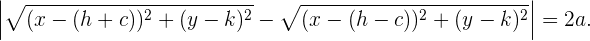
Realizando ciertas operaciones algebraicas podemos escribir la igualdad anterior de la siguiente manera
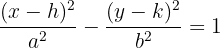
esta última ecuación se conoce como la ecuación reducida de la hipérbola con eje horizontal y con centro distinto al origen.
Ejercicios
A continuación veremos algunos ejercicios para poner en práctica nuestro entendimiendo de la ecuación
Hallar la ecuación de la hipérbola de foco  , de vértice
, de vértice  y de centro
y de centro 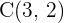
Primero, como el centro es el origen 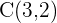 y un foco es
y un foco es  tenemos que
tenemos que

además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es 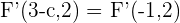 .
.
Siguiendo la misma analogía que con el foco, sabemos un vértice es  , por lo tanto
, por lo tanto
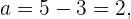
como ambos vértices están a  unidades del centro, el otro vértice es
unidades del centro, el otro vértice es  .
.
Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
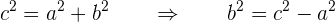
esto es
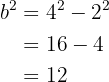
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es


Hallar la ecuación de la hipérbola con centro en 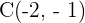 , con distancia focal igual a
, con distancia focal igual a  y eje real horizontal con valor de
y eje real horizontal con valor de 
Primero, como el centro es 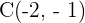 y el eje real es horizontal e igual a
y el eje real es horizontal e igual a  , de aquí podemos despejar nuestro valor de
, de aquí podemos despejar nuestro valor de  ,
,
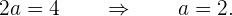
Por lo tanto nuestros vértices son

y
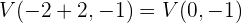
Siguiendo la misma analogía, tenemos que el eje focal también es horizontal (siempre tiene la misma derección que el eje real ya que el eje real está dentro del eje focal), ademàs de tener un valor de  , usaremos esto para obtener
, usaremos esto para obtener 

Por lo tanto nuestros focos son
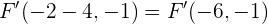
y
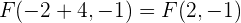
Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
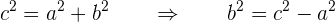
esto es
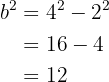
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
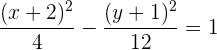
Hallar la ecuación de la hipérbola con centro en 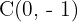 , con distancia focal igual a
, con distancia focal igual a  y eje imaginario vertical con valor de
y eje imaginario vertical con valor de 
Primero, como el centro es 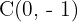 y el eje imaginario es vertical e igual a
y el eje imaginario es vertical e igual a  , de aquí podemos despejar nuestro valor de
, de aquí podemos despejar nuestro valor de  ,
,
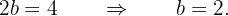
Siguiendo la misma analogía, tenemos que el eje focal también es horizontal (siempre tiene la misma derección que el eje real ya que el eje real está dentro del eje focal), ademàs de tener un valor de  , usaremos esto para obtener
, usaremos esto para obtener 
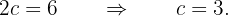
Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
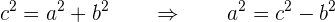
esto es
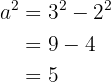
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
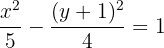
Hallar la ecuación de la hipérbola que tiene como focos los puntos 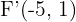 y
y 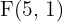 , y un eje real con valor de
, y un eje real con valor de 
Ya tenemos los focos 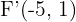 y
y 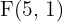 , de aquí se sigue que
, de aquí se sigue que  . Además, notemos también que el centro es
. Además, notemos también que el centro es 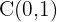 .
.
El eje real es igual a  , usaremos esto y despejaremos el valor de
, usaremos esto y despejaremos el valor de 
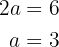
Ahora, usaremos la propiedad  para obtener a el valor de
para obtener a el valor de  . Notemos que
. Notemos que
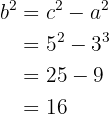
de donde se sigue inmediatamente que  . Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
. Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
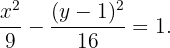
Hallar la ecuación de la hipérbola con centro 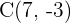 , eje focal horizontal con valor de
, eje focal horizontal con valor de  y eje imaginario vertical con valor de
y eje imaginario vertical con valor de 
Tenemos que el eje focal tiene un valor de  , de aquí obtendremos el valor de
, de aquí obtendremos el valor de 

Ahora, tenemos que el eje imaginario tiene un valor de  , por lo tanto
, por lo tanto

de aquí podemos obtener  ya que
ya que
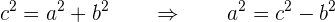
esto es
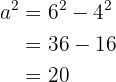
entonces 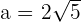 . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
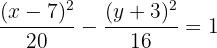
Ecuación reducida de la hipérbola no centrada en el orige con eje real vertical
En este caso el centro de la hipérbola no es el origen y su eje real es vertical, paralelo al eje de las ordenadas.
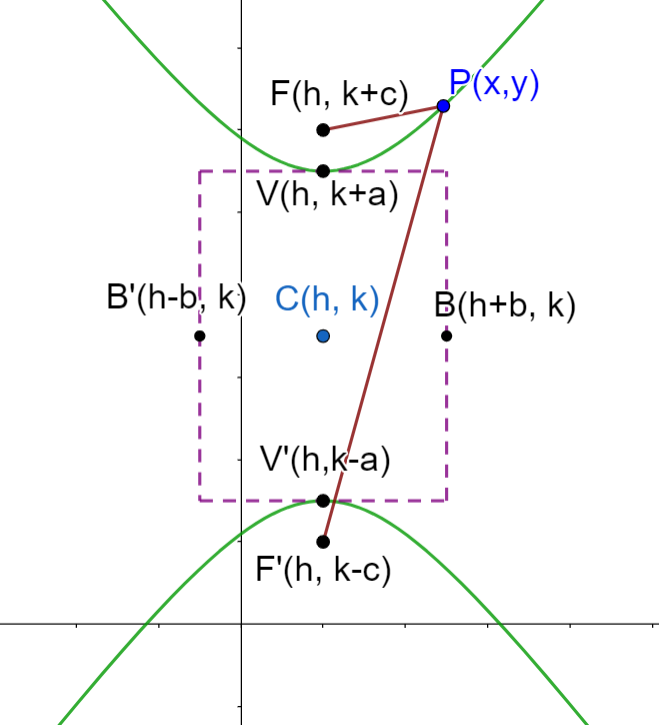
Analicemos las partes de la hipérbola que se muestran en la imagen y algunas propiedades:
1 El centro es el origen  . El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
. El centro siempre será el punto medio entre los vértices, el cual, a su vez, coincide con el punto medio de los focos.
2 Vértices: Los vértices están dados por los puntos 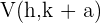 y
y 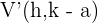 . Cada vértice está a la misma distancia del centro,
. Cada vértice está a la misma distancia del centro,  unidades.
unidades.
3 Focos: Los focos está dados por los puntos 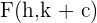 y
y 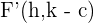 . Cada foco está a la misma distancia del centro,
. Cada foco está a la misma distancia del centro,  unidades.
unidades.
4 Eje real: Es el segmento de recta que une los vértices, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje es paralelo al eje de las ordenadas.
. Este eje es paralelo al eje de las ordenadas.
5 Eje imaginario: Es el segmento de recta que une los puntos  y
y  , esto es
, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  . Este eje es paralelo al eje de las abscisas.
. Este eje es paralelo al eje de las abscisas.
6 Eje focal: Eje imaginario: Es el segmento de recta que une los focos, esto es  , su valor (longitud) es igual a
, su valor (longitud) es igual a  .
.
7 Las constantes  ,
,  y
y  , que definen completamente la hipérbola, satisfacen que
, que definen completamente la hipérbola, satisfacen que
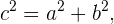
8 La excentricidad de la hipérbola está dada por
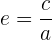
Cada punto,  , sobre la hipérbola debe cumplir que
, sobre la hipérbola debe cumplir que
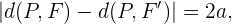
por la definición de distancia euclideana entre dos puntos, tenemos que esto es igual a
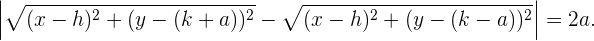
Realizando ciertas operaciones algebraicas podemos escribir la igualdad anterior de la siguiente manera
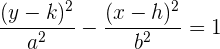
esta última ecuación se conoce como la ecuación reducida de la hipérbola con eje vertical y con centro distinto al origen.
Ejercicios
A continuación veremos algunos ejercicios para poner en práctica nuestro entendimiendo de la ecuación
Hallar la ecuación de la hipérbola de foco 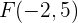 , de vértice
, de vértice  y de centro
y de centro 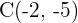
Primero, como el centro es el origen  y un foco es
y un foco es  tenemos que
tenemos que
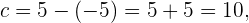
además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es 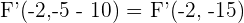 .
.
Siguiendo la misma analogía que con el foco, sabemos un vértice es  , por lo tanto
, por lo tanto
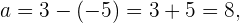
como ambos vértices están a  unidades del centro, el otro vértice es
unidades del centro, el otro vértice es  .
.
Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
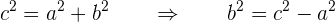
esto es
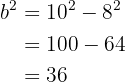
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
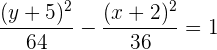

Hallar la ecuación de la hipérbola con centro 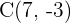 , eje focal vertical con valor de
, eje focal vertical con valor de  y eje imaginario horizontal con valor de
y eje imaginario horizontal con valor de 
Tenemos que el eje focal tiene un valor de  , de aquí obtendremos el valor de
, de aquí obtendremos el valor de 

por lo tanto los focos son 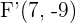 y
y 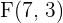 .
.
Ahora, tenemos que el eje imaginario tiene un valor de  , por lo tanto
, por lo tanto

de aquí podemos obtener  ya que
ya que
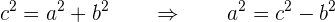
esto es
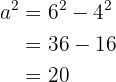
entonces 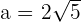 . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es

Hallar la ecuación de la hipérbola con centro en 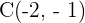 , con distancia focal igual a
, con distancia focal igual a  y eje real vertical con valor de
y eje real vertical con valor de 
Primero, como el centro es 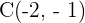 y el eje real es vertical e igual a
y el eje real es vertical e igual a  , de aquí podemos despejar nuestro valor de
, de aquí podemos despejar nuestro valor de  ,
,
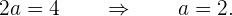
Siguiendo la misma analogía, tenemos que el eje focal también es vertical (siempre tiene la misma dirección que el eje real ya que el eje real está dentro del eje focal), ademàs de tener un valor de  , usaremos esto para obtener
, usaremos esto para obtener 

Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
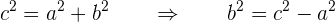
esto es
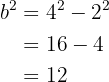
entonces  . Ya tenemos el valor de
. Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
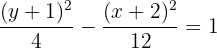
Hallar la ecuación de la hipérbola con centro 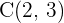 , foco
, foco 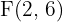 y eje imaginario igual a
y eje imaginario igual a 
Primero, como el centro es el origen 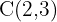 y un foco es
y un foco es 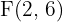 tenemos que
tenemos que  , además, sabemos que ambos focos están a
, además, sabemos que ambos focos están a  unidades del centro, por lo tanto, el otro foco es
unidades del centro, por lo tanto, el otro foco es 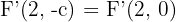 .
.
Ahora, notemos que el eje real está sobre la recta que une los focos. Esto implica que el eje real es vertical, por lo tanto el eje imaginario es horizontal. Además, tenemos que el eje imaginario tiene un valor de  , esto es
, esto es

Ahora encontremos el valor de  . Tenemos que se cumple que
. Tenemos que se cumple que
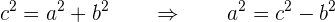
esto es
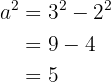
entonces  .
.
Ya tenemos el valor de  y
y  necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
necesarios para obtener nuestra ecuación reducida de la hipérbola, la cual es
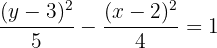
Hallar la ecuación de la hipérbola que tiene como focos los puntos 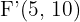 y
y 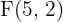 , y un eje real con valor de
, y un eje real con valor de 
Ya tenemos los focos 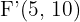 y
y 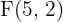 , de aquí se sigue que
, de aquí se sigue que  . Además, notemos también que el centro es
. Además, notemos también que el centro es 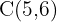 .
.
El eje real es igual a  , usaremos esto y despejaremos el valor de
, usaremos esto y despejaremos el valor de 
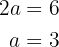
Ahora, usaremos la propiedad  para obtener a el valor de
para obtener a el valor de  . Notemos que
. Notemos que
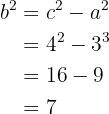
de donde se sigue inmediatamente que 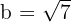 . Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
. Ya tenemos lo necesario para obtener la ecuaciòn reducida de nuestra hipérbola, la cual es
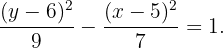
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5