Capítulos
En el plano cartesiano, la parábola corresponde al lugar geométrico formado por los puntos 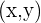 que equidistan de un punto fijo llamado foco y una recta dada llamada directriz. Así, dado un foco
que equidistan de un punto fijo llamado foco y una recta dada llamada directriz. Así, dado un foco  y una directriz
y una directriz  , los puntos
, los puntos  pertenecen a la parábola si satisfacen que:
pertenecen a la parábola si satisfacen que:
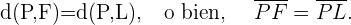
La distancia de  a
a  se conoce como distancia focal
se conoce como distancia focal  ; ésta se obtiene trazando una perpendicular a
; ésta se obtiene trazando una perpendicular a  que pase por
que pase por  , después se calcula la longitud del segmento comprendido entre la directriz y el foco. El punto que destaca de la parábola se llama vértice
, después se calcula la longitud del segmento comprendido entre la directriz y el foco. El punto que destaca de la parábola se llama vértice 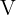 , pues su distancia tanto al foco como a la directriz es de
, pues su distancia tanto al foco como a la directriz es de  . Geométricamente, corresponde al punto punto medio del segmento trazado para calcular la distancia focal.
. Geométricamente, corresponde al punto punto medio del segmento trazado para calcular la distancia focal.

Ecuación ordinaria reducida de la parábola de eje horizontal
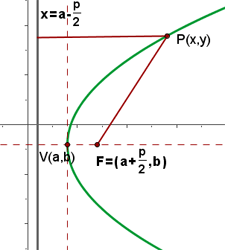
Supongamos que la directriz es una recta vertical paralela al eje de las ordenadas, que se encuentra al lado izquierdo de ésta. Si el vértice tiene como coordenadas 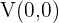 , entonces, las coordenadas del foco deben ser
, entonces, las coordenadas del foco deben ser 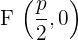 y la recta directriz
y la recta directriz 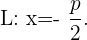

Los puntos  pertenecen a la parábola si están a la misma distancia del foco que de la directriz, así:
pertenecen a la parábola si están a la misma distancia del foco que de la directriz, así:
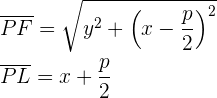

Simplificando la expresión, se obtiene la ecuación reducida de la parábola cuando ésta abre a la derecha:
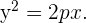
En caso de que la recta se encuentre del lado derecho del eje de las ordenadas y el vértice tenga como coordenadas 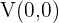 , las coordenadas del foco deben ser
, las coordenadas del foco deben ser 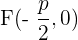 y la recta directriz
y la recta directriz 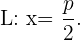
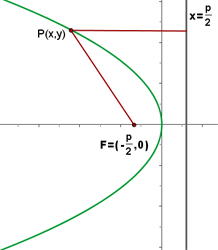
Haciendo el mismo procedimiento descrito anteriormente, se obtiene la ecuación reducida de la parábola cuando ésta abre a la izquierda:
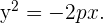
Ejemplos
1 Dada la parábola 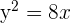 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.


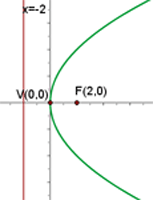
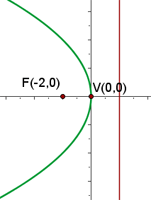
2 Dada la parábola 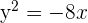 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.

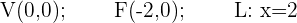
Ecuación ordinaria reducida de la parábola de eje vertical
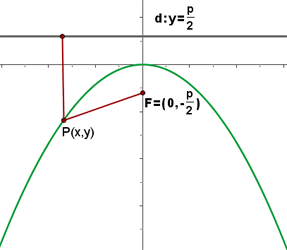
Supongamos que la directiz es una recta horizontal paralela al eje de las abscisas, que se encuentra debajo de ésta. Si el vértice tiene como coordenadas 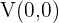 , entonces, las coordenadas del foco deben ser
, entonces, las coordenadas del foco deben ser 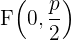 y la recta directriz
y la recta directriz 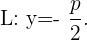

Los puntos  pertenecen a la parábola si están a la misma distancia del foco que de la directriz, así:
pertenecen a la parábola si están a la misma distancia del foco que de la directriz, así:
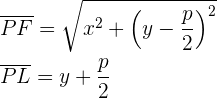
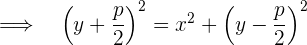
Simplificando la expresión, se obtiene la ecuación reducida de la parábola cuando ésta abre a la derecha:

En caso de que la recta se encuentre arriba del eje de las abscisas y el vértice tenga como coordenadas 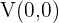 , las coordenadas del foco deben ser
, las coordenadas del foco deben ser 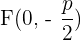 y la recta directriz
y la recta directriz 
Haciendo el mismo procedimiento descrito anteriormente, se obtiene la ecuación reducida de la parábola cuando ésta abre a la izquierda:
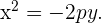
Ejemplos
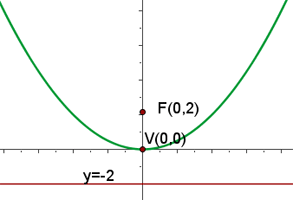
1 Dada la parábola 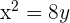 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.


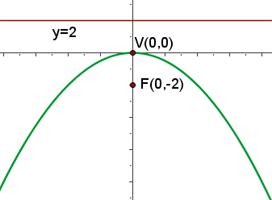
2 Dada la parábola 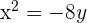 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.

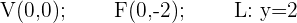
Ecuaciones ordinarias de la parábola
En caso de que el vértice tenga coordenadas  distintas de cero, las ecuaciones que se obtienen son muy parecidas a las explicadas anteriormente salvo una traslación.
distintas de cero, las ecuaciones que se obtienen son muy parecidas a las explicadas anteriormente salvo una traslación.
Si la recta directriz es paralela al eje de las ordenadas:.

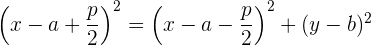
Simplificando la expresión, se obtiene la ecuación ordinaria de la parábola cuando abre a la derecha:

Si el valor de  es negativo, indica que abre a la izquierda.
es negativo, indica que abre a la izquierda.
En el caso de que la recta directriz sea paralela al eje de las abscisas.

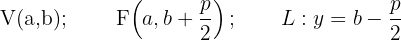
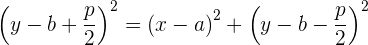
Simplificando la expresión, se obtiene la ecuación ordinaria de la parábola cuando ésta abre hacia arriba:

Si el valor de  es negativo, indica que abre hacia abajo.
es negativo, indica que abre hacia abajo.
Ejemplos
1 Dada la parábola 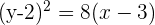 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.

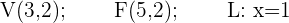
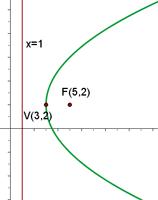
2Dada la parábola 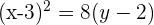 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.

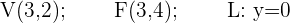

Ejercicios resueltos sobre parábolas
Con los datos dados, determina las ecuaciones de las parábolas
De directriz  , de foco
, de foco 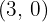 .
.

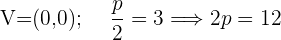
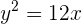
De directriz  , de vértice
, de vértice  .
.
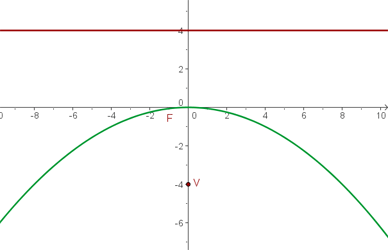
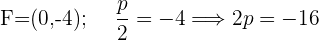
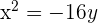
De directriz 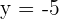 , de foco
, de foco  .
.
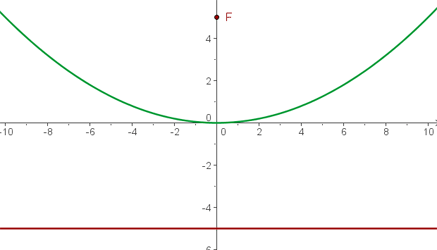
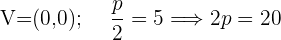
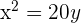
De directriz  , de foco
, de foco 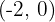 .
.
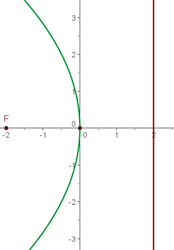
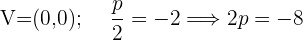
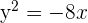
De foco  , de vértice
, de vértice  .
.

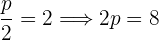
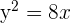
De foco 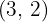 , de vértice
, de vértice 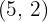 .
.


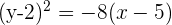
De foco 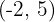 , de vértice
, de vértice  .
.
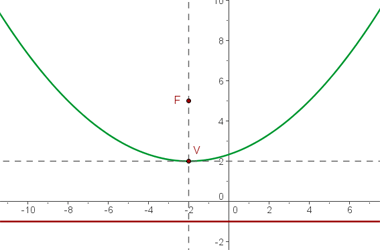
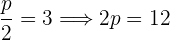

De foco  , de vértice
, de vértice 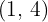 .
.

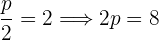

Con las ecuaciones de las parábolas dadas, calcula las coordenadas del vértice y del foco, así como las ecuaciones de las directrices


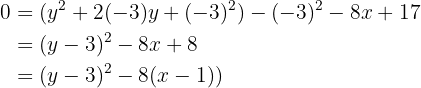
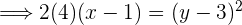
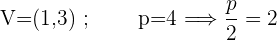


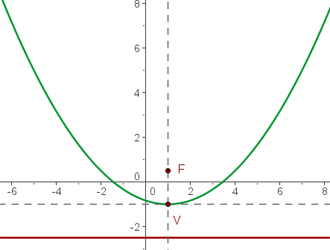
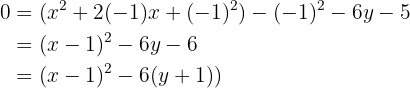
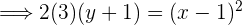
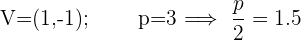



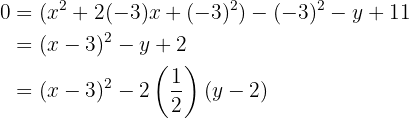


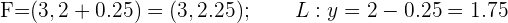
Resuelve los problemas
Determina la ecuación de la parábola que tiene por directriz la recta  y por foco el punto
y por foco el punto  .
.
La ecuación ordinaria que se utilizará es 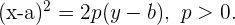
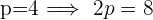

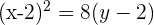
Escribe la ecuación de la parábola de eje vertical cuyo vértice se encuentra en el eje de las abscisas, la cual pasa por los puntos 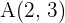 y
y 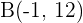 .
.
La ecuación ordinaria que se utilizará es 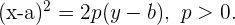 Además, su vértice es de la forma
Además, su vértice es de la forma  .
.
Se forma un sistema de dos ecuaciones con dos incógnitas, sustituyendo los puntos conocidos de la parábola y el valor del vértice.
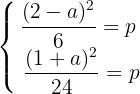
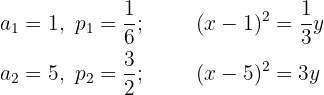
Si quieres encontrar tu profesor matematicas ideal, Superprof es tu sitio.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5