¡Bienvenidos a nuestra página dedicada a problemas y ejercicios resueltos de la ecuación de la hipérbola! Aquí, exploraremos las características de esta curva fascinante que se encuentra en el corazón de la geometría analítica. Aquí, desglosaremos problemas de la ecuación de la hiperbola paso a paso, para que puedas comprender y dominar esta forma geométrica en profundidad.
Además, te guiaremos a través de ejemplos prácticos y ejercicios resueltos que te ayudarán a desarrollar una sólida comprensión de la hiperbola. Ya sea que estés estudiando para un examen o simplemente tengas curiosidad por explorar las maravillas de las curvas hiperbólicas, ¡esta página es tu recurso definitivo! Así que prepárate para sumergirte en el intrigante mundo de las ecuaciones de la hiperbola.
Hallar la ecuación de la hipérbola de foco  , de vértice
, de vértice  y de centro
y de centro 
1Como el centro y el vértice se encuentran sobre el eje horizontal, entonces la ecuación es de la forma

Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus vértices
, el cual es igual a la distancia del centro a uno de sus vértices

2Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus focos
, el cual es igual a la distancia del centro a uno de sus focos

3Calculamos el valor de 

3La ecuación de la hipérbola es

Hallar la ecuación de la hipérbola de foco  , de vértice
, de vértice  y de centro
y de centro 
1Como el centro y el vértice se encuentran sobre el eje vertical, entonces la ecuación es de la forma

Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus vértices
, el cual es igual a la distancia del centro a uno de sus vértices

2Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus focos
, el cual es igual a la distancia del centro a uno de sus focos

3Calculamos el valor de 

3La ecuación de la hipérbola es

Hallar la ecuación de la hipérbola de foco  , de vértice
, de vértice  y de centro
y de centro 
1Como el centro y el vértice se tienen la misma coordenada  , entonces la ecuación es de la forma
, entonces la ecuación es de la forma
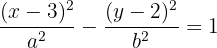
Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus vértices
, el cual es igual a la distancia del centro a uno de sus vértices
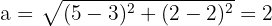
2Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus focos
, el cual es igual a la distancia del centro a uno de sus focos
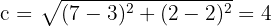
3Calculamos el valor de 

4La ecuación de la hipérbola es
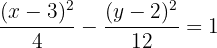
Hallar la ecuación de la hipérbola de foco  , de vértice
, de vértice  y de centro
y de centro 
1Como el centro y el vértice se tienen la misma coordenada  , entonces la ecuación es de la forma
, entonces la ecuación es de la forma
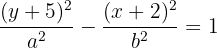
Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus vértices
, el cual es igual a la distancia del centro a uno de sus vértices
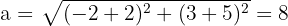
2Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus focos
, el cual es igual a la distancia del centro a uno de sus focos
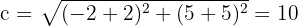
3Calculamos el valor de 

4La ecuación de la hipérbola es
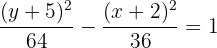
Hallar la ecuación y la excentricidad de la hipérbola que tiene como focos los puntos 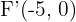 y
y  y
y  como diferencia de los radios vectores.
como diferencia de los radios vectores.
1Como los se encuentran sobre el eje horizontal y son simétricos respecto al origen, entonces el centro es  y la ecuación es de la forma
y la ecuación es de la forma

Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus focos
, el cual es igual a la distancia del centro a uno de sus focos
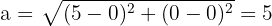
2Como la diferencia de los radio vectores es  , entonces
, entonces  , luego
, luego 
3Calculamos el valor de 

4La ecuación de la hipérbola es
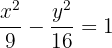
5La excentricidad es

Hallar la ecuación y la excentricidad de la hipérbola que tiene como focos los puntos 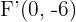 y
y 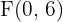 y
y  como diferencia de los radios vectores
como diferencia de los radios vectores
1Como los focos se encuentran sobre el eje vertical y son simétricos respecto al origen, entonces el centro es  y la ecuación es de la forma
y la ecuación es de la forma

Calculamos el valor de  , el cual es igual a la distancia del centro a uno de sus focos
, el cual es igual a la distancia del centro a uno de sus focos

2Como la diferencia de los radio vectores es  , entonces
, entonces 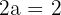 , luego
, luego 
3Calculamos el valor de 

4La ecuación de la hipérbola es
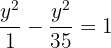
5La excentricidad es

Hallar las coordenadas de los vértices y de los focos, las ecuaciones de las asíntotas y la excentricidad de la hipérbola 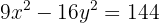
1Primero escribimos la ecuación de la hipérbola en su forma reducida, para ello se divide ambos lados por 
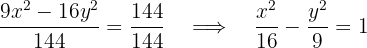
entonces  y
y 
2Calculamos el valor de 
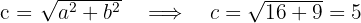
3Las coordenadas de los vértices son
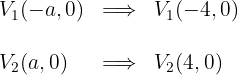
4Las coordenadas de los focos son
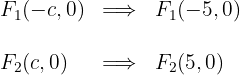
5Las ecuaciones de las asíntotas son
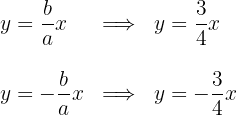
6La excentricidad es
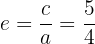
Hallar las coordenadas de los vértices y de los focos, las ecuaciones de las asíntotas y la excentricidad de la hipérbola 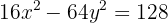
1Primero escribimos la ecuación de la hipérbola en su forma reducida, para ello se divide ambos lados por 
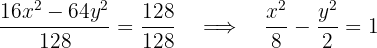
entonces  y
y 
2Calculamos el valor de 

3Las coordenadas de los vértices son

4Las coordenadas de los focos son

5Las ecuaciones de las asíntotas son
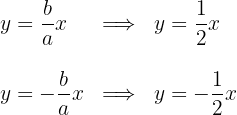
6La excentricidad es
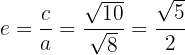
Representa gráficamente y determina las coordenadas de los focos, de los vértices y la excentricidad de las siguientes hipérbolas:
9.1
9.2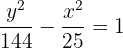
1.1Para la primera hipérbola de la ecuación se tienen los valores de 
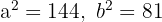 y
y 
1.2Calculamos el valor de 

1.3El eje real es horizontal y la hipérbola tiene centro en el origen, por lo que las coordenadas de los vértices son
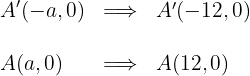
1.4Las coordenadas de los focos son
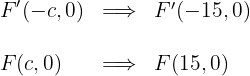
1.5La excentricidad es

1.6La gráfica es

2.1Para la segunda hipérbola de la ecuación se tienen los valores de 
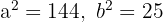 y
y 
2.2Calculamos el valor de 

2.3El eje real es vertical y la hipérbola tiene centro en el origen, por lo que las coordenadas de los vértices son
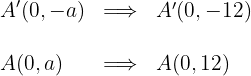
2.4Las coordenadas de los focos son
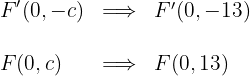
2.5La excentricidad es

2.6La gráfica es

Representa gráficamente y determina las coordenadas de los focos, de los vértices y la excentricidad de las siguientes hipérbolas:
10.1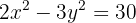
10.2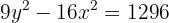
1.1Para la primera hipérbola expresamos su ecuación en la forma reducida dividiendo ambos lados por 
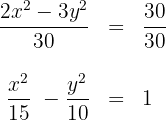
de la ecuación se obtienen los valores de  y el centro
y el centro
 y
y 
1.2Calculamos el valor de 
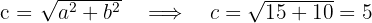
1.3El eje real es horizontal y la hipérbola tiene centro en el origen, por lo que las coordenadas de los vértices son
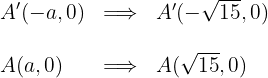
1.4Las coordenadas de los focos son
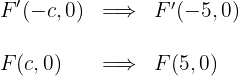
1.5La excentricidad es
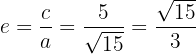
1.6La gráfica es

2.1Para la segunda hipérbola expresamos su ecuación en la forma reducida dividiendo ambos lados por 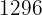
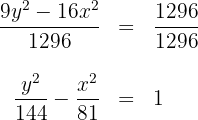
de la ecuación se obtienen los valores de  y el centro
y el centro
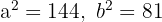 y
y 
2.2Calculamos el valor de 

2.3El eje real es vertical y la hipérbola tiene centro en el origen, por lo que las coordenadas de los vértices son
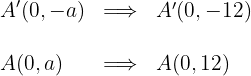
2.4Las coordenadas de los focos son
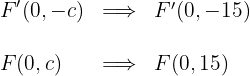
2.5La excentricidad es

2.6La gráfica es

Representa gráficamente y determina las coordenadas de los focos, de los vértices y la excentricidad de las siguientes hipérbolas:
11.1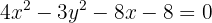
11.2
1.1Para la primera hipérbola expresamos su ecuación en la forma reducida
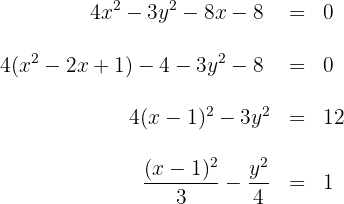
de la ecuación se obtienen los valores de  y el centro
y el centro
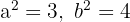 y
y 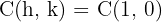
1.2Calculamos el valor de 
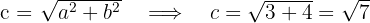
1.3El eje real es horizontal y la hipérbola tiene centro 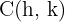 , por lo que las coordenadas de los vértices son
, por lo que las coordenadas de los vértices son
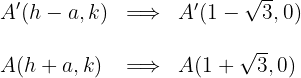
1.4Las coordenadas de los focos son

1.5La excentricidad es
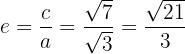
1.6La gráfica es

2.1Para la segunda hipérbola expresamos su ecuación en la forma reducida

de la ecuación se obtienen los valores de  y el centro
y el centro
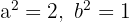 y
y 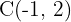
2.2Calculamos el valor de 
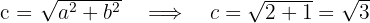
2.3El eje real es vertical y la hipérbola tiene centro en 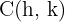 , por lo que las coordenadas de los vértices son
, por lo que las coordenadas de los vértices son

2.4Las coordenadas de los focos son

2.5La excentricidad es
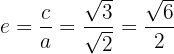
2.6La gráfica es

Hallar la ecuación de una hipérbola de eje real horizontal  y distancia focal
y distancia focal 
1Como el eje real es igual a 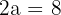 , entonces
, entonces 
2Como la distancia focal es igual a  , entonces
, entonces 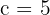
3Calculamos el valor de 
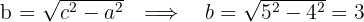
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es

Hallar la ecuación de una hipérbola de eje imaginario vertical  y distancia focal
y distancia focal 
1Como el eje imaginario es igual a 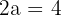 , entonces
, entonces 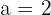
2Como la distancia focal es igual a  , entonces
, entonces 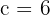
3Calculamos el valor de 
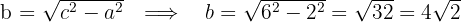
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es

El eje real de una hipérbola mide  , es horizontal, con centro en el origen y pasa por el punto
, es horizontal, con centro en el origen y pasa por el punto  . Hallar su ecuación
. Hallar su ecuación
1Como el eje real es igual a  , entonces
, entonces 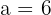
2La ecuación de la hipérbola es

3Como la hipérbola pasa por el punto  sustituimos y calculamos el valor de
sustituimos y calculamos el valor de 

4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es
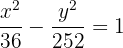
Calcular la ecuación reducida de la hipérbola con centro en el origen, eje real horizontal, distancia focal 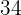 y la distancia de un foco al vértice más próximo es
y la distancia de un foco al vértice más próximo es 
1Como la distancia focal es igual a  , entonces
, entonces 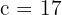
2Como la distancia de un foco a un vértice más próximo es 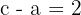 , entonces
, entonces 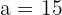
3Calculamos 
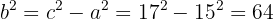
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es
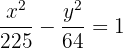
El eje principal de una hipérbola es horizontal y mide  , la excentricidad es
, la excentricidad es  . Calcular la ecuación de la hipérbola
. Calcular la ecuación de la hipérbola
1Como el eje principal es  , entonces
, entonces 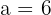
2Como la excentricidad es 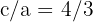 , entonces
, entonces 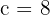
3Calculamos 
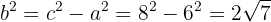
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es
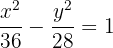
Calcular la ecuación de una hipérbola equilátera sabiendo que su distancia focal es 
1Como la distancia focal es  , entonces
, entonces 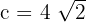
2Como la hipérbola es equilátera, entonces  , luego
, luego

3Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es

El eje imaginario de una hipérbola es vertical, mide  y las ecuaciones de las asíntotas son
y las ecuaciones de las asíntotas son 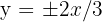 . Calcular la ecuación de la hipérbola, sus ejes, focos y vértices
. Calcular la ecuación de la hipérbola, sus ejes, focos y vértices
1Como el eje imaginario es  , entonces
, entonces 
2Como la pendiente de las asíntotas es 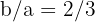 , entonces
, entonces 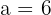
3Calculamos 

4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es
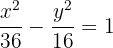
5Las coordenadas de los vértices son
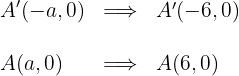
6Las coordenadas de los focos son
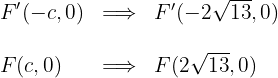
Determina la ecuación reducida de una hipérbola con eje real horizontal, centro en el origen y que pasa por los puntos 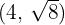 y
y 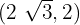
1La ecuación de la hipérbola es de la forma

2Como la hipérbola pasa por los puntos 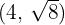 y
y 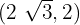 , entonces al sustituir se obtiene un sistema de ecuaciones en términos de
, entonces al sustituir se obtiene un sistema de ecuaciones en términos de 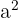 y
y 
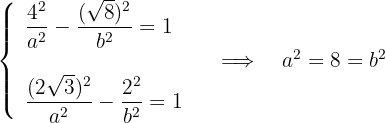
3La ecuación de la hipérbola es
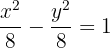
Determina la ecuación reducida de una hipérbola con eje real horizontal, centro en el origen, pasa por el punto  y su excentricidad es
y su excentricidad es 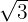
1La ecuación de la hipérbola es de la forma

2Como la hipérbola pasa por el punto  , entonces al sustituir se obtiene
, entonces al sustituir se obtiene
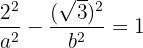
3Como la excentricidad 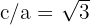 y
y 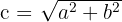 , entonces al sustituir se obtiene
, entonces al sustituir se obtiene

4Se tiene el siguiente sistema de ecuaciones, del cual se obtiene
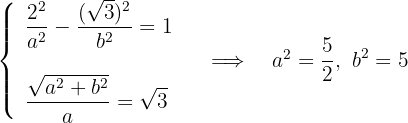
5La ecuación de la hipérbola es

Determina la ecuación reducida de una hipérbola con centro en el origen, eje real horizontal y sabiendo que un foco dista de los vértices de la hipérbola  y
y 
1De los datos anteriores se tiene que el eje real es igual a 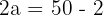 , entonces
, entonces 
2Como la distancia focal es igual a 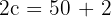 , entonces
, entonces 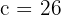
3Calculamos el valor de 
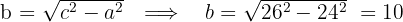
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es

Determina la posición relativa de la recta 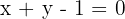 con respecto a la hipérbola
con respecto a la hipérbola 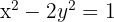
1Determinamos los puntos de intersección de ambas curvas, para ello despejamos la variable  en la recta,
en la recta, 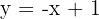 y sustituimos en la hipérbola
y sustituimos en la hipérbola

Así, las raíces son  y
y 
2sustituyendo los valores de  en la ecuación de la recta, obtenemos lo puntos de intersección
en la ecuación de la recta, obtenemos lo puntos de intersección 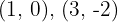
3La gráfica viene dada por

Una hipérbola equilátera pasa por el punto 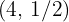 . Hallar su ecuación referida a sus asíntotas como ejes, y las coordenadas de los vértices
. Hallar su ecuación referida a sus asíntotas como ejes, y las coordenadas de los vértices
1Determinamos la ecuación de la hipérbola, para ello multiplicamos 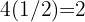 . Así, la ecuación de la hipérbola equilátera es
. Así, la ecuación de la hipérbola equilátera es 
2Al ser la hipérbola equilátera, 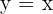 es la recta que contiene al eje real. Los vértices se obtienen de resolver el sistema de ecuaciones
es la recta que contiene al eje real. Los vértices se obtienen de resolver el sistema de ecuaciones

3La gráfica viene dada por

Halla la ecuación de una hipérbola equilátera sabiendo que  . ¿Qué coordenadas tienen los focos?
. ¿Qué coordenadas tienen los focos?
1Como la hipérbola es equilátera, entonces  , luego
, luego
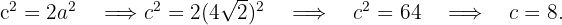
2Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es 
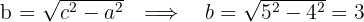
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es

Las coordenadas de los focos son: 
El eje principal de una hipérbola es horizontal y mide  , la excentricidad es
, la excentricidad es  . Calcular la ecuación de la hipérbola
. Calcular la ecuación de la hipérbola
1Como el eje principal es 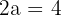 , entonces
, entonces 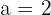
2Como la excentricidad es 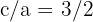 , entonces
, entonces 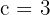
3Calculamos 
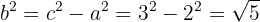
4Consideramos el centro en el origen, por lo que la ecuación de la hipérbola es
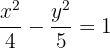
Si buscas profesores particulares matematicas Madrid, Superprof es tu sitio.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5