La parábola es una colección infinita de puntos que se encuentran a la misma distancia de una recta fija y un punto fijo en el plano. La definición anterior también es conocida como el lugar geométrico de la parábola.
La parábola contiene elementos característicos como la directriz y el foco, que son la recta y el punto, ambos fijos mencionados en la definición. También posee un vértice el cual es el punto más cercano a la directriz y el foco.
En los siguientes problemas y ejercicios trabajamos dos modalidades: obtenemos los elementos de la parábola a partir de conocer su ecuación, y si conocemos los elementos de la parábola obtenemos su ecuación.

Obtener los elementos de la parábola
Dada la parábola 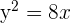 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.
El parámetro es

Se trata de una ecuación reducida por lo que el vértice está en el origen
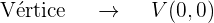
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OX. Además, la parábola se encuentra en el lado positivo del eje OX, ya que el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OX. Además, la parábola se encuentra en el lado positivo del eje OX, ya que el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 8 que es positivo, por lo que
) es 8 que es positivo, por lo que
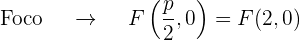
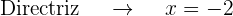
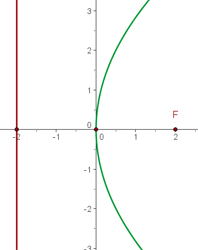
La gráfica de la parábola 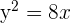 es
es
Dada la parábola 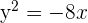 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.
El parámetro es

Se trata de una ecuación reducida por lo que el vértice está en el origen
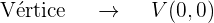
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OX. Además, la parábola se encuentra en el lado negativo del eje OX, ya que el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OX. Además, la parábola se encuentra en el lado negativo del eje OX, ya que el coeficiente que acompaña al término no cuadrático (en este caso la  ) es -8 que es negativo, por lo que
) es -8 que es negativo, por lo que
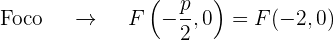
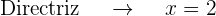
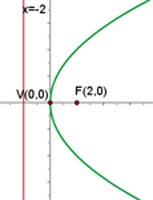
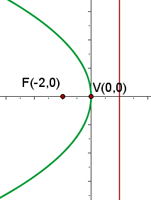
La gráfica de la parábola 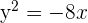 es
es
Dada la parábola 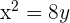 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.
El parámetro es

Se trata de una ecuación reducida por lo que el vértice está en el origen
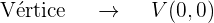
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OY. Además, la parábola se encuentra en el lado positivo del eje OY, ya que el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OY. Además, la parábola se encuentra en el lado positivo del eje OY, ya que el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 8 que es positivo, por lo que
) es 8 que es positivo, por lo que
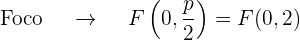
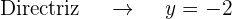
La gráfica de la parábola 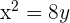 es
es

Dada la parábola 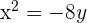 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.
El parámetro es

Se trata de una ecuación reducida por lo que el vértice está en el origen
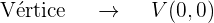
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OY. Además, la parábola se encuentra en el lado negativo del eje OY, ya que el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OY. Además, la parábola se encuentra en el lado negativo del eje OY, ya que el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 8 que es negativo, por lo que
) es 8 que es negativo, por lo que
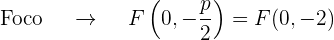
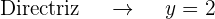
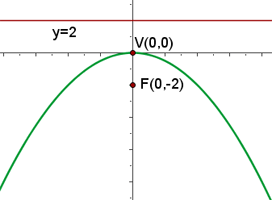
La gráfica de la parábola 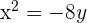 es
es
Dada la parábola 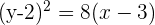 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.
El parámetro es

No se trata de una ecuación reducida, por lo que el vértice está en

El término cuadrático en la ecuación es la  así que el eje de la parábola es paralelo al eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola es paralelo al eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 8 que es positivo, por lo que el foco está al lado derecho del vértice
) es 8 que es positivo, por lo que el foco está al lado derecho del vértice
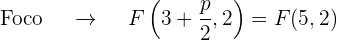
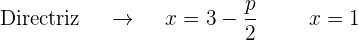
La gráfica de la parábola 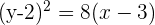 es
es
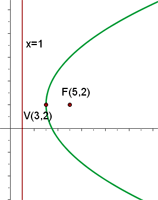
Dada la parábola 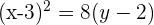 , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.
El parámetro es

No se trata de una ecuación reducida, por lo que el vértice está en

El término cuadrático en la ecuación es la  así que el eje de la parábola es paralelo al eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola es paralelo al eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 8 que es positivo, por lo que el foco está al lado derecho del vértice
) es 8 que es positivo, por lo que el foco está al lado derecho del vértice

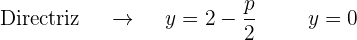
La gráfica de la parábola 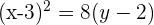 es
es

Determinar, en forma reducida, las ecuaciones de las siguientes parábolas, indicando el valor del parámetro, las coordenadas del foco y la ecuación de la directriz.
1 
Despejamos el término 


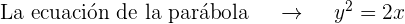
El parámetro es

Se trata de una ecuación reducida, por lo que el vértice está en el origen
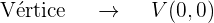
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 2 que es positivo, por lo que el foco está al lado derecho del vértice
) es 2 que es positivo, por lo que el foco está al lado derecho del vértice
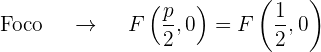
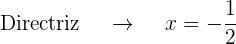
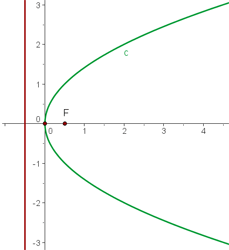
La gráfica de la parábola  es
es
2 
Despejamos el término 


El parámetro es

Se trata de una ecuación reducida, por lo que el vértice está en el origen
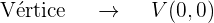
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es
) es 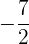 que es negativo, por lo que el foco está al lado izquierdo del vértice
que es negativo, por lo que el foco está al lado izquierdo del vértice
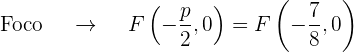
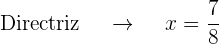
La gráfica de la parábola  es
es
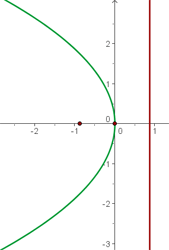
3 
Despejamos el término 


El parámetro es

Se trata de una ecuación reducida, por lo que el vértice está en el origen
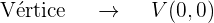
El término cuadrático en la ecuación es la  así que el eje de la parábola coincide con el eje OY. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola coincide con el eje OY. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es
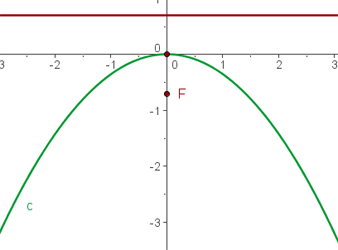
) es 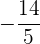 que es negativo, por lo que el foco está abajo del vértice
que es negativo, por lo que el foco está abajo del vértice
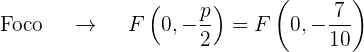
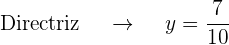
La gráfica de la parábola 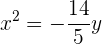 es
es
Calcular las coordenadas del vértice y de los focos, y las ecuaciones de la directrices de las parábolas:
Calcular las coordenadas del vértice y de los focos, y las ecuaciones de la directrices de las parábolas:
1 
Completamos el cuadrado

Simplificamos
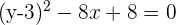
Despejamos
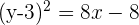

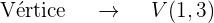
El parámetro es

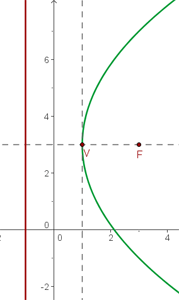
El término cuadrático en la ecuación es la  así que el eje de la parábola es paralelo al eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola es paralelo al eje OX. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 8 que es positivo, por lo que el foco está al lado derecho del vértice
) es 8 que es positivo, por lo que el foco está al lado derecho del vértice
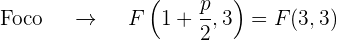
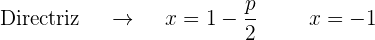
2 

Completamos el cuadrado

Simplificamos

Despejamos
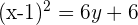

Entonces,

El parámetro es

El término cuadrático en la ecuación es la  así que el eje de la parábola es paralelo al eje OY. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola es paralelo al eje OY. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 6 que es positivo, por lo que el foco está más arriba del vértice
) es 6 que es positivo, por lo que el foco está más arriba del vértice
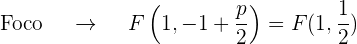
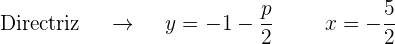
3 

Completamos el cuadrado

Simplificamos
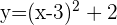
Despejamos
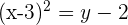

El parámetro es

El término cuadrático en la ecuación es la  así que el eje de la parábola es paralelo al eje OY. Además, el coeficiente que acompaña al término no cuadrático (en este caso la
así que el eje de la parábola es paralelo al eje OY. Además, el coeficiente que acompaña al término no cuadrático (en este caso la  ) es 1 que es positivo, por lo que el foco está más arriba del vértice
) es 1 que es positivo, por lo que el foco está más arriba del vértice
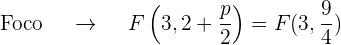

Obtener la ecuación de la parábola
Determina las ecuaciones de las parábolas que tienen:
- De directriz
 , de foco
, de foco 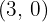 .
. - De directriz
 , de vértice
, de vértice  .
. - De directriz
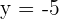 , de foco
, de foco  .
. - De directriz
 , de foco
, de foco 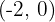 .
. - De foco
 , de vértice
, de vértice  .
. - De foco
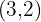 , de vértice
, de vértice 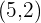 .
. - De foco
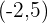 , de vértice
, de vértice 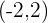 .
. - De foco
 , de vértice
, de vértice 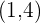 .
.
Determina las ecuaciones de las parábolas que tienen:
1 De directriz  , de foco
, de foco 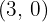 .
.
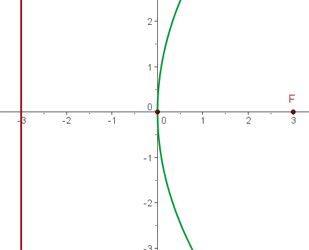
Primero calculamos la distancia entre el foco y la directriz y así obtener el parámetro  .
.

Como el foco se encuentra sobre el eje OX, la directriz es paralela al eje OY, y son equidistantes al origen, se trata de una ecuación reducida,
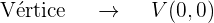
Entonces, como el eje coincide con el eje OX y el foco está más a la derecha que el vértice, la ecuación está dada por

2 De directriz  , de vértice
, de vértice  .
.
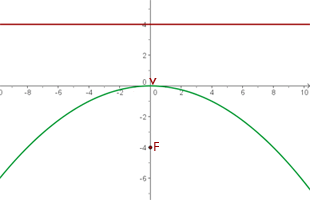
Primero calculamos la distancia entre el vértice y la directriz y así obtener 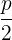 .
.

Notamos que el vértice está en el origen y la directriz es paralela al eje OX, así que se trata de una ecuación reducida.
Como el eje coincide con el eje OY y el foco está más abajo que el vértice, la ecuación será
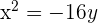
3 De directriz 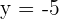 , de foco
, de foco  .
.
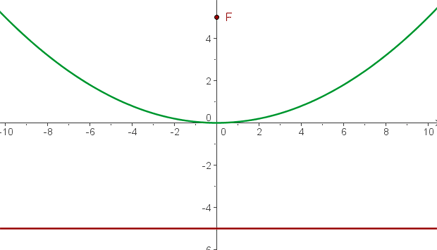
Primero calculamos la distancia entre el foco y la directriz y así obtener el parámetro  .
.
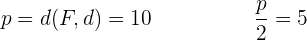
Notamos que la directriz es paralela al eje OX, y que el foco está sobre el eje OY, y son equidistantes al origen, así que se trata de una ecuación reducida.
Como el foco está más arriba que la directriz, la ecuación será
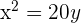
4 De directriz  , de foco
, de foco 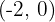 .
.
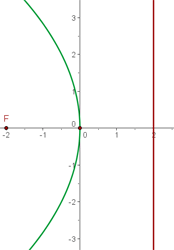
Primero calculamos la distancia entre el foco y la directriz y así obtener el parámetro  .
.
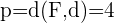
Notamos que la directriz es paralela al eje OY, y que el foco está sobre el eje OX, y son equidistantes al origen, así que se trata de una ecuación reducida.
Como el foco está más a la izquierda que la directriz, la ecuación será
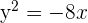
5 De foco  , de vértice
, de vértice  .
.
Primero calculamos la distancia entre el foco y el vértice y así obtener el parámetro 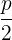 .
.
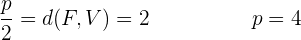
Notamos que la directriz es paralela al eje OY, y que el foco está sobre el eje OX, y son equidistantes al origen, así que se trata de una ecuación reducida.
Como el foco está más a la derecha que la directriz, la ecuación será
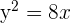
6 De foco 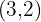 , de vértice
, de vértice 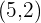 .
.
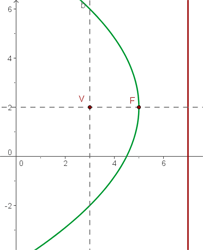
Primero calculamos la distancia entre el foco y la directriz y así obtener 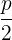 .
.
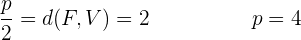
Notamos que la directriz es paralela al eje OY.
Como el foco está más a la izquierda que el vértice, la ecuación será
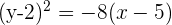
7 De foco 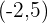 , de vértice
, de vértice 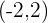 .
.
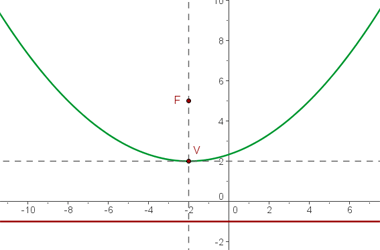
Primero calculamos la distancia entre el foco y el vértice y así obtener 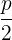 .
.
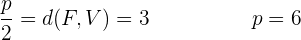
Notamos que la directriz 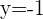 y es paralela al eje OX.
y es paralela al eje OX.
Como el foco está más arriba que el vértice, la ecuación será

8 De foco  , de vértice
, de vértice 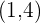 .
.
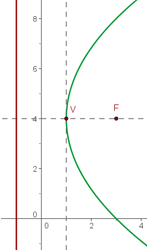
Primero calculamos la distancia entre el foco y el vértice y así obtener el parámetro  .
.
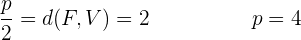
Notamos que la directriz es paralela al eje OY.
Como el foco está más a la izquiera que el vértice, la ecuación será

Hallar la ecuación de la parábola cuyo vértice coincide con el origen de coordenadas y pasa por el punto  , siendo su eje OX.
, siendo su eje OX.
Como su vértice es el origen, y su eje coincide con el eje OX del plano, su ecuación es de forma reducida, en particular es

Pasa por el punto (3,4), así que sus coordenadas cumplen la ecuación anterior, es decir,
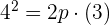
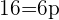
Dividimos entre 3

Así, la ecuación queda
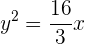
Escribe la ecuación de la parábola de eje paralelo a OY, vértice en OX y que pasa por los puntos  y
y 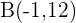 .
.
Del problema sabemos que

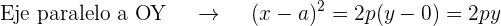
Como la curva pasa por los puntos A y B sus coordenadas deben satisfacer la ecuación de la parábola,
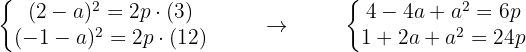
Tomamos la primera ecuación y la multiplicamos por 4, obtenemos:

Le restamos la segunda ecuación es decir, la sumamos con el negativo

Y así obtener


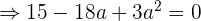
Simplificamos dividiendo todo entre 3
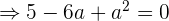
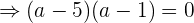
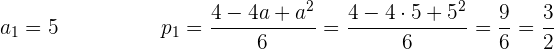

Las dos soluciones de
 me brindan dos soluciones de ecuaciones de parábolas distintas.
me brindan dos soluciones de ecuaciones de parábolas distintas.
Determina la ecuación de la parábola que tiene por directriz la recta: 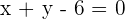 y por foco el origen de coordenadas.
y por foco el origen de coordenadas.
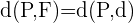

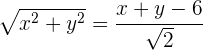
Elevamos al cuadrado para deshacernos de la raíz
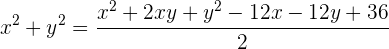
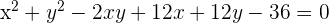
Hallar la ecuación de la parábola de eje vertical y que pasa por los puntos: 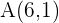 ,
, 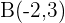 ,
,  .
.
La ecuación tiene que ser de la forma
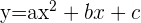
Si pasa por los puntos A, B y C, sus coordenadas cumplen la ecuación anterior
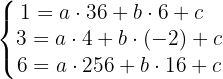
Resolviendo el sistema de 3 incógnitas obtenemos que
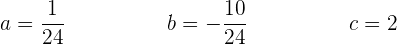
Finalmente

Determina la ecuación de la parábola que tiene por directriz la recta:  y por foco el punto
y por foco el punto  .
.
Determina la ecuación de la parábola que tiene por directriz la recta: y = 0 y por foco el punto (2, 4).
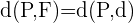
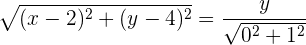
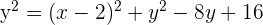
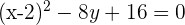
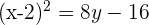
Finalmente la ecuación parabólica que obtengo es:

Calcular la posición relativa de la recta  respecto a la parábola
respecto a la parábola 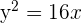 .
.
Calcular la posición relativa de la recta r ≡ x + y − 5 = 0 respecto a la parábola y² = 16 x.
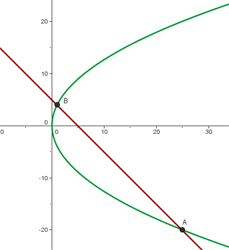

Desarrollamos


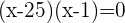
Resolvemos

No dudes en ponerte en contacto con Superprof para que te ayudemos a encontrar el curso de matematicas perfecto.
¿Buscas un profesor particular matematicas Madrid?
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar el vértice foco distancia focal la directriz la ecuación de la parábola y graficar V (-5,0) D>X=0
Calcula los elementos y las ecuaciones de la parábola como se hace eso
Hola se supone que para hacerlo te tienen que dar datos, por ejemplo si el vértice esta en el origen o no, si te dan la coordenada del foco o la ecuación directriz, si es parábola vertical u horizontal, según sea el caso, teniendo los datos necesarios solo tienes que sustituir en las fórmulas.
Por ejemplo encontrar la ecuación de la parábola con vértice en el origen y foco F(1,0):
La parábola es horizontal y tiene de parámetro p=1 y se sustituye en y^2=4px i x=-p quedando y^2=4(1)x y x=-1 o y^2=4x y x+1=0, ecuación de la parábola y directriz.
Una circunferencia tiene su centro en el eje X y pasa por los puntos (-1,5) y (2,3) determina su ecuación
Encuentra la ecuación de la elipse con eje horizontal, centro en (3,−2) semieje mayor de 5 unidades y semieje menor de 3 unidades
Calcula la distancia focal de la elipse cuyos ejes miden 10 y 6 unidades
¿Cómo crees que estas formas geométricas pueden influir en el diseño arquitectónico contemporáneo?
determinar la ecuacion dela hiperbola c(4,3) semieje real 2 eje real paralelo de las absisas exentricidad 1,5
Hallar la ecuación de la hipérbola con c(4,3), semieje real 2, eje real paralelo a las absisas
Excentricidad e=1,5