Capítulos
Cuando hablamos de factorizar polinomios, hay varias características que tenemos que tener en cuenta.
Si no hay término independiente hay que sacar factor común. Sacar factor común de una suma (o resta) consiste en trasformarla en un producto.
Aplicaríamos la propiedad distributiva:
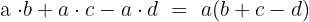
Ejemplo de factorización de polinomio sin termino independente
Descomponer en factores sacando factor común y hallar las raíces.
1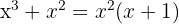 
La raíces son: 
y 
2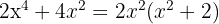 
Sólo tiene una raíz porque que el polinomio, 
, no tiene ningún valor que lo anule. Como la 
es al cuadrado, el resultado siempre será un número positivo, entonces es irreducible.
Doble extracción de factor común
1 
Sacamos factor común de y 
.
Como 
es ahora un factor común, sacamos factor común de .
La raíces son 
y 
.
Si tenemos un binomio
Cuando tenemos un binomio, puede ocurrir alguno de los siguientes casos:
Diferencia de cuadrados
Una diferencia de cuadrados es igual a suma por diferencia.
Ejemplos de ejercicios con diferencia de cuadrados:
Descomponer en factores y hallar las raíces
1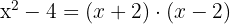 
Las raíces son 
y 
2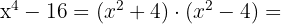 
El ultimo termino es también una diferencia de cuadrados, entonces:
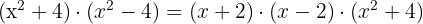
Las raíces son y
Suma de cubos
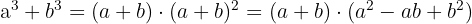
Ejemplo de ejercicio con suma de cubos:
Diferencia de cubos
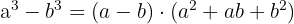
Ejemplo de ejercicio con diferencia de cubos :
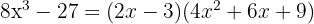
Si tenemos un trinomio
Cuando tenemos un trinomio, puede ocurrir alguno de los siguientes casos
Trinomio cuadrado perfecto
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado.
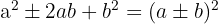
Ejemplos de trinomios cuadrados perfectos
Descomponer en factores y hallar las raíces
1 
Tenemos que preguntarnos:
- ¿Qué número elevado al cuadrado da
? La respuesta es 
? - ¿Qué número elevado al cuadrado da
?La respuesta es .
Y tenemos que comprobar que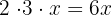 
La raíz es
, y se dice que es una raíz doble.
2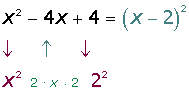 
- ¿Qué número elevado al cuadrado da ?
- ¿Qué número elevado al cuadrado da
? 
Y tenemos que comprobar que 
La raíz doble es 
.
Trinomio de segundo grado
Para descomponer en factores el trinomio de segundo grado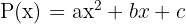 
, se iguala a cero y se resuelve la ecuación de segundo grado.
Si las soluciones a la ecuación son 
y 
, el polinomio descompuesto será:
Ejemplos de trinomios de segundo grado
Descomponer en factores y hallar las raíces
1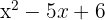 
Igualamos el trinomio a cero
Aplicamos la fórmula de la ecuación de segundo grado:
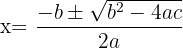
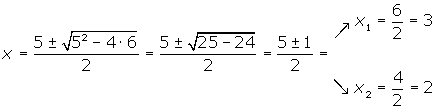
Factorizamos
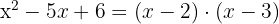
Las raíces son 
y .
2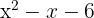 
Igualamos el trinomio a cero
Resolvemos la ecuación
Factorizamos
Las raíces son y .
Trinomios de cuarto grado de exponentes pares
Para hallar las raíces se iguala a cero y se resuelve la ecuación bicuadrada.
Ejemplos de trinomios de cuarto grado de exponentes partes
1 
Igualamos el polinomio a cero
Realizamos un cambio de variable
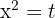
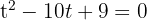
Resolvemos la ecuación de segundo grado
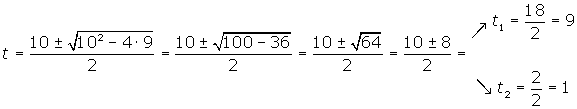
Deshacemos el cambio de variable y obtenemos las raíces
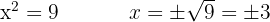
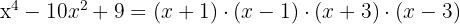
2 
Igualamos el polinomio a cero
Realizamos un cambio de variable
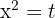
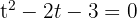
Resolvemos la ecuación de segundo grado
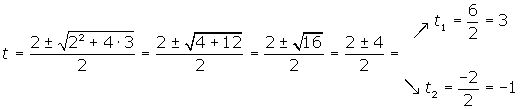
Deshacemos el cambio de variable y obtenemos las raíces
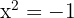, no tiene raíces reales, ya que no existe ningún número que elevado al cuadrado sea negativo
Se factoriza como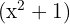 
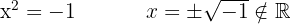
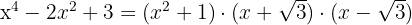
Factorización de un polinomio de grado superior a dos
Utilizamos el teorema del resto y la regla de Ruffini para encontrar las raíces enteras.
Los pasos a seguir los veremos con el polinomio:
Tomamos los divisores del término independiente: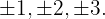
Aplicando el teorema del resto sabremos para qué valores la división es exacta.
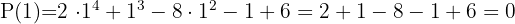
Dividimos por Ruffini.
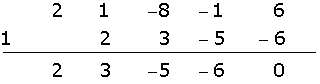
Por ser la división exacta, 
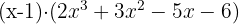
Una raíz es 
.
Continuamos realizando las mismas operaciones para encontrar el segundo factor.
Volvemos a probar por 
porque el primer factor podría estar elevado al cuadrado.
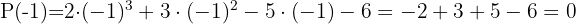
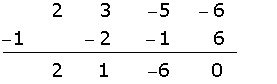
Otra raíz es 
.
El tercer factor lo podemos encontrar aplicando la ecuación de segundo grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar
raíces enteras.
El lo descartamos y seguimos probando por 
.
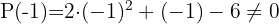
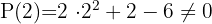
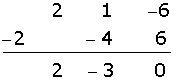
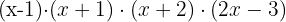
Sacamos factor común en último binomio y encontramos una raíz racional.
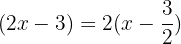
La factorización del polinomio queda:
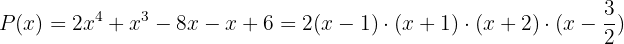
Raíces racionales
Puede suceder que el polinomio no tenga raíces enteras y sólo tenga raíces racionales. En este caso tomamos los divisores del término independiente dividido entre los divisores del término con mayor grado, y aplicamos el teorema del resto y la regla de Ruffini.
Probamos por:
.
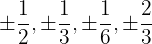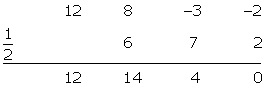
Factorizamos.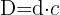 
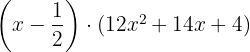
Volvemos a probar por 
Probamos por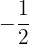 
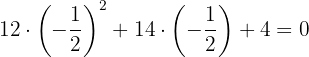
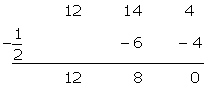
Factorizamos:
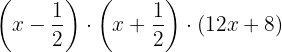
Sacamos factor común 
en el tercer factor.
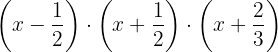
En Superprof puedes encontrar tu curso de matematicas.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado
Escribo y elijo bien las respuestas y me aparece el setenta porciento, no entiendo porque si todas me quedan bien.
Hola te agradecemos por visitar nuestra pagina, en cuanto a lo que pasa con los resultados del cuestionario, se supone que la pagina te da las respuestas de los ejercicios y allí puedes ver cual ejercicio tiene el error, podrías por favor indicárnoslo para rectificarlo.
– 2 no es raíz del último polunomio
Hola gracias por tus observaciones, podrías hacernos el favor de mencionar el número del ejercicio para poder rectificarlo, seria de gran ayuda.
(14m³×+21m²)÷(-7)