Capítulos

¿Qué estudia la combinatoria?
La combinatoria estudia los métodos para contar las distintas configuraciones de los elementos de un conjunto que cumplan ciertos criterios especificados.
En todo problema combinatorio hay varios conceptos claves que debemos distinguir:
1 Población
Es el conjunto de elementos que estamos estudiando. Denominaremos con  al número de elementos de este conjunto.
al número de elementos de este conjunto.
2 Muestra
Es un subconjunto de la población. Denominaremos con  al número de elementos que componen la muestra.
al número de elementos que componen la muestra.
Los diferentes tipos de muestra vienen determinados por dos aspectos:
Orden
Es decir, si es importante que los elementos de la muestra aparezcan ordenados o no.
Repetición
La posibilidad de repetición o no de los elementos.
Ejemplo:
En una clase de danza hay 10 alumnos y se quiere formar un comité de  personas que organice las presentaciones ¿De cuántas maneras distintas es esto posible?
personas que organice las presentaciones ¿De cuántas maneras distintas es esto posible?
Población: Los  alumnos
alumnos
Muestra: Un posible comité, por ejemplo: Ana, Rosa, Valeria y Carla.
¿Importa el orden en la muestra?
En este caso no, pues si ordenamos de diferente manera los elementos en nuestra muestra se obtiene el mismo comité.
Es decir, Ana, Rosa, Valeria y Carla forman el mismo comité que Carla, Rosa, Ana y Valeria.
¿Puede haber elementos repetidos en la muestra?
No, ya que se trata de personas, elementos que no se pueden repetir, y por ejemplo Ana, Ana, Rosa y Ana no se considera como un comité válido
Más adelante en el estudio de las técnicas de combinatoria podrás ver que la respuesta a esta pregunta es:

Factorial de un número
Es el producto de los  factores consecutivos desde
factores consecutivos desde  hasta
hasta  . El factorial de un número natural se denota por
. El factorial de un número natural se denota por 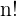 .
.
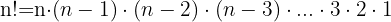
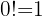
Ejemplo:
Calcular el factorial de  .
.
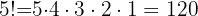
Principio fundamental de conteo
Si cierta tarea puede realizarse de  maneras diferentes y, para cada una de esas formas, una segunda tarea puede realizarse de
maneras diferentes y, para cada una de esas formas, una segunda tarea puede realizarse de  maneras distintas, entonces las dos tareas puede realizarse de
maneras distintas, entonces las dos tareas puede realizarse de 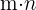 formas distintas.
formas distintas.
Ejemplos:
- Si tengo
 playeras y
playeras y  pantalones diferentes ¿De cuántas maneras diferentes me puedo vestir?
pantalones diferentes ¿De cuántas maneras diferentes me puedo vestir?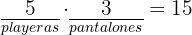
- ¿Cuántos números naturales de
 o menos cifras hay?
o menos cifras hay? - La respuesta es sencilla: Hay
 números, pues son todos los números enteros del
números, pues son todos los números enteros del  al
al 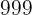 .
.
Sin embargo podemos pensarlo de la siguientes manera:
Números de a lo más una cifra hay :
: y
y  .Para contar los de hasta dos cifras (
.Para contar los de hasta dos cifras ( al
al  ), no hace falta escribirlos todos, basta con observar que la primera cifra puede ser cualquiera de los
), no hace falta escribirlos todos, basta con observar que la primera cifra puede ser cualquiera de los  dígitos
dígitos 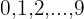 , y por cada uno de estos hay 10 terminaciones distintas; por ejemplo los números que comienzan con
, y por cada uno de estos hay 10 terminaciones distintas; por ejemplo los números que comienzan con  son:
son:  , diez en total.Así, la cantidad de enteros de a lo más dos cifras es:
, diez en total.Así, la cantidad de enteros de a lo más dos cifras es: 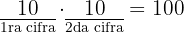
Para contar los números de a lo más 3 cifras se hace de manera similar:
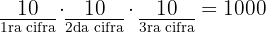
Técnicas para contar arreglos
Además del principio básico de conteo, hay otras técnicas para contar arreglos.
Superprof tiene un artículo con el listado de las herramientas principales en combinatoria:
Cada una de las mencionadas cuenta con un artículo independiente en el que se detalla su uso:
- Combinaciones
- Combinaciones con repetición
- Permutaciones
- Permutaciones con repetición
- Permutaciones circulares
- Variaciones
- Variaciones con repetición
Y otros temas relacionados:
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3