Antes de empezar los ejercicios y problemas de probabilidad condicionada, no dudes en echar un ojo a nuestra teoría con el resumen de probabilidades.
El 30% de los alumnos estudia inglés y francés mientras que el 60% estudia francés. Encuentra la probabilidad de que un alumno que estudia francés, también estudie inglés
1 Indicamos los eventos
F: el alumno estudia francés.
I: el alumno estudia inglés.
2 Sabemos que
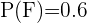
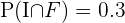
3 Calculamos la probabilidad de que un alumno que estudia francés, también estudie inglés
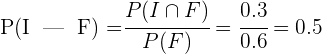
El 47% de los amigos de Juan tienen una consola de Nintendo y X box, mientras que el 70% tiene X box. Encuentra la probabilidad de que un amigo de Juan que tiene X box, también tenga una consola de Nintendo
1 Indicamos los eventos
N: el amigo tiene consola de Nintendo.
X: el amigo tiene consola de X box.
2 Sabemos que
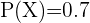
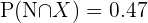
3 Calculamos la probabilidad de que un amigo de Juan que tiene consola de X box, también tenga consola de Nintendo
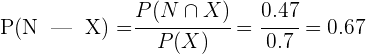
El 30% de los alumnos aprobó el examen de matemáticas y el 15% aprobó química y matemáticas. Encuentra la probabilidad de que un alumno que aprobó matemáticas, también apruebe química
1 Indicamos los eventos
M: el alumno aprobó matemáticas.
Q: el alumno aprobó química.
2 Sabemos que

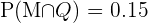
3 Calculamos la probabilidad de que un alumno que aprobó matemáticas, también apruebe química
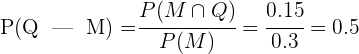
En una institución el 75% de las personas juega futbol. Si el 20% de las personas además de jugar futbol también juegan beisbol, ¿cual es la probabilidad de que una persona de la institución que juega futbol, también juegue beisbol?
1 Indicamos los eventos
F: juega futbol.
B: juega beisbol.
2 Sabemos que
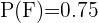
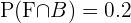
3 Calculamos la probabilidad de que una persona que juega futbol también juegue beisbol
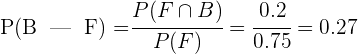
Una urna contiene 3 bolas rojas, 2 verdes y 1 azul. Se saca una bola y sin devolverla a la bolsa se saca otra bola. ¿Cuál es la probabilidad de que la segunda bola sea roja si la primera es azul?
En total se tiene 6 bolas. Si la primera en salir es azul, entonces en total quedan 5 bolas, de las cuales 3 son rojas. Así la probabilidad de sacar una bola roja es
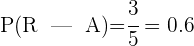
Una urna contiene 4 bolas rojas, 2 verdes y 4 azules. Se saca una bola y sin devolverla a la bolsa se saca otra bola. ¿Cuál es la probabilidad de que la segunda bola sea verde si la primera es roja?
En total se tiene 10 bolas. Si la primera en salir es roja, entonces en total quedan 9 bolas, de las cuales 2 son verdes. Así la probabilidad de sacar una bola verde es
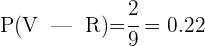
Una urna contiene 3 bolas rojas, 2 verdes y 4 azules. Se saca una bola y sin devolverla a la bolsa se saca otra bola. ¿Cuál es la probabilidad de que la segunda bola sea roja si la primera también es roja?
En total se tiene 9 bolas. Si la primera en salir es roja, entonces en total quedan 8 bolas, de las cuales 2 son rojas. Así la probabilidad de sacar una bola verde es
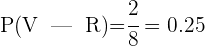
De una baraja de  cartas se extraen simultáneamente dos de ellas. Calcular la probabilidad de que:
cartas se extraen simultáneamente dos de ellas. Calcular la probabilidad de que:
aLas dos sean copas
bAl menos una sea copa
cUna sea copa y la otra espada
a Las dos sean copas
Podemos tratar este problema como si realizáramos dos extracciones sin reemplazo.
Denotemos por  al evento de obtener una copa en la extracción
al evento de obtener una copa en la extracción  -ésima, con
-ésima, con 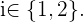 Con esto en mente y de acuerdo con la definición de probabilidad condicional
Con esto en mente y de acuerdo con la definición de probabilidad condicional
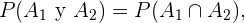
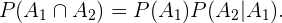
Para calcular 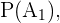 simplemente dividimos el número de casos favorables entre el número de casos totales. En este caso hay 12 posibles cartas de copas, es decir 12 es el número de casos favorables, y un total de 48 cartas, que representan el número de casos totales. Entonces
simplemente dividimos el número de casos favorables entre el número de casos totales. En este caso hay 12 posibles cartas de copas, es decir 12 es el número de casos favorables, y un total de 48 cartas, que representan el número de casos totales. Entonces

Por otro lado,
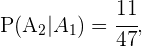
pues el número de casos favorables es 11, al haber extraído ya una copa, y el total de cartas es ahora 47.
Luego,

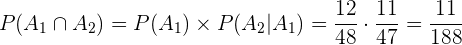
b Al menos una sea copa
Denotamos por  al evento de obtener una copa en la extracción
al evento de obtener una copa en la extracción 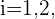 y por
y por 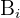 al evento de no obtener una copa en la extracción
al evento de no obtener una copa en la extracción  La condición de extraer al menos una copa se satisface en cualquiera de los siguientes casos
La condición de extraer al menos una copa se satisface en cualquiera de los siguientes casos
se obtiene una copa en ambas extracciones,
se obtiene una copa en la primera extracción y no se obtiene copa en la segunda, y
no se obtiene una copa en la primera extracción y se obtiene una copa en la segunda.
Entonces la probabilidad solicitada será la probabilidad de la union de los tres eventos anteriores, que es equivalente a la suma de sus probabilidades, pues son eventos ajenos entre sí. En términos matemáticos esto es
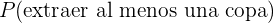
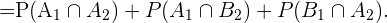
Por el inciso anterior sabemos que 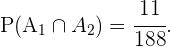
Para calcular las probabilidades restantes haremos uso de la probabilidad condicional. Obtenemos
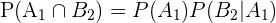

El número de casos favorables en el evento 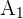 es 12 y en el evento
es 12 y en el evento 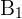 es 36, pues es el número de cartas que no son copas. En ambos casos, al ser la primera extracción, el número de casos totales sigue siendo 48. Por lo tanto
es 36, pues es el número de cartas que no son copas. En ambos casos, al ser la primera extracción, el número de casos totales sigue siendo 48. Por lo tanto
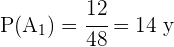
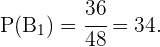
Luego, el número de casos favorables en el evento 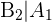 son 36, ya que es el número de cartas que no son copas; mientras que para
son 36, ya que es el número de cartas que no son copas; mientras que para 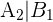 son 12, pues aún no se ha extraído ninguna copa. En ambos casos, el número de casos totales es 47, pensando en que hemos sacado ya una carta. Por lo tanto
son 12, pues aún no se ha extraído ninguna copa. En ambos casos, el número de casos totales es 47, pensando en que hemos sacado ya una carta. Por lo tanto

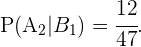
Entonces
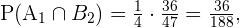
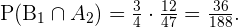
Y así,

c Una sea copa y la otra espada
Llamemos  al evento de obtener una copa en la extracción
al evento de obtener una copa en la extracción 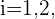 y como
y como 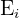 al evento de no obtener una espada en la extracción
al evento de no obtener una espada en la extracción  La condición de extraer una copa y una espada se satisface en cualquiera de los siguientes casos
La condición de extraer una copa y una espada se satisface en cualquiera de los siguientes casos
se obtiene una copa en la primera extracción y una espada en la segunda, y
se obtiene una espada en la primera extracción y una copa en la segunda.
Entonces la probabilidad que buscamos será la probabilidad de la union de los tres eventos anteriores, que es equivalente a la suma de sus probabilidades, pues son eventos ajenos entre sí. En términos matemáticos esto es
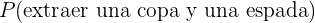
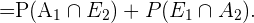
Y a su vez,
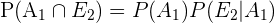
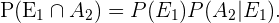
Como hay 12 cartas de cada palo en la baraja, y la baraja tiene un total de 48 cartas, usando la fórmula de número de casos favorables entre casos totales, se sigue que
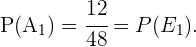
Por otro lado, en el caso del evento 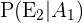 tenemos 12 casos favorables y un total de 47 cartas (pues ya se ha realizado una extracción) o casos totales. Notemos que son las mismas cuentas para
tenemos 12 casos favorables y un total de 47 cartas (pues ya se ha realizado una extracción) o casos totales. Notemos que son las mismas cuentas para 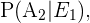 por tanto
por tanto
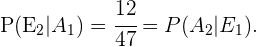
Con lo anterior, obtenemos
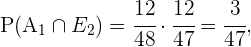

Finalmente,
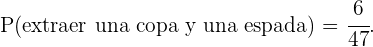
Ante un examen, un alumno sólo ha estudiado  de los
de los  temas correspondientes a la materia del mismo. Éste se realiza en trayendo al azar dos temas y dejando que el alumno escoja uno de los dos para ser examinado del mismo. Hallar la probabilidad de que el alumno pueda elegir en el examen uno de los temas estudiados
temas correspondientes a la materia del mismo. Éste se realiza en trayendo al azar dos temas y dejando que el alumno escoja uno de los dos para ser examinado del mismo. Hallar la probabilidad de que el alumno pueda elegir en el examen uno de los temas estudiados
Llamemos  al evento "el alumno puede elegir durante el examen uno de los temas estudiados". Entonces se tiene que
al evento "el alumno puede elegir durante el examen uno de los temas estudiados". Entonces se tiene que

donde 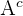 denota al evento complementario de
denota al evento complementario de  es decir "el alumno no puede elegir durante el examen uno de los temas estudiados".
es decir "el alumno no puede elegir durante el examen uno de los temas estudiados".
Para calcular 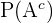 notemos que hay 10 temas para los cuales el alumno no ha estudiado, por lo que la probabilidad de elegir como primer tema uno de éstos es igual a
notemos que hay 10 temas para los cuales el alumno no ha estudiado, por lo que la probabilidad de elegir como primer tema uno de éstos es igual a 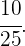 Simplemente hemos aplicado la regla
Simplemente hemos aplicado la regla

De la misma manera, la probabilidad de elegir como segundo tema alguno que el alumno no ha estudiado es 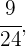 pues en este caso ya hemos elegido con anterioridad un tema no estudiado y eso nos deja
pues en este caso ya hemos elegido con anterioridad un tema no estudiado y eso nos deja  posibles casos favorables y
posibles casos favorables y  casos totales.
casos totales.
Luego, el resultado de 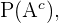 es multiplicar las dos probabilidades que hemos encontrado pues asumimos que es equivalente a extraer sin reemplazo dos temas no estudiados, por tanto
es multiplicar las dos probabilidades que hemos encontrado pues asumimos que es equivalente a extraer sin reemplazo dos temas no estudiados, por tanto

Entonces,
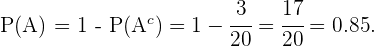
Una clase está formada por  chicos y
chicos y  chicas; la mitad de las chicas y la mitad de los chicos han elegido francés como asignatura optativa.
chicas; la mitad de las chicas y la mitad de los chicos han elegido francés como asignatura optativa.
a¿Cuál es la probabilidad de que una persona elegida al azar sea chico o estudio francés?
b¿Y la probabilidad de que sea chica y no estudie francés?
a ¿Cuál es la probabilidad de que una persona elegida al azar sea chico o estudio francés?

Llamemos  al evento "la persona elegida al azar es chico y no ha elegido francés" y
al evento "la persona elegida al azar es chico y no ha elegido francés" y  al evento "la person elegida al azar estudia francés". Entonces, si
al evento "la person elegida al azar estudia francés". Entonces, si  denota el evento "la persona elegida al azar es chico o estudia francés", es la probabilidad que deseamos calcular y
denota el evento "la persona elegida al azar es chico o estudia francés", es la probabilidad que deseamos calcular y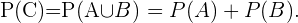
La última igualdad es cierta debido a que los eventos  y
y  son ajenos.
son ajenos.
Para calcular  aplicaremos la regla
aplicaremos la regla
En el evento  el número de casos favorables es
el número de casos favorables es  pues este es el número de personas que cumplen con ser chicos y no estudiar francés; mientras que para
pues este es el número de personas que cumplen con ser chicos y no estudiar francés; mientras que para  el número de personas que estudia francés es igual a
el número de personas que estudia francés es igual a  que es el número de casos favorables. En ambos eventos el número de casos totales es
que es el número de casos favorables. En ambos eventos el número de casos totales es 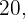 que es el total número de alumnos. Con esto podemos concluir que
que es el total número de alumnos. Con esto podemos concluir que
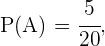
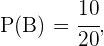
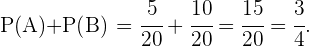
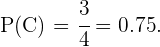
b ¿Y la probabilidad de que sea chica y no estudié francés?
En el contexto del inciso anterior, basta observar que el evento "elegir al azar una chica que no estudie francés" es equivalente a  o sea, es el evento complementario de
o sea, es el evento complementario de 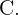
Para cualquier evento y su complemento, las siguientes igualdades son válidas debido a que éstos siempre son ajenos.
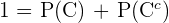
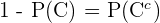
Entonces, sustituyendo el valor que encontramos en el inciso anterior para

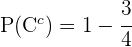
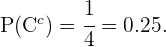
En una clase en la que todos practican algún deporte, el  % de los alumnos juega al fútbol o al baloncesto y el
% de los alumnos juega al fútbol o al baloncesto y el  % practica ambos deportes. Si además hay un
% practica ambos deportes. Si además hay un  % que no juega al fútbol, ¿cuál será la probabilidad de que escogido al azar un alumno de la clase:
% que no juega al fútbol, ¿cuál será la probabilidad de que escogido al azar un alumno de la clase:
aJuegue sólo al fútbol
bJuegue sólo al baloncesto
cPractique uno solo de los deportes
dNo juegue ni al fútbol ni al baloncesto
a Juegue sólo al fútbol
Tenemos que el 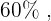 de los alumnos juega fútbol o baloncesto y de dicho porcentaje, hay un
de los alumnos juega fútbol o baloncesto y de dicho porcentaje, hay un 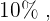   que practica ambos deportes. Esto quiere decir que el
  que practica ambos deportes. Esto quiere decir que el  de los alumnos juegan solo uno de los deportes, lo cual significa que la probabilidad de elegir a un alumno que juegue solo uno de los deportes es igual a .5.
de los alumnos juegan solo uno de los deportes, lo cual significa que la probabilidad de elegir a un alumno que juegue solo uno de los deportes es igual a .5.
Por otro lado, el 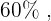 o con probabilidad
o con probabilidad 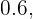 , no juega fútbol. Esto quiere decir que del
, no juega fútbol. Esto quiere decir que del  que juegan solo un deporte, el
que juegan solo un deporte, el 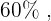 juega solo baloncesto. Ahora, el
juega solo baloncesto. Ahora, el 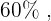 del
del  lo encontramos haciendo el producto
lo encontramos haciendo el producto 
Por lo tanto, si  es el evento "jugar solo fútbol" y
es el evento "jugar solo fútbol" y  "jugar solo baloncesto", y
"jugar solo baloncesto", y  "juega solo uno de los deportes", se sigue que
"juega solo uno de los deportes", se sigue que
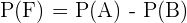
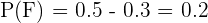
b Juegue sólo al baloncesto
Tenemos que el 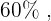 de los alumnos juega fútbol o baloncesto y de dicho porcentaje, hay un
de los alumnos juega fútbol o baloncesto y de dicho porcentaje, hay un 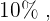   que practica ambos deportes. Esto quiere decir que el
  que practica ambos deportes. Esto quiere decir que el  de los alumnos juegan solo uno de los deportes, lo cual significa que la probabilidad de elegir a un alumno que juegue solo uno de los deportes es igual a .5.
de los alumnos juegan solo uno de los deportes, lo cual significa que la probabilidad de elegir a un alumno que juegue solo uno de los deportes es igual a .5.
Por otro lado, el 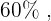 o con probabilidad
o con probabilidad 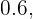 , no juega fútbol. Esto quiere decir que del
, no juega fútbol. Esto quiere decir que del  que juegan solo un deporte, el
que juegan solo un deporte, el 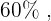 juega solo baloncesto. Ahora, el
juega solo baloncesto. Ahora, el 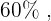 del
del  lo encontramos haciendo el producto
lo encontramos haciendo el producto 
Por lo tanto, si  es el evento "jugar solo baloncesto", entonces
es el evento "jugar solo baloncesto", entonces 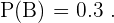
c Practique uno solo de los deportes
Tenemos que el 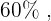 de los alumnos juega fútbol o baloncesto y de dicho porcentaje, hay un
de los alumnos juega fútbol o baloncesto y de dicho porcentaje, hay un 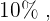   que practica ambos deportes. Esto quiere decir que el
  que practica ambos deportes. Esto quiere decir que el  de los alumnos juegan solo uno de los deportes, lo cual significa que la probabilidad de elegir a un alumno que juegue solo uno de los deportes es igual a 0.5.
de los alumnos juegan solo uno de los deportes, lo cual significa que la probabilidad de elegir a un alumno que juegue solo uno de los deportes es igual a 0.5.
d No juegue ni al fútbol ni al baloncesto
Llamemos  al evento "juegan futbol" y
al evento "juegan futbol" y  al evento "juegan baloncesto". Entonces "jugar fútbol o jugar baloncesto" es equivalente al evento
al evento "juegan baloncesto". Entonces "jugar fútbol o jugar baloncesto" es equivalente al evento 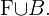 Entonces, la probabilidad de elegir a alguien que no juegue al fútbol es igual a la probabilidad del evento complemento de
Entonces, la probabilidad de elegir a alguien que no juegue al fútbol es igual a la probabilidad del evento complemento de 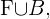 del cual sí conocemos la probabilidad, pues por hipótesis
del cual sí conocemos la probabilidad, pues por hipótesis 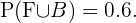
Luego

Un taller sabe que por término medio acuden: por la mañana tres automóviles con problemas eléctricos, ocho con problemas mecánicos y tres con problemas de chapa, y por la tarde dos con problemas eléctricos, tres con problemas mecánicos y uno con problemas de chapa.
aHacer una tabla ordenando los datos anteriores
bCalcular el porcentaje de los que acuden por la tarde
cCalcular el porcentaje de los que acuden por problemas mecánicos
dCalcular la probabilidad de que un automóvil con problemas eléctricos acuda por la mañana
a Hacer una tabla ordenando los datos anteriores
| Horario | Problema eléctrico | Problema mecánicos | Problema de chapa |
|---|---|---|---|
| Matutino | 3 | 8 | 3 |
| Vespertino | 2 | 3 | 1 |
b Calcular el porcentaje de los que acuden por la tarde
Para calcular el porcentaje de los autos que acuden por la tarde, simplemente tenemos que encontrar el cociente

Para esta situación, el número de casos favorables es el número de autos que asisten por la tarde al taller, es decir, 6; mientras que el número de casos totales es el total de autos que se presentan, o sea 20. Por lo tanto,
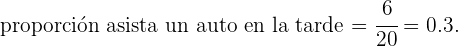
Finalmente, para expresar esta cifra en porcentaje, solamente la hemos de multiplicar por cien. Entonces el porcentaje de autos que asisten por la tarde es 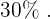
c Calcular el porcentaje de los que acuden por problemas mecánicos
Para calcular el porcentaje de los autos que acuden por la tarde, simplemente tenemos que encontrar el cociente

Para esta situación, el número de casos favorables es el número total de autos que asisten al taller por problemas mecánicos, es decir 11; mientras que el número de casos totales es el total de autos que se presentan, o sea 20. Por lo tanto,
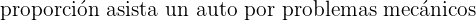
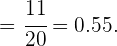
Finalmente, para expresar esta cifra en porcentaje, solamente la hemos de multiplicar por cien. Entonces el porcentaje de autos que asisten por la tarde es 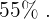
d Calcular la probabilidad de que un automóvil con problemas eléctricos acuda por la mañana
Para calcular el porcentaje de los autos que acuden por problemas eléctricos, simplemente tenemos que encontrar el cociente

Para esta situación, el número de casos favorables es el número total de autos que asisten al taller por problemas eléctricos durante el turno matutino, es decir 3; mientras que el número de casos totales es el total de autos que se presentan por problemas eléctricos, o sea 5. Por lo tanto,
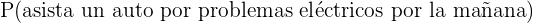

En una ciudad, el  de la población tiene cabellos castaños, el
de la población tiene cabellos castaños, el  tiene ojos castaños y el
tiene ojos castaños y el  tiene cabellos y ojos castaños. Se escoge una persona al azar:
tiene cabellos y ojos castaños. Se escoge una persona al azar:
aSi tiene los cabellos castaños, ¿Cuál es la probabilidad de que tenga también ojos castaños?
bSi tiene ojos castaños, ¿Cuál es la probabilidad de que no tenga cabellos castaños?
c¿Cuál es la probabilidad de que no tenga cabellos ni ojos castaños?
a Si tiene los cabellos castaños, ¿Cuál es la probabilidad de que tenga también ojos castaños?


Denotemos mediante  a los eventos "tener ojos castaños" y "tener cabello castaño" respectivamente. Así, la probabilidad que estamos buscando queda expresada como
a los eventos "tener ojos castaños" y "tener cabello castaño" respectivamente. Así, la probabilidad que estamos buscando queda expresada como 
Y por la definición de probabilidad condicional, esto es
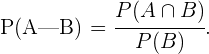
Observermos que 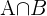 es equivalente a "tener ojos castaños y cabello castaño", del cual conocemos su probabilidad pues el
es equivalente a "tener ojos castaños y cabello castaño", del cual conocemos su probabilidad pues el  cumple esta condición, lo cual quiere decir que
cumple esta condición, lo cual quiere decir que 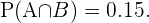 Siguiendo un razonamiento similar, tenemos que
Siguiendo un razonamiento similar, tenemos que 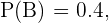 por lo tanto
por lo tanto
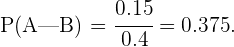
2 Si tiene ojos castaños, ¿Cuál es la probabilidad de que no tenga cabellos castaños?
De acuerdo al planteamiento del problema, el  tiene ojos castaños y además el
tiene ojos castaños y además el  tiene cabellos y ojos castaños, de aquí se sigue que el
tiene cabellos y ojos castaños, de aquí se sigue que el  restante debe tener ojos castaños pero no cabellos castaños.
restante debe tener ojos castaños pero no cabellos castaños.
Haciendo  los eventos "no tener cabellos castaños" y "tener ojos castaños" respectivamente, entonces se sigue del párrafo anterior que el evento
los eventos "no tener cabellos castaños" y "tener ojos castaños" respectivamente, entonces se sigue del párrafo anterior que el evento 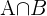 (equivalente a "tener ojos castaños y no tener cabellos castaños) tiene probabilidad de
(equivalente a "tener ojos castaños y no tener cabellos castaños) tiene probabilidad de  Como además sabemos que el
Como además sabemos que el  tiene ojos castaños, entonces
tiene ojos castaños, entonces 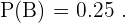
Luego, de la definición de probabilidad condicional
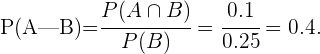
c ¿Cuál es la probabilidad de que no tenga cabellos ni ojos castaños?
De acuerdo al planteamiento del problema, el  tiene ojos castaños y además el
tiene ojos castaños y además el  tiene cabellos y ojos castaños, de aquí se sigue que el
tiene cabellos y ojos castaños, de aquí se sigue que el  restante debe tener ojos castaños pero no cabellos castaños.
restante debe tener ojos castaños pero no cabellos castaños.
Por otro lado sabemos que el  de la población tiene cabellos castaños, de donde podemos inferir que el
de la población tiene cabellos castaños, de donde podemos inferir que el  restante no tiene cabellos castaños. Adicional a esto, hemos encontrado que el
restante no tiene cabellos castaños. Adicional a esto, hemos encontrado que el  no tiene cabellos castaños pero si ojos castaños, entonces restándolos al porcentaje total de población sin cabellos castaños, obtenemos que el
no tiene cabellos castaños pero si ojos castaños, entonces restándolos al porcentaje total de población sin cabellos castaños, obtenemos que el  de la población no tiene ni cabellos ni ojos castaños. Por lo tanto la probabilidad de elegir a una persona sin cabellos castaños y sin ojos castaños es de
de la población no tiene ni cabellos ni ojos castaños. Por lo tanto la probabilidad de elegir a una persona sin cabellos castaños y sin ojos castaños es de 
En un aula hay  alumnos, de los cuales:
alumnos, de los cuales:  son hombres,
son hombres,  usan gafas, y
usan gafas, y  son varones y usan gafas.
son varones y usan gafas.
a¿Cuál es la probabilidad de que sea mujer y no use gafas?
bSi sabemos que el alumno seleccionado no usa gafas, ¿Qué probabilidad hay de que sea hombre?
a ¿Cuál es la probabilidad de que sea mujer y no use gafas?
Tenemos 100 alumnos, de los cuales 40 son hombres, lo cual significa que 60 son mujeres. Además 30 alumnos utilizan gafas y 15 de ellos son varones, lo cual indica que los otros 15 alumnos con gafas son mujeres. Luego, tenemos 25 hombres sin gafas y 45 mujeres sin gafas.
Luego, la probabilidad de que sea mujer y no use gafas la podemos encontrar mediante la regla

En este caso el número de casos favorables es el número de mujeres que no usan gafas, o sea 45, mientras que el número de casos totales es el total de alumnos. Entonces,

b Si sabemos que el alumno seleccionado no usa gafas, ¿Qué probabilidad hay de que sea hombre?
Sean  los eventos "ser varón" y "no usar gafas" respectivamente. Así, la probabilidad que buscamos está dada por
los eventos "ser varón" y "no usar gafas" respectivamente. Así, la probabilidad que buscamos está dada por 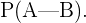
Tenemos entonces que 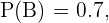 pues 70 de los cien alumnos no usan gafas, es decir
pues 70 de los cien alumnos no usan gafas, es decir

Por otro lado  es equivalente al evento "ser hombre y no usar gafas", y de acuerdo al ejercicio anterior hay 25 alumnos que se encuentran dentro de de esta categoría, por lo que
es equivalente al evento "ser hombre y no usar gafas", y de acuerdo al ejercicio anterior hay 25 alumnos que se encuentran dentro de de esta categoría, por lo que
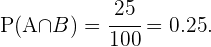
Siguiendo la definición de probabilidad condicional, tenemos que
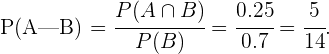
Se sortea un viaje a Roma entre los  mejores clientes de una agencia de automóviles. De ellos,
mejores clientes de una agencia de automóviles. De ellos,  son mujeres,
son mujeres,  están casados y
están casados y  son mujeres casadas. Se pide:
son mujeres casadas. Se pide:
a¿Cuál será la probabilidad de que le toque el viaje a un hombre soltero?
bSi del afortunado se sabe que es casado, ¿Cuál será la probabilidad de que sea una mujer?
a ¿Cuál será la probabilidad de que le toque el viaje a un hombre soltero?
Comencemos notando que dentro de la población tenemos 65 mujeres y 55 hombres, pues la suma de individuos debe ser de 120. Continuando con el mismo razonamiento, sabemos que hay 80 personas casadas y 45 de ellas son mujeres, lo cual nos deja con 35 hombres casados y 20 solteros.
Por lo tanto, la probabilidad de que el viaje que se sortea le toque a un hombre soltero es de
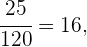
donde simplemente hemos aplicado la regla

e identificado a los casos favorables como los hombres solteros y los casos totales como el número total de individuos con los que se hará la rifa.
b Si del afortunado se sabe que es casado, ¿Cuál será la probabilidad de que sea una mujer?
En el ejercicio anterior, calculamos el número de mujeres casadas, el cual asciende a 45. Sabiendo que hay 80 personas casadas, la probabilidad de que el viaje sea para una mujer, sabiendo que el afortunado es casado, es


En este caso el número de casos totales es el número de individuos casados, ya que sabemos que el ganador del viaje se lo ha ganado una persona casada. Mientras que el número de casos favorables son las mujeres casadas.
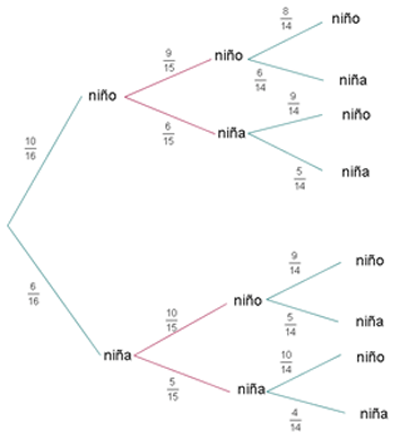
Una clase consta de seis niñas y  niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:
niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:
aSeleccionar tres niños
bSeleccionar exactamente dos niños y una niña
cSeleccionar por lo menos un niño
dSeleccionar exactamente dos niñas y un niño
a Seleccionar tres niños
Podemos tratar este problema como si realizáramos dos extracciones sin reemplazo.
Denotemos por  al evento de elegir a un niño en la extracción
al evento de elegir a un niño en la extracción  -ésima, con
-ésima, con 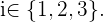 Con esto en mente y de acuerdo con la definición de probabilidad condicional
Con esto en mente y de acuerdo con la definición de probabilidad condicional
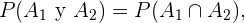
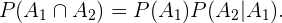
Para calcular 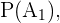 simplemente dividimos el número de casos favorables entre el número de casos totales. En este caso hay 10 posibles niños a elegir, es decir 10 es el número de casos favorables, y un total de 16 niños, que representan el número de casos totales. Entonces
simplemente dividimos el número de casos favorables entre el número de casos totales. En este caso hay 10 posibles niños a elegir, es decir 10 es el número de casos favorables, y un total de 16 niños, que representan el número de casos totales. Entonces
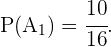
Por otro lado,
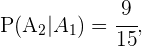
pues el número de casos favorables es 9, al haber elegido ya a un niño, y el total de niños por elegir es ahora 15.
Luego,
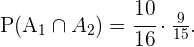
Aplicando este argumento manera iterativa para la elección del tercer niño tendríamos que
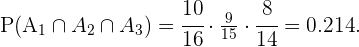
b Seleccionar exactamente dos niños y una niña
Para calcular esta probabilidad, primero necesitamos identificar los diferentes casos en los que podríamos seleccionar dos niños y una niña. El primer caso es elegir 2 niños y al final una niña, el segundo caso es elegir una niña y al final dos niños, y por último un niño, una niña y un niño. La probabilidad de cada caso la podemos calcular haciendo la multiplicación de la probabilidad en cada paso de la figura presentada en el inicio.
Por ejemplo, si el primer caso lo denotamos como evento  entonces
entonces
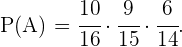
Luego, denotando como 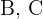 a los eventos restantes, tenemos que
a los eventos restantes, tenemos que
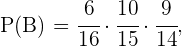
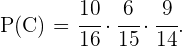
Finalmente, la probabilidad que estamos buscando es la probabilidad de que cualquiera de estos eventos suceda, o sea 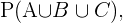 como éstos son ajenos se sigue que
como éstos son ajenos se sigue que
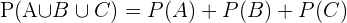
Por lo tanto,
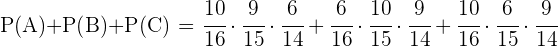

c Seleccionar por lo menos un niño
Para calcular la probabilidad de seleccionar al menos un niño, haremos
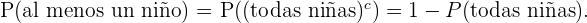
Podemos calcular la probabilidad de elegir tres niñas de manera completamente análoga al inciso uno de este mismo ejercicio. Entonces
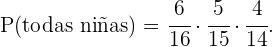
Luego,
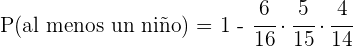
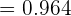
d Seleccionar exactamente dos niñas y un niño
Para calcular esta probabilidad, primero necesitamos identificar los diferentes casos en los que podríamos seleccionar dos niñas y una niño. El primer caso es elegir 2 niñas y al final un niño, el segundo caso es elegir un niño y al final dos niñas, y por último una niña, un niño y una niña. La probabilidad de cada caso la podemos calcular haciendo la multiplicación de la probabilidad en cada paso de la figura presentada en el inicio.
Por ejemplo, si el primer caso lo denotamos como evento  entonces
entonces
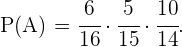
Luego, denotando como 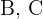 a los eventos restantes, tenemos que
a los eventos restantes, tenemos que
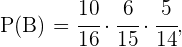
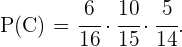
Finalmente, la probabilidad que estamos buscando es la probabilidad de que cualquiera de estos eventos suceda, o sea 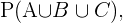 como éstos son ajenos se sigue que
como éstos son ajenos se sigue que
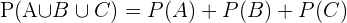
Por lo tanto,
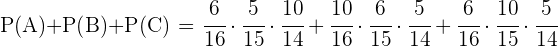
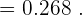
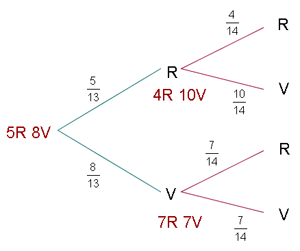
Una urna contiene  bolas rojas y
bolas rojas y  verdes. Se extrae una bola y se reemplaza por dos del otro color. A continuación, se extrae una segunda bola
verdes. Se extrae una bola y se reemplaza por dos del otro color. A continuación, se extrae una segunda bola
aProbabilidad de que la segunda bola sea verde
bProbabilidad de que las dos bolas extraídas sean del mismo color
a Probabilidad de que la segunda bola sea verde
Sea  el evento "la segunda bola es verde", hay dos posibilidades para dicho evento, que la primera bola sea roja o que la primera bola sea verde. Representaremos lo anterior como
el evento "la segunda bola es verde", hay dos posibilidades para dicho evento, que la primera bola sea roja o que la primera bola sea verde. Representaremos lo anterior como 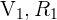 y es importante observar que éstos casos son mutuamente excluyentes, es decir no pueden ocurrir ambos a la vez. Por lo tanto,
y es importante observar que éstos casos son mutuamente excluyentes, es decir no pueden ocurrir ambos a la vez. Por lo tanto,
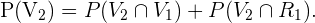
Siguiendo la definición de probabilidad de una intersección, tenemos que
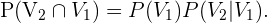
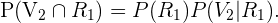
De acuerdo al diagrama presentado al inicio de la solución,

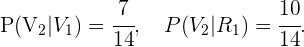
Con esto, obtenemos que

b Probabilidad de que las dos bolas extraídas sean del mismo color
Sean 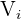 el evento "la bola i-ésima es verde", y
el evento "la bola i-ésima es verde", y  el evento "la bola i-ésima es roja", buscamos
el evento "la bola i-ésima es roja", buscamos 
Siguiendo la definición de probabilidad de una intersección, tenemos que
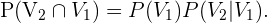

De acuerdo al diagrama presentado al inicio de la solución,


Con esto, obtenemos que
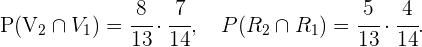
Se supone que  de cada
de cada  hombres y
hombres y  de cada
de cada  mujeres usan gafas. Si el número de mujeres es cuatro veces superior al de hombres, se pide la probabilidad de encontrarnos:
mujeres usan gafas. Si el número de mujeres es cuatro veces superior al de hombres, se pide la probabilidad de encontrarnos:
aCon una persona sin gafas
bCon una mujer con gafas
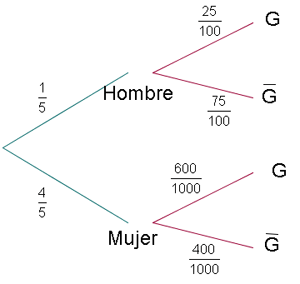
a Con una persona sin gafas
Del total de la población, sabemos que  corresponde a la proporción de mujeres y
corresponde a la proporción de mujeres y  corresponde a la proporción de los hombres. De esta manera se cumple la condición "el número de mujeres es cuatro veces superior al de hombres".
corresponde a la proporción de los hombres. De esta manera se cumple la condición "el número de mujeres es cuatro veces superior al de hombres".
Luego, 25 de cada 100 hombres usan gafas es equivalente a que 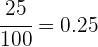 es la probabilidad de encontrarnos a un hombre con gafas, de donde se sigue que el
es la probabilidad de encontrarnos a un hombre con gafas, de donde se sigue que el  es la probabilidad para los hombres que no usan gafas. Bajo el mismo razonamiento,
es la probabilidad para los hombres que no usan gafas. Bajo el mismo razonamiento,  es la probabilidad de encontrarnos a una mujer con gafas, mientras que
es la probabilidad de encontrarnos a una mujer con gafas, mientras que  es la probabilidad para las mujeres sin gafas. En ambos casos, solamente hemos calculado el cociente de los casos favorables entre los casos totales.
es la probabilidad para las mujeres sin gafas. En ambos casos, solamente hemos calculado el cociente de los casos favorables entre los casos totales.
Sean  los eventos "no tener gafas", "ser hombre" y "ser mujer" respectivamente, estamos buscando
los eventos "no tener gafas", "ser hombre" y "ser mujer" respectivamente, estamos buscando 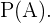 Como ser hombre y ser mujer son eventos excluyentes, se sigue que
Como ser hombre y ser mujer son eventos excluyentes, se sigue que
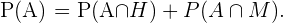
De acuerdo con las reglas de la probabilidad condicional,

Como sabemos 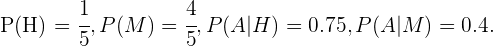
Y sustituyendo estos valores en la expresión anterior, obtenemos que
b Con una mujer con gafas
Del total de la población, sabemos que  corresponde a la proporción de mujeres y
corresponde a la proporción de mujeres y  corresponde a la proporción de los hombres. De esta manera se cumple la condición "el número de mujeres es cuatro veces superior al de hombres".
corresponde a la proporción de los hombres. De esta manera se cumple la condición "el número de mujeres es cuatro veces superior al de hombres".
Observemos que  es la probabilidad de encontrarnos a una mujer con gafas, mientras que
es la probabilidad de encontrarnos a una mujer con gafas, mientras que  es la probabilidad para las mujeres sin gafas. En ambos casos, solamente hemos calculado el cociente de los casos favorables entre los casos totales.
es la probabilidad para las mujeres sin gafas. En ambos casos, solamente hemos calculado el cociente de los casos favorables entre los casos totales.
Sean 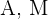 los eventos "tener gafas" y "ser mujer" respectivamente, estamos buscando
los eventos "tener gafas" y "ser mujer" respectivamente, estamos buscando 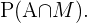
De acuerdo con las reglas de la probabilidad condicional,
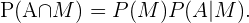
Como sabemos 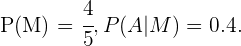 Y sustituyendo estos valores en la expresión anterior, obtenemos que
Y sustituyendo estos valores en la expresión anterior, obtenemos que
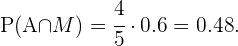
En un centro escolar los alumnos pueden optar por cursar como lengua extranjera inglés o francés. En un determinado curso, el 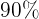 de los alumnos estudia inglés y el resto francés. El
de los alumnos estudia inglés y el resto francés. El  de los que estudian inglés son chicos y de los que estudian francés son chicos el
de los que estudian inglés son chicos y de los que estudian francés son chicos el  . Al elegir un alumno al azar, ¿Cuál es la probabilidad de que sea chica?
. Al elegir un alumno al azar, ¿Cuál es la probabilidad de que sea chica?
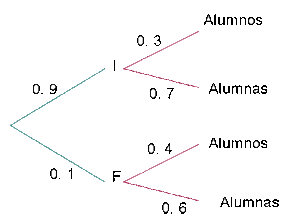
Llamemos 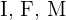 a los eventos "estudiar inglés", "estudiar francés", "ser mujer", respectivamente. Entonces buscamos la probabilidad de elegir una mujer al azar, pero como todas las personas del centro escolar estudian inglés o francés, la probabilidad solicitad puede ser calculada a través de las probabilidades siguientes
a los eventos "estudiar inglés", "estudiar francés", "ser mujer", respectivamente. Entonces buscamos la probabilidad de elegir una mujer al azar, pero como todas las personas del centro escolar estudian inglés o francés, la probabilidad solicitad puede ser calculada a través de las probabilidades siguientes

Para ambas probabilidades podemos hacer,
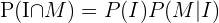
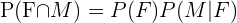
De esta manera podemos utilizar la información proporcionada, pues

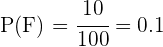
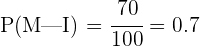

Sustituyendo todos estos valores se obtiene el siguiente cálculo,
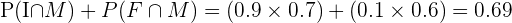
Una caja contiene tres monedas. Una moneda es corriente, otra tiene dos caras y la otra está cargada de modo que la probabilidad de obtener cara es de 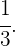 Se selecciona una moneda al azar y se lanza al aire. Hallar la probabilidad de que salga cara
Se selecciona una moneda al azar y se lanza al aire. Hallar la probabilidad de que salga cara
Sea  el evento "elegir la i-ésima moneda", donde
el evento "elegir la i-ésima moneda", donde 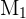 es la moneda corriente,
es la moneda corriente, 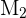 la moneda con dos caras y
la moneda con dos caras y  la moneda cargada. En este contexto, si llamamos
la moneda cargada. En este contexto, si llamamos  al evento "lanzar la moneda y obtener cara", podemos calcular
al evento "lanzar la moneda y obtener cara", podemos calcular  haciendo una intersección con los eventos
haciendo una intersección con los eventos 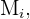 ya que estos son mutuamente excluyentes. Es decir,
ya que estos son mutuamente excluyentes. Es decir,
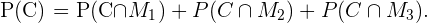
Por la definición de probabilidad condicional, las siguientes igualdades son válidas.

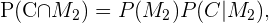
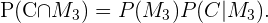
Como la elección de la moneda se realiza al azar, se tiene que 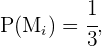 con
con  Luego,
Luego,
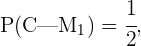
pues la primera moneda es corriente, lo cual quiere decir que cuenta con cara y cruz y puede tomar cualquier valor con igual probabilidad.

pues la esta moneda tiene dos caras, entonces no importa cómo caiga, su valor será cara.
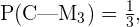
pues la última de las monedas esta cargada para que ésta sea la probabilidad de obtener cara. Así,
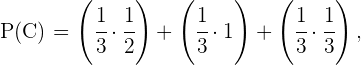

Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3