Halla el número de capicúas de ocho cifras. ¿Cuántos capicúas hay de nueve cifras?
Notemos que para el primer caso el número tiene la forma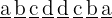
El valor de  no puede ser cero asi que tenemos
no puede ser cero asi que tenemos  posible valores para el primer termino. Para
posible valores para el primer termino. Para  ,
,  y
y  tenemos que ellos pueden ser cualquier numero entre
tenemos que ellos pueden ser cualquier numero entre  y
y  .
.
Finalmente multiplicando concluimos que el número de capicúas de ocho cifras es
Similar al caso anterior el número de  dígitos tiene la forma
dígitos tiene la forma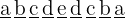
De nuevo el primer dígito no puede ser cero asi que tenemos  posibilidades para la primera posición. Y para los posibles valores que pueden tomar
posibilidades para la primera posición. Y para los posibles valores que pueden tomar  ,
,  ,
,  y
y  tenemos
tenemos  posibilidades. Multiplicando el número de posibles valores para cada una de las posiciones tenemos que hay
posibilidades. Multiplicando el número de posibles valores para cada una de las posiciones tenemos que hay capicúas de nueve cifras.
capicúas de nueve cifras.
Cuatro libros distintos de matemáticas, seis diferentes de física y dos diferentes de química se colocan en un estante. De cuántas formas distintas es posible ordenarlos si:
1Los libros de cada asignatura deben estar todos juntos. Dado que los libros de cada asignatura van juntos y a su vez cada libro es diferente entonces podemos calcular primero por separado el número de permutaciones en matemáticas, física y química. Respectivamente tenemos que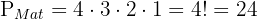

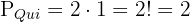 Dado que tenemos tres materias distintas primero podría venir un libro de química o matemáticas y luego uno de física o un física primero y luego uno de química. El número total de permutaciones de este tipo es
Dado que tenemos tres materias distintas primero podría venir un libro de química o matemáticas y luego uno de física o un física primero y luego uno de química. El número total de permutaciones de este tipo es  . Finalmente multiplicando tenemos que el número de formas de colocar los libro es
. Finalmente multiplicando tenemos que el número de formas de colocar los libro es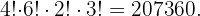
2 Solamente los libros de matemáticas deben estar juntos.Ahora solo tenemos dos clases, los libro de matemáticas y el resto. En total el resto son  libros así el número total de permutaciones para el resto de los libro es
libros así el número total de permutaciones para el resto de los libro es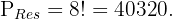 Ya que bien puede venir primero un libro de matemáticas, química o física debemos multiplicar por
Ya que bien puede venir primero un libro de matemáticas, química o física debemos multiplicar por  al producto de
al producto de  y
y 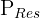 para obtener el resultado final,
para obtener el resultado final,
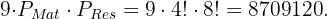
Una persona tiene cinco monedas de distintos valores. ¿Cuántas sumas diferentes de dinero puede formar con las cinco monedas?
Podemos contar primero cuantas sumas de dinero tendrá si solo usa una moneda, luego dos, luego tres, luego cuatro y finalmente cinco. Esto lo hacemos tomando el número de combinaciones de uno entre cinco, dos entre cinco, tres entre cinco y asi sucesivamente. Si al final sumamos obtenemos nuestro resultado,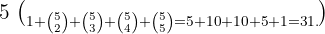
Se ordenan en una fila 5 bolas rojas, 2 bolas blancas y 3 bolas azules. Si las bolas de igual color no se distinguen entre sí, ¿de cuántas formas posibles pueden ordenarse?
En este caso tenemos un problema de permutación con repetición ya que las bolas de igual color no se distinguen. Utilizando el principio multiplicativo obtenemos una formula para resolver esto, lo que nos da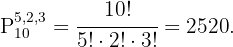
Resolver las ecuaciones combinatorias:

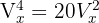
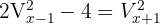

Recordemos que  y
y 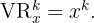


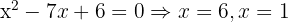 Tomamos la solución
Tomamos la solución 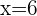 .
.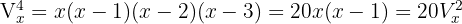

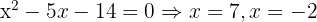 Tomamos la solución
Tomamos la solución  .
.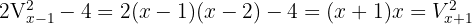
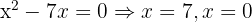 Tomamos la solución
Tomamos la solución  .
.
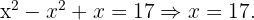
Resolver las ecuaciones combinatorias:
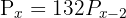
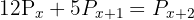
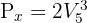
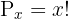 y
y 
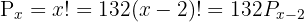

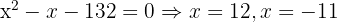 Tomamos la solución
Tomamos la solución 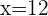 .
.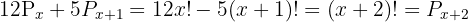
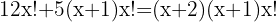
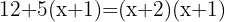
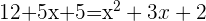
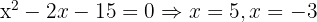 Tomamos la solución
Tomamos la solución  .
.

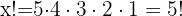 Entonces
Entonces  .
.Resolver las ecuaciones combinatorias:
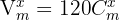


Recordemos que 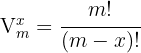 y
y 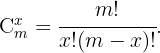
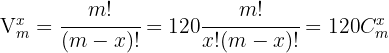

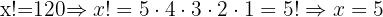
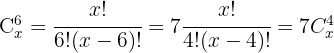
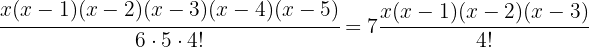

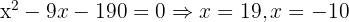 Tomamos la solución
Tomamos la solución  .
.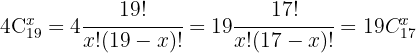
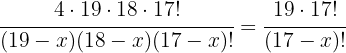

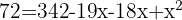
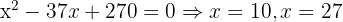 Tomamos la solución
Tomamos la solución 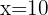 .
.  no es solución porque el número de orden en las combinaciones es menor que el número de elementos.
no es solución porque el número de orden en las combinaciones es menor que el número de elementos.Resolver las ecuaciones combinatorias:
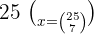
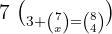
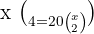
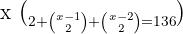
1
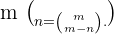 Entonces,
Entonces, 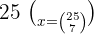 implica que
implica que 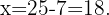
 Entonces,
Entonces, 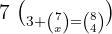 implica que
implica que 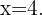
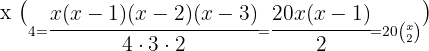
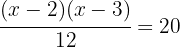
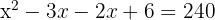
 Tomamos la solución
Tomamos la solución 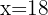 .
.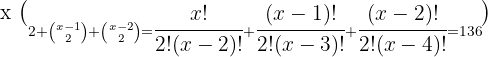
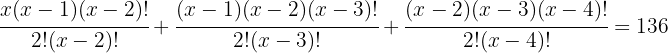
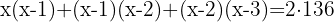
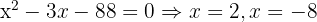 Tomamos la solución
Tomamos la solución  .
.Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3