
Repaso sobre permutaciones
El número de maneras distintas en que se pueden ordenar los elementos de un conjunto es llamado una permutación. En una permutación importa el orden de los grupos.
Si no se repiten los elementos en el conjunto, el total de maneras en que se pueden colocar m elementos en grupos de tamaño n viene dado por la fórmula
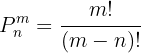
Si en dado caso m=n, para calcular el total de permutaciones se utiliza la siguiente fórmula:
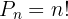
Si se repiten los elementos en el conjunto, esto es, el primer elemento se repite  veces, el segundo
veces, el segundo 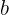 veces y así sucesivamente, siendo
veces y así sucesivamente, siendo 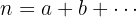 , el número de permutaciones tomando en cuenta los elementos repetidos se obtiene con la fórmula
, el número de permutaciones tomando en cuenta los elementos repetidos se obtiene con la fórmula
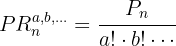
Ejercicios de permutaciones
¿Cuántos números de 5 cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5?
1 Establecemos las condiciones del ejercicio:
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos. El enunciado nos pide que las cifras sean diferentes
2 Se trata de una Permutación por lo que utilizamos la fórmula:
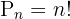
3 Sustituimos y resolvemos:
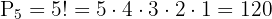
¿De cuántas formas distintas pueden sentarse ocho personas en una fila de butacas?
1 Establecemos las condiciones del ejercicio:
Sí entran todos los elementos. Tienen que sentarse 8 personas
Sí importa el orden
No se repiten los elementos. Una persona no se puede repetir
2 Se trata de una Permutación por lo que utilizamos la fórmula:
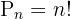
3 Sustituimos y resolvemos:
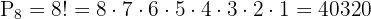
¿De cuántas formas distintas pueden sentarse ocho personas alrededor de una mesa redonda?
1 Establecemos las condiciones del ejercicio:
Sí entran todos los elementos. Tienen que sentarse 8 personas
Al ser un arreglo circular debemos eliminar las repeticiones circulares
No se repiten los elementos. Una persona no se puede repetir
2 Se trata de una Combinación por lo que utilizamos la fórmula:
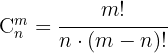

3 Sustituimos y resolvemos:
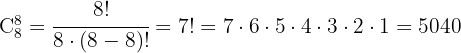
Con las cifras 2, 2, 2, 3, 3, 3, 3, 4, 4; ¿cuántos números de nueve cifras se pueden formar?
1 Tenemos 3 elementos a, b, c, que se repiten:
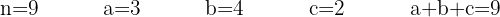
2 Se trata de una permutación con varios elementos que se repiten por lo que usamos la fórmula:
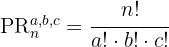
3 Sustituimos en la fórmula y resolvemos:
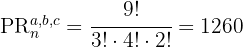
Con las letras de la palabra libro. ¿Cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
1 La palabra empieza por i u o seguida de las 4 letras restantes tomadas de 4 en 4.
2 Establecemos las condiciones:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
3 Al tener 2 vocales con las que puede iniciar podemos calcular el resultado con:
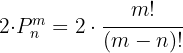
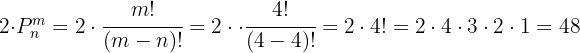
¿Cuántos números de cinco cifras distintas se pueden formar con las cifras impares? ¿Cuántos de ellos son mayores de 70.000?
1 Establecemos las condiciones:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
2 Para encontrar los números de cinco cifras usando los dígitos impares (1,3,5,7,9) usamos la siguiente fórmula:
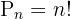
Sustituimos y resolvemos:
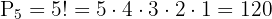
Para encontrar los números que sean mayores a 70000 consideramos aquellos que empiecen con 7 u 8
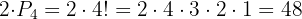
En el palo de señales de un barco se pueden izar tres banderas rojas, dos azules y cuatro verdes. ¿Cuántas señales distintas pueden indicarse con la colocación de las nueve banderas?
1 Tenemos 3 elementos a, b, c, que se repiten:
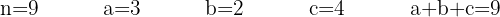
2 Se trata de una permutación con varios elementos que se repiten por lo que usamos la fórmula:
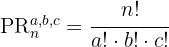
3 Sustituimos en la fórmula y resolvemos:
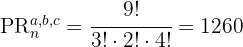
¿De cuántas formas pueden colocarse los 11 jugadores de un equipo de fútbol teniendo en cuenta que el portero no puede ocupar otra posición distinta que la portería?
1 Establecemos las condiciones del ejercicio:
Disponemos de 10 jugadores que pueden ocupar 10 posiciones distintas.
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
2 Se trata de una Permutación por lo que utilizamos la fórmula:
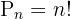
3 Sustituimos y resolvemos:
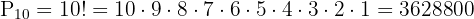
Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?
1 Consideramos las dos personas que deben ir juntas como una sola lo cual se logra de 2! maneras. Ahora hay siete personas para sentar alrededor de la mesa y se cumple que:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
2 Podemos resolver el ejercicio con:
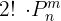
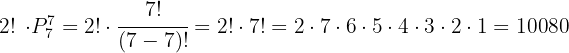
Cuatro libros distintos de matemáticas, seis diferentes de física y dos diferentes de química se colocan en un estante. De cuántas formas distintas es posible ordenarlos si:
1 Los libros de cada asignatura deben estar todos juntos.
2 Solamente los libros de matemáticas deben estar juntos.
1 Los libros de cada asignatura deben estar todos juntos.
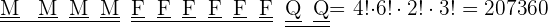
2Solamente los libros de matemáticas deben estar juntos.
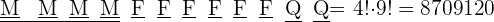
Se ordenan en una fila 5 bolas rojas, 2 bolas blancas y 3 bolas azules.
Si las bolas de igual color no se distinguen entre sí. ¿De cuántas formas posibles pueden ordenarse?
1 Tenemos 3 elementos a, b, c, que se repiten:
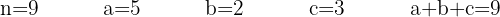
2 Se trata de una permutación con varios elementos que se repiten por lo que usamos la fórmula:
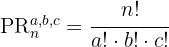
3 Sustituimos en la fórmula y resolvemos:
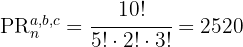
Resolver las ecuaciones
1 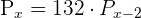
2 
3 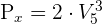
1 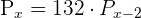
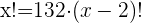
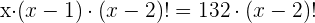
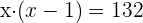
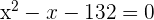

Descartamos la solución negativa por lo que 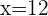
2 

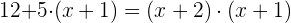
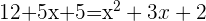


Descartamos la solución negativa por lo que 
3 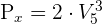
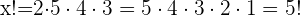
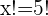

Si tienes alguna duda, en Superprof te ofrecemos el mejor profesor de mates. ¿Prefieres un profesor de matematicas online? También podrás encontrarlo en nuestra página.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3