Capítulos
¡Bienvenidos a nuestra página dedicada a problemas de permutaciones, variaciones y combinaciones! Hemos diseñado esta página para proporcionarte un aprendizaje dinámico y eficiente en el estudio de estas importantes ramas de la probabilidad.
Recordemos que, una permutación es una disposición ordenada de objetos tomados de un conjunto, en la que el orden importa. Se utiliza cuando se seleccionan todos los elementos de un conjunto para formar una secuencia.
Una variación es similar a una permutación, pero en este caso no se utilizan todos los elementos del conjunto. Se refiere a una disposición ordenada de r elementos tomados de un conjunto de n elementos, donde el orden sigue siendo importante.
Una combinación es una selección no ordenada de elementos tomados de un conjunto, en la que el orden no importa. Se utiliza cuando se eligen elementos de un conjunto sin preocuparse por el orden en que se seleccionan.
A continuación presentamos una gran variedad de ejercicios con soluciones deplegables sobre estos tres importantes conceptos. ¡Échales un vistazo y perfecciona tus habilidades!

Permutaciones
¿De cuántas formas distintas pueden sentarse ocho personas en una fila de butacas?
Sí entran todos los elementos. En la fila se está considerando que se sienten las  personas.
personas.
Sí importa el orden. Si los ordenas diferentes, eso contaría como otra forma.
No se repiten los elementos. Una persona no se puede repetir.
Por las características, se trata de una permutación.

¿Cuántos números de  cifras diferentes se puede formar con los dígitos:
cifras diferentes se puede formar con los dígitos:  ?
?
Notemos que en la pregunta se mencionan  cifras diferentes.
cifras diferentes.


No entran todos los elementos. De  dígitos entran sólo
dígitos entran sólo 
Sí importa el orden. Son números distintos el 
No se repiten los elementos. El enunciado nos pide que las cifras sean diferentes
Por las características, se trata de una variación

¿De cuántas formas distintas pueden sentarse ocho personas alrededor de una mesa redonda?
En este caso nos interesa calcular de cuantas formas se pueden acomodar  personas en un arreglo circular, por lo que, debemos recurrir a las permutaciones circulares
personas en un arreglo circular, por lo que, debemos recurrir a las permutaciones circulares

¿Cuántas quinielas de futbol han de rellenarse para asegurarse el acierto de los  resultados?
resultados?
En cada uno de los  partidos, se puede elegir apostar por que el equipo local gane, empate o pierda, por lo que
partidos, se puede elegir apostar por que el equipo local gane, empate o pierda, por lo que
 m < n
m < n
Sí entran todos los elementos. En este caso el número de orden es mayor que el número de elementos
Sí importa el orden.
Sí se repiten los elementos.
Por las características, se trata de una variación

Con las cifras  y
y  , ¿cuántos números de cinco cifras pueden formarse? ¿Cuántos son pares?
, ¿cuántos números de cinco cifras pueden formarse? ¿Cuántos son pares?
1 Números de  cifras
cifras
Sí entran todos los elementos: 
Sí importa el orden
Sí se repiten los elementos
Por las características, se trata de una variación con repetición

2 Números de
 cifras pares
cifras pares Si el número es par tan sólo puede terminar en  .
.

Con las cifras  ¿cuántos números de nueve cifras se pueden formar?
¿cuántos números de nueve cifras se pueden formar?

Sí entran todos los elementos
Sí importa el orden
Sí se repiten los elementos
Por las características, se trata de una permutación con repetición

Con las letras de la palabra libro, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
La palabra empieza por i u o seguida de las  letras restantes tomadas de
letras restantes tomadas de  en
en  .
.
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de permutaciones


Para la primer letra hay
 maneras de hacerlo y para el resto hay
maneras de hacerlo y para el resto hay  , pues se trata de ordenar las letras l, b, r, y la que no usé al principio. Entonces las formas totales es igual a
, pues se trata de ordenar las letras l, b, r, y la que no usé al principio. Entonces las formas totales es igual a
¿Cuántos números de cinco cifras distintas se pueden formar con las cifras impares? ¿Cuántos de ellos son mayores de 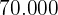 ?
?
1 Números de cinco cifras distintas
La cifras impares:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de una permutación

2 Mayores a

Si es impar sólo puede empezar por 7 u 8



En el palo de señales de un barco se pueden izar tres banderas rojas, dos azules y cuatro verdes. ¿Cuántas señales distintas pueden indicarse con la colocación de las nueve banderas?
Sí entran todos los elementos.
Sí importa el orden
Sí se repiten los elementos
Por las características, se trata de una permutación con repetición

Una mesa presidencial está formada por ocho personas, ¿de cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?
Primero tengo que considerar cuántas maneras hay de acomodar el espacio para el presidente y el secretario. Este espacio para dos personas puede ser a partir del primer lugar, del segundo, del tercero hasta el séptimo, en el cual el presidente y el secretario ocupan los últimos dos lugares. En total hay  formas de elegir este espacio.
formas de elegir este espacio.
Se forman dos grupos el primero de  personas (presidente y secretario) y el segundo de
personas (presidente y secretario) y el segundo de  personas, en los dos se cumple que:
personas, en los dos se cumple que:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de permutaciones.

Se ordenan en una fila  bolas rojas,
bolas rojas,  bolas blancas y
bolas blancas y  bolas azules. Si las bolas de igual color no se distinguen entre sí, ¿de cuántas formas posibles pueden ordenarse?
bolas azules. Si las bolas de igual color no se distinguen entre sí, ¿de cuántas formas posibles pueden ordenarse?
Sí entran todos los elementos
Sí importa el orden
Sí se repiten los elementos
Por las características, se trata de una permutación con repetición.

Cuatro libros distintos de matemáticas, seis diferentes de física y dos diferentes de química se colocan en un estante. De cuántas formas distintas es posible ordenarlos si:
1Los libros de cada asignatura deben estar todos juntos.
2Solamente los libros de matemáticas deben estar juntos.
1 Los libros de cada asignatura deben estar todos juntos.
Orden de las materias

Primero se tiene que elegir el orden que llevarán las materias. Por ejemplo: primero los libros de matemáticas, luego los de química, y finalmente los de física. Son 3 materias, donde
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de una permutación.
Hay 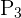 de elegir el acomodo de las materias.
de elegir el acomodo de las materias.
¿Necesitas repasar conceptos con un profesor de matematicas?
Orden de los libros por sección
Ya que se eligió ese acomo, calculamos las maneras de acomodar los libros de cada materia en el espacio que le correspondería.
De nuevo
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de permutaciones.
Hay  formas de acomodar los libros de matemáticas en el espacio que le corresponde,
formas de acomodar los libros de matemáticas en el espacio que le corresponde,  de acomodar los libros de física y
de acomodar los libros de física y  de acomodar los libros de química.
de acomodar los libros de química.
Finalmente, las formas totales de acomodo son:

2 Solamente los libros de matemáticas deben estar juntos.
Orden de la sección de matemáticas

Primero tengo que considerar cuántas maneras hay de acomodar el espacio para los 4 libros de matemáticas en el estante.
El espacio para los libros de matemáticas puede comenzar desde el primer espacio, desde el segundo, tercero, ... hasta el noveno, pues de este modo los  libros de matemáticas quedarían al final, como se muestra a continuación
libros de matemáticas quedarían al final, como se muestra a continuación

Entonces en total hay  formas para elegir la posición en la que irá el apartado de libros de matemáticas.
formas para elegir la posición en la que irá el apartado de libros de matemáticas.
Orden de los libros del espacio asignado
Ya teniendo el apartado elegido, hay
 maneras de acomodar los libros de matemáticas en ese espacio.
maneras de acomodar los libros de matemáticas en ese espacio. Quedan 8 lugares vacíos, para acomodar el resto de libros, sin ninguna restricción, donde
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de una permutación. Hay
 maneras de ordenar el resto de libros.
maneras de ordenar el resto de libros. En total, las maneras de ordenar los libros en el estante donde los libros de matemáticas estén juntos son:

¿Cuántos órdenes de bateo diferentes son posibles para un equipo de béisbol de  jugadores?
jugadores?
Como cada jugador de béisbol puede tomar un turno para batear, sí importa el orden y no se permiten repeticiones, entonces se trata de una permutación. Así, hay

Una clase de matemáticas consiste de  mujeres y
mujeres y  hombres. El profesor de la asignatura decide hacer un examen en el cual todos los estudiantes serán rankeados de acuerdo a su desempeño en el examen. Si asumimos que no dos estudiantes obtienen la misma calificación:
hombres. El profesor de la asignatura decide hacer un examen en el cual todos los estudiantes serán rankeados de acuerdo a su desempeño en el examen. Si asumimos que no dos estudiantes obtienen la misma calificación:
1¿Cuántos rankings diferentes son posibles?
2Si las mujeres son rankeadas entre ellas mismas y los hombres entre ellos mismos, ¿cuántos rankings diferentes son posibles?
1 Dado que cada ranking corresponde a un arreglo ordenado particular de  personas, en el cual sí importa el orden y no se permiten repeticiones, entonces la respuesta a esta parte es
personas, en el cual sí importa el orden y no se permiten repeticiones, entonces la respuesta a esta parte es

2 Ahora consideramos a las mujeres y a los hombres por separado. Dado que hay  posibles rankings para las mujeres y
posibles rankings para las mujeres y  posibles rankings para los hombres, se sigue que hay
posibles rankings para los hombres, se sigue que hay

Un torneo de ajedrez tiene como participantes a  competidores de los cuales
competidores de los cuales  son de Estados Unidos,
son de Estados Unidos,  son de Rusia,
son de Rusia,  son de la India y
son de la India y  es de España. Si al finalizar el torneo, la organización solo muestra las nacionalidades de los jugadores en la posición en la que finalizaron en el torneo, ¿cuántos rankings son posibles?
es de España. Si al finalizar el torneo, la organización solo muestra las nacionalidades de los jugadores en la posición en la que finalizaron en el torneo, ¿cuántos rankings son posibles?
Como sabemos, si enuméramos a los jugadores del  , entonces tendríamos un total de
, entonces tendríamos un total de  rankings distintos posibles. Ahora, como lo único relevante es la nacionalidad y no el competidor por si solo, debemos dividir entre las posibles permutaciones que puede tener cada país.
rankings distintos posibles. Ahora, como lo único relevante es la nacionalidad y no el competidor por si solo, debemos dividir entre las posibles permutaciones que puede tener cada país.
Como Estados Unidos tiene  competidores, entonces tiene
competidores, entonces tiene  posibles permutaciones de sus
posibles permutaciones de sus  jugadores. Similarmente, Rusia tiene
jugadores. Similarmente, Rusia tiene  , la India
, la India  y finalmente, España
y finalmente, España  . Por lo tanto, los posibles rankings están dados por
. Por lo tanto, los posibles rankings están dados por

Variaciones
¿Cuántos números de tres cifras se puede formar con los dígitos:  ?
?
1 Primer dígito

Tenemos que separar el número en dos bloques:

El primer bloque, de un número, lo puede ocupar sólo uno de  dígitos porque un número no comienza por cero (excepto los de las matriculas, los de la lotería y otros casos particulares),
dígitos porque un número no comienza por cero (excepto los de las matriculas, los de la lotería y otros casos particulares),

2 Segundo y tercer dígito
El segundo bloque, de dos números, lo puede ocupar cualquier dígito.

En ambos casos
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
Por las características, se tratan de variaciones
Las maneras de llenar el primer bloque multiplicado por las maneras de elegir el segundo nos da el total de números de  dígitos
dígitos

Con el (punto, raya) del sistema Morse, ¿cuántas señales distintas se pueden enviar, usando como máximo cuatro pulsaciones?
Con máximo  pulsaciones, hay
pulsaciones, hay  casos a considerar: señales con
casos a considerar: señales con  , con
, con  , con
, con  o con
o con  pulsaciones.
pulsaciones.
No entran todos los elementos en el caso de señales con  pulsación y sí entran en lo otros
pulsación y sí entran en lo otros
Sí importa el orden
Sí se repiten los elementos
Por las características, se trata de una variación con repetición

¿De cuántas formas diferentes se pueden cubrir los puestos de presidente, vicepresidente y tesorero de un club de fútbol sabiendo que hay  posibles candidatos?
posibles candidatos?
No entran todos los elementos
Sí importa el orden
No se repiten los elementos
Por las características, se trata de una variación.

Halla el número de capicúas de ocho cifras. ¿Cuántos capicúas hay de nueve cifras?
Números capicúas son números con la propiedad de que se leen igual de izquierda a derecha que de derecha a izquierda. 1 Capicúas de  dígitos
dígitos

Como las cifras a partir de la quinta vienen en función de la
 primeras, el número de capicúas de ocho cifras coincide con el de números de
primeras, el número de capicúas de ocho cifras coincide con el de números de  cifras. Entonces tengo que ver de cuántas maneras puedo elegir valores para a, b, c y d, con
cifras. Entonces tengo que ver de cuántas maneras puedo elegir valores para a, b, c y d, con  .
. Para ello puedo obtener los números de  cifras y restar las que comiencen con
cifras y restar las que comiencen con  .
.

No entran todos los elementos. Tengo de elementos a las  cifras y me interesa asignar valores a
cifras y me interesa asignar valores a  letras\espacios.
letras\espacios.
Sí importa el orden
Sí se repiten los elementos
Por las características, se trata de una variación con repetición.

2 Capicúas de
 dígitos
dígitosAnálogamente al caso anterior,

Considero lo números de
 cifras.
cifras. 
Al total le resto los números que inician con  .
.
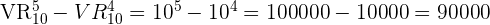
En un mundial de fútbol participan  selecciones nacionales de todo el mundo. Si todos los países tienen las mismas posibilidades de ganar el mundial, ¿cuántos posibles arreglos de campeón y subcampeón podemos tener?
selecciones nacionales de todo el mundo. Si todos los países tienen las mismas posibilidades de ganar el mundial, ¿cuántos posibles arreglos de campeón y subcampeón podemos tener?
No entran todos los elementos
Sí importa el orden, no es lo mismo que Brasil sea el campeón y Alemania subcampeón, a que Alemania sea campeón y Brasil sea subcampeón.
No se repiten los elementos
Por las características, se trata de una variación.

Combinaciones
¿De cuántas formas pueden mezclarse los siete colores del arco iris tomándolos de tres en tres?
No entran todos los elementos. Pues de los  se considerarán grupos de
se considerarán grupos de  .
.
No importa el orden. Es una mezcla, así que rojo, azul y amarillo dan el mismo color que amarillo, azul y rojo.
No se repiten los elementos. Como se toman  colores del arcoíris se entiende que tienen que ser diferentes.
colores del arcoíris se entiende que tienen que ser diferentes.
Por las características, se trata de una combinación

En una clase de  alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
No entran todos los elementos. El comité es de  personas únicamente.
personas únicamente.
No importa el orden: Juan, Ana y Betti, forman el mismo comité que Betti, Juan y Ana.
No se repiten los elementos. El comité no puede estar formado por Betti, Betti y Betti. Una persona no se puede repetir.
Por las características, se trata de una combinación

¿Cuántas apuestas de Lotería Primitiva de una columna han de rellenarse para asegurarse el acierto de los seis resultados, de  ?
?
Esta loteria consiste en elegir  números de
números de  . Al llevar a cabo la lotería, se obtienen aleatoriamente
. Al llevar a cabo la lotería, se obtienen aleatoriamente  números. Si esos números fueron elegidos por alguien que apostó, se convierte en ganador.
números. Si esos números fueron elegidos por alguien que apostó, se convierte en ganador.
No entran todos los elementos. Se toma en cuenta  elementos de los
elementos de los  .
.
No importa el orden.
No se repiten los elementos.
Por las características, se trata de una combinación

En una bodega hay en un cinco tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?
No entran todos los elementos. Sólo elije 4
No importa el orden. Da igual que elija  botellas de anís y
botellas de anís y  de ron, que
de ron, que  de ron y
de ron y  de anís
de anís
Sí se repiten los elementos. Puede elegir más de una botella del mismo tipo
Por las características, se trata de una combinación con repetición

¿Cuántas diagonales tiene un pentágono y cuántos triángulos se puede informar con sus vértices?
Determinaremos las rectas que se pueden trazar con  vértices de los
vértices de los  disponibles (y triángulos con
disponibles (y triángulos con  vértices).
vértices).
No entran todos los elementos
No importa el orden
No se repiten los elementos
Por las características, se trata de combinaciones
Son  , a las que tenemos que restar los lados que forman
, a las que tenemos que restar los lados que forman  rectas que no son diagonales.
rectas que no son diagonales.
 diagonales
diagonales
 triángulos
triángulos
Un grupo, compuesto por cinco hombres y siete mujeres, forma un comité de  hombres y
hombres y  mujeres. De cuántas formas puede formarse, si:
mujeres. De cuántas formas puede formarse, si:
1Puede pertenecer a él cualquier hombre o mujer.
2Una mujer determinada debe pertenecer al comité.
3Dos hombres determinados no pueden estar en el comité.
No entran todos los elementos
No importa el orden
No se repiten los elementos
Por las características, trabajaremos con combinaciones
1 Puede pertenecer a él cualquier hombre o mujer.

2 Una mujer determinada debe pertenecer al comité.

3 Dos hombres determinados no pueden estar en el comité.

Con nueve alumnos de una clase se desea formar tres equipos de tres alumnos cada uno. ¿De cuántas maneras puede hacerse?
Para este problema veremos de cuántas maneras podemos armar al primer equipo y luego lo multiplicaremos por las maneras de formar al segundo por las maneras de formar al tercero.
No entran todos los elementos. Pues se eligen a  personas de las que quedan disponibles.
personas de las que quedan disponibles.
No importa el orden.
No se repiten los elementos
Por las características, se trata de una combinación.

Una persona tiene cinco monedas de distintos valores. ¿Cuántas sumas diferentes de dinero puede formar con las cinco monedas?
Consideramos las sumas formadas por  moneda,
moneda,  monedas,
monedas,  monedas,
monedas,  monedas o
monedas o  monedas
monedas
No entran todos los elementos (Sí, en el caso de que se usen las  monedas)
monedas)
No importa el orden
No se repiten los elementos
Por las características, se trata de combinaciones.

Una compañía rifa  televisiones iguales entre sus
televisiones iguales entre sus  trabajadores. ¿De cuántas formas se puede elegir a los ganadores?
trabajadores. ¿De cuántas formas se puede elegir a los ganadores?
Como las televisiones son iguales y solo nos interesa en sacar a los ganadores, entonces el orden no importa, por lo tanto estamos ante una combinación. Debemos sacar a  personas de entre
personas de entre  que serán los ganadores. Así, tenemos que el número de formas es
que serán los ganadores. Así, tenemos que el número de formas es

.
¿Cuántos subconjuntos hay en un conjunto de  elementos?
elementos?
Por definición, hay  subconjuntos de tamaño
subconjuntos de tamaño  en un conjunto que contiene
en un conjunto que contiene  elementos. Por lo tanto, buscamos subconjuntos de tamaño "cero" (el vacío), tamaño
elementos. Por lo tanto, buscamos subconjuntos de tamaño "cero" (el vacío), tamaño  y
y  . Así, la respuesta que buscamos es
. Así, la respuesta que buscamos es

Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3