En este artículo presentamos diversos ejercicios de probabilidad los cuales serán resueltos usando el conocido Teorema de Bayes. Pero antes de pasar a los ejercicios, recordemos lo que nos dice el Teorema de Bayes.
Teorema de Bayes: Sean  eventos mutuamente excluyentes y cuya unión es el espacio muestral
eventos mutuamente excluyentes y cuya unión es el espacio muestral  , esto es,
, esto es,
Si  es otro evento, entonces
es otro evento, entonces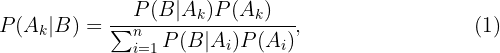
donde 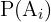 representa la probabilidad del evento
representa la probabilidad del evento  denominada probabilidad a priori,
denominada probabilidad a priori, 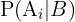 representa la probabilidad del evento
representa la probabilidad del evento  dado el evento
dado el evento  también conocida como probabilidad a posteriori, y
también conocida como probabilidad a posteriori, y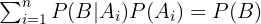 es la probabilidad total del evento
es la probabilidad total del evento  La ecuación (1) es conocida como la fórmula de Bayes.
La ecuación (1) es conocida como la fórmula de Bayes.
Ejemplos resueltos
Se tienen dos urnas. La urna I contiene 4 sobres blancos y 6 sobres negros. La urna II contiene 4 sobres blancos y 2 sobres negros. Si se saca un sobre al azar de una de las 2 urnas y se sabe que el sobre es de color negro, ¿cuál es la probabilidad de que el sobre haya salido de la urna I?
Considere los siguientes eventos con sus respectivas probabilidades:
 "Se elige la urna I"
"Se elige la urna I" 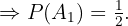
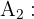 "Se elige la urna II"
"Se elige la urna II" 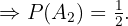
También considere el evento 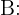 "Se saca un sobre negro".
"Se saca un sobre negro".
Las hipótesis del problema nos indican que:
La probabilidad de sacar un sobre negro de la urna I es 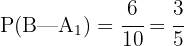 ya que en la urna tenemos 10 sobres en total de los cuales 6 son negros.
ya que en la urna tenemos 10 sobres en total de los cuales 6 son negros.
La probabilidad de sacar un sobre negro de la urna II es 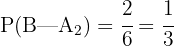 ya que en la urna tenemos 6 sobres en total de los cuales 2 son negros.
ya que en la urna tenemos 6 sobres en total de los cuales 2 son negros.
Por lo tanto, estamos interesados en conocer 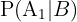 , es decir, la probabilidad de que el sobre negro haya salido de la urna I.
, es decir, la probabilidad de que el sobre negro haya salido de la urna I.
Siguiendo la fórmula de Bayes tenemos que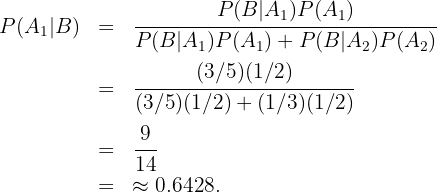
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
Considere los siguientes eventos con sus respectivas probabilidades:
 "La moneda cae cara"
"La moneda cae cara"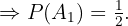
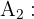 "La moneda cae cruz"
"La moneda cae cruz"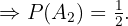
Además, considere el evento 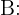 " El hombre dice que la moneda cayó cara".
" El hombre dice que la moneda cayó cara".
Las hipótesis del problema nos indican que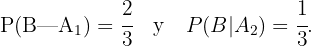
Estamos interesados en conocer 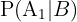 , es decir, la probabilidad de que la moneda haya caído cara dado que el hombre dijo que cayó cara. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que la moneda haya caído cara dado que el hombre dijo que cayó cara. Siguiendo la fórmula de Bayes tenemos que

Si eres más de aprender desde casa, igual te interesan nuestras clases matematicas online.
En un examen de opción múltiple, la probabilidad de saber la respuesta es  . Si hay
. Si hay  opciones, la probabilidad de atinarle a la respuesta correcta sin saber es de
opciones, la probabilidad de atinarle a la respuesta correcta sin saber es de 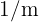 . Dado que un estudiante obtuvo una respuesta correcta, ¿cuál es la probabilidad de que en realidad sabe la respuesta?
. Dado que un estudiante obtuvo una respuesta correcta, ¿cuál es la probabilidad de que en realidad sabe la respuesta?
Considere los siguientes eventos con sus respectivas probabilidades:
 "El estudiante sabe la respuesta"
"El estudiante sabe la respuesta" 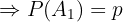
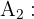 "El estudiante no sabe la respuesta"
"El estudiante no sabe la respuesta" 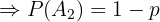
Además, considere el evento 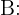 "El estudiante contestó correctamente".
"El estudiante contestó correctamente".
Las hipótesis del problema nos indican que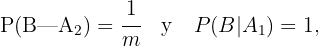
donde en la segunda probabilidad asumimos que, dado que el estudiante sabe la respuesta, entonces contestará correctamente.
Estamos interesados en conocer 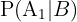 , es decir, la probabilidad de que el estudiante sepa la respuesta dado que contestó correctamente. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que el estudiante sepa la respuesta dado que contestó correctamente. Siguiendo la fórmula de Bayes tenemos que
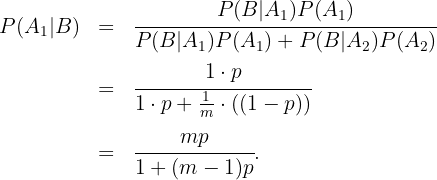
Por ejemplo, si 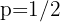 y
y 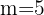 , entonces tenemos que
, entonces tenemos que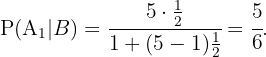
Una pareja tiene dos hijos y uno de ellos es de hecho mujer y se llama Cristina. Si la proporción de mujeres que tienen el nombre "Cristina" en el mundo es 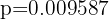 , ¿cuál es la probabilidad de que la pareja tenga dos hijas?
, ¿cuál es la probabilidad de que la pareja tenga dos hijas?
Considere los siguientes eventos con sus respectivas probabilidades:
 "La pareja tiene dos hijas"
"La pareja tiene dos hijas"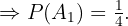
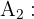 "La pareja tiene una hija y un hijo"
"La pareja tiene una hija y un hijo"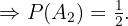
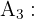 "La pareja tiene dos hijos"
"La pareja tiene dos hijos"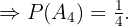
Las probalilidades de arriba se pueden obtener directamente al asumir que las 4 posibilidades (2 hijas, 1 hija y 1 hijo, 1 hijo y 1 hija, y 2 hijos) tienen la probabilidad de 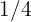 y donde las dos posibilidades de en medio están incluidas en el evento
y donde las dos posibilidades de en medio están incluidas en el evento 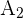 , lo cual justifica su probabilidad de
, lo cual justifica su probabilidad de 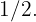
Ahora, considere el evento 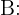 "Una es hija y se llama Cristina". Las hipótesis del problema nos indican que
"Una es hija y se llama Cristina". Las hipótesis del problema nos indican que 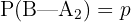
y obviamente que 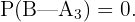 De igual manera obtenemos que
De igual manera obtenemos que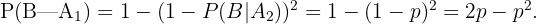
Estamos interesados en conocer 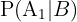 , es decir, la probabilidad de que la pareja tenga 2 hijas sabiendo a priori que una de ellas se llama Cristina. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que la pareja tenga 2 hijas sabiendo a priori que una de ellas se llama Cristina. Siguiendo la fórmula de Bayes tenemos que
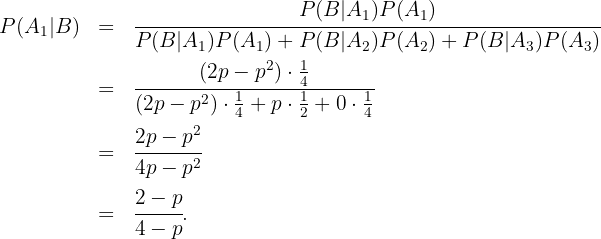
Sustituyendo 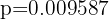 , obtenemos que
, obtenemos que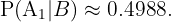
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3