
El Teorema de Bayes
El Teorema de Bayes es uno de los resultados más conocidos y útiles en el área de la probabilidad y estadística, y en particular en el estudio de la probabilidad condicional. Básicamente, el Teorema de Bayes nos dice cómo calcular la probabilidad de un suceso teniendo información a priori sobre dicho suceso.
Este teorema es una herramienta altamente usada por su simpleza y su rápida aplicación en distintas áreas del conocimiento, por ejemplo en medicina, biología, tecnología, negocios, o en cualquier área en la que se necesite tener una certeza sobre algún suceso dada información de antemano. Además, es común utilizar dicha herramienta consecutivamente para obtener una mayor certeza si el problema así lo requiere.
A continuación enunciaremos dicho teorema y resolveremos algunos ejercicios para ilustrar mejor este importante resultado.
Teorema de Bayes: Sean  eventos mutuamente excluyentes y cuya unión es el espacio muestral
eventos mutuamente excluyentes y cuya unión es el espacio muestral  , esto es,
, esto es,

Si  es otro evento, entonces
es otro evento, entonces
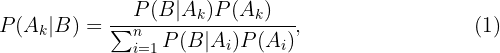
donde
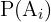 representa la probabilidad del evento
representa la probabilidad del evento  denominada probabilidad a priori,
denominada probabilidad a priori,
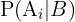 representa la probabilidad del evento
representa la probabilidad del evento  dado el evento
dado el evento  también conocida como probabilidad a posteriori, y
también conocida como probabilidad a posteriori, y
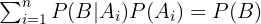 es la probabilidad total del evento
es la probabilidad total del evento  La ecuación (1) es conocida como la fórmula de Bayes.
La ecuación (1) es conocida como la fórmula de Bayes.
Ejemplos resueltos del Teorema de Bayes
Se tienen dos cajas, la primera contiene 3 bolas rojas y 2 azules mientras que la segunda contiene 2 rojas y 8 azules. Se lanza una moneda, si se obtiene cara se saca una bola de la primera caja y si se obtiene sello se saca una bola de la segunda. Si se sabe que la bola obtenida es azul, ¿cuál es la probabilidad de que provenga de la primera caja?
Considere los siguientes eventos y sus probabilidades:
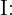 "Se saca una bola de la caja I"
"Se saca una bola de la caja I"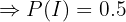
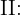 "Se saca una bola de la caja II"
"Se saca una bola de la caja II"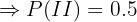
Además, considere el evento
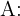 "Sale una bola azul". El ejercicio nos da también las siguientes probabilidades:
"Sale una bola azul". El ejercicio nos da también las siguientes probabilidades: 
Estamos interesados en conocer 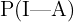 , es decir, la probabilidad de que la bola se extraiga de la caja I dado que ha salido azul. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que la bola se extraiga de la caja I dado que ha salido azul. Siguiendo la fórmula de Bayes tenemos que

Utilizando los mismos datos del ejercicio anterior, si se sabe que la bola obtenida es roja, ¿cuál es la probabilidad de que provenga de la segunda caja?
Considere los siguientes eventos y sus probabilidades:
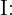 "Se saca una bola de la caja I"
"Se saca una bola de la caja I"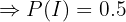
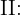 "Se saca una bola de la caja II"
"Se saca una bola de la caja II"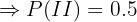
Además, considere el evento
 "Sale una bola roja". El ejercicio nos da también las siguientes probabilidades:
"Sale una bola roja". El ejercicio nos da también las siguientes probabilidades: 
Estamos interesados en conocer 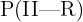 , es decir, la probabilidad de que la bola se extraiga de la caja II dado que ha salido roja. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que la bola se extraiga de la caja II dado que ha salido roja. Siguiendo la fórmula de Bayes tenemos que

Se tienen dos cajas, la primera contiene 3 bolas rojas y 2 azules mientras que la segunda contiene 2 rojas y 8 azules. Se lanza un dado, si se obtiene 1 ó 2 se saca una bola de la primera caja y si se obtiene 3, 4, 5 ó 6 se saca una bola de la segunda. Si se sabe que la bola obtenida es azul, ¿cuál es la probabilidad de que provenga de la primera caja?
Considere los siguientes eventos y sus probabilidades:
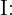 "Se saca una bola de la caja I"
"Se saca una bola de la caja I"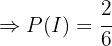
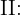 "Se saca una bola de la caja II"
"Se saca una bola de la caja II"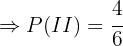
Además, considere el evento
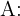 "Sale una bola azul". El ejercicio nos da también las siguientes probabilidades:
"Sale una bola azul". El ejercicio nos da también las siguientes probabilidades: 
Estamos interesados en conocer 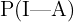 , es decir, la probabilidad de que la bola se extraiga de la caja I dado que ha salido azul. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que la bola se extraiga de la caja I dado que ha salido azul. Siguiendo la fórmula de Bayes tenemos que
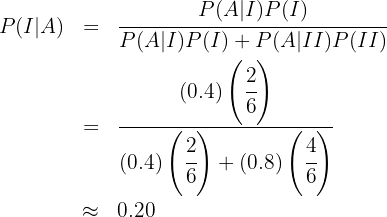
En cierto colegio el 12% de los alumnos utilizan IA para realizar sus trabajos escolares. Un profesor utiliza un detector de uso de IA que acierta el 90% cuando el trabajo fue hecho con IA y que falla un 5% cuando el trabajo no fue realizado con IA. Si el profesor recibe el resultado de que el trabajo fue realizado con IA, ¿cuál es la probabilidad de estar equivocado?
Considere los siguientes eventos y sus probabilidades:
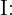 "El estudiante utiliza IA"
"El estudiante utiliza IA"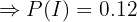
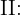 "El estudiante no utiliza IA"
"El estudiante no utiliza IA"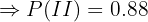
Además, considere el evento
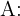 "La prueba es afirmativa". El ejercicio nos da también las siguientes probabilidades:
"La prueba es afirmativa". El ejercicio nos da también las siguientes probabilidades: 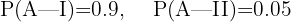
Estamos interesados en conocer  , es decir, la probabilidad de que el alumno no haya utilizado IA dado que la prueba ha resultado afirmativa. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que el alumno no haya utilizado IA dado que la prueba ha resultado afirmativa. Siguiendo la fórmula de Bayes tenemos que

En un restaurante de comida rápida el 30% de los clientes es infantil. Se tienen dos combos a la venta, siendo el combo 1 elegido un 60% por los niños y un 20% por los adultos. Si la orden entregada es un combo 2, ¿cuál es la probabilidad de que el pedido sea para un niño?
Considere los siguientes eventos y sus probabilidades:
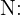 "El cliente es un niño"
"El cliente es un niño"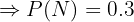
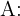 "El cliente es un adulto"
"El cliente es un adulto"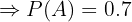
Además, considere el evento
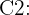 "La orden es un combo 2". El ejercicio nos da también las siguientes probabilidades:
"La orden es un combo 2". El ejercicio nos da también las siguientes probabilidades: 
Estamos interesados en conocer 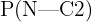 , es decir, la probabilidad de que la orden sea para un niño dado que se trata del combo 2. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que la orden sea para un niño dado que se trata del combo 2. Siguiendo la fórmula de Bayes tenemos que

La probabilidad de que haya un accidente en una fábrica que dispone de alarma es  . La probabilidad de que suene esta sí se ha producido algún incidente es de
. La probabilidad de que suene esta sí se ha producido algún incidente es de 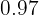 y la probabilidad de que suene si no ha sucedido ningún incidente es
y la probabilidad de que suene si no ha sucedido ningún incidente es  . En el supuesto de que haya funcionado la alarma, ¿cuál es la probabilidad de que no haya habido ningún incidente?
. En el supuesto de que haya funcionado la alarma, ¿cuál es la probabilidad de que no haya habido ningún incidente?
Considere los siguientes eventos y sus probabolidades:
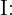 "Se produce un incidente"
"Se produce un incidente"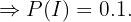
 "No se produce un incidente"
"No se produce un incidente"
Además, considere el evento
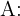 "Suena la alarma" y el evento
"Suena la alarma" y el evento 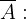 "No suena la alarma". El ejercicio nos da también las siguientes probabilidades:
"No suena la alarma". El ejercicio nos da también las siguientes probabilidades: 
La información anterior puede ser resumida en el siguiente diagrama de árbol:
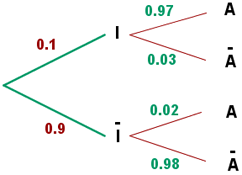
Estamos interesados en conocer 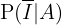 , es decir, la probabilidad de que no haya ocurrido ningún incidente dado que ha sonado la alarma. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que no haya ocurrido ningún incidente dado que ha sonado la alarma. Siguiendo la fórmula de Bayes tenemos que
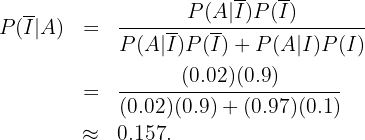
Un análisis de sangre de laboratorio tiene una eficacia del 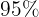 para detectar una determinada enfermedad cuando, de hecho, está presente. Sin embargo, la prueba también arroja un resultado "falso positivo" para el
para detectar una determinada enfermedad cuando, de hecho, está presente. Sin embargo, la prueba también arroja un resultado "falso positivo" para el 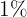 de las personas sanas analizadas. (Es decir, si se hace la prueba a una persona sana, entonces, con una probabilidad de
de las personas sanas analizadas. (Es decir, si se hace la prueba a una persona sana, entonces, con una probabilidad de 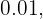 el resultado de la prueba implicará que tiene la enfermedad). Si el
el resultado de la prueba implicará que tiene la enfermedad). Si el 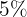 de la población en realidad tiene la enfermedad, ¿cuál es la probabilidad de que una persona tiene la enfermedad dado que el resultado de la prueba es positivo?
de la población en realidad tiene la enfermedad, ¿cuál es la probabilidad de que una persona tiene la enfermedad dado que el resultado de la prueba es positivo?
Considere el evento
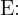 "Tiene la enfermedad" cuya probabilidad es
"Tiene la enfermedad" cuya probabilidad es 
y el evento
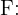 "El resultado es positivo".
"El resultado es positivo".
Sabemos que el laboratorio tiene una eficacia del 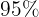 para detectar una determinada enfermedad cuando en realidad se tiene, entonces tenemos que
para detectar una determinada enfermedad cuando en realidad se tiene, entonces tenemos que
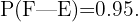
Ahora considere el evento
 "No tiene la enfermedad"
"No tiene la enfermedad"
cuya probabilidad es
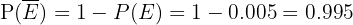
y el evento
 "El resultado es negativo".
"El resultado es negativo".
Las hipótesis nos indican que

Estamos interesados en conocer  , es decir, la probabilidad de que una persona esté enferma dado que la prueba haya dado positivo. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que una persona esté enferma dado que la prueba haya dado positivo. Siguiendo la fórmula de Bayes tenemos que
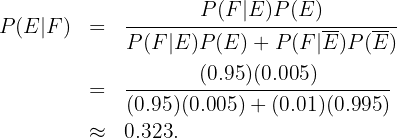
En una cierta etapa de una investigación criminal, el inspector a cargo está convencido en un  de la culpabilidad de cierto sospechoso. Supongamos, sin embargo, que se descubre una nueva prueba que muestra que el delincuente tiene una determinada característica. Si el
de la culpabilidad de cierto sospechoso. Supongamos, sin embargo, que se descubre una nueva prueba que muestra que el delincuente tiene una determinada característica. Si el  de la población posee esta característica, ¿qué tan seguro debe estar el inspector de la culpabilidad del sospechoso ahora si resulta que el sospechoso tiene esta característica?
de la población posee esta característica, ¿qué tan seguro debe estar el inspector de la culpabilidad del sospechoso ahora si resulta que el sospechoso tiene esta característica?
Considere el evento
 "El sospechoso es culpable"
"El sospechoso es culpable"
cuya probabilidad, según el ejercicio, es 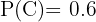 . También, considere el evento
. También, considere el evento
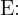 "Coincide con la evidencia alguien inocente".
"Coincide con la evidencia alguien inocente".
De las hipótesis se sigue que 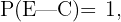 es decir, alguien que coincide con la evidencia dado que es culpable siempre es verdadero. Además, si el evento
es decir, alguien que coincide con la evidencia dado que es culpable siempre es verdadero. Además, si el evento
 "El sospechoso es inocente",
"El sospechoso es inocente",
entonces se sigue que
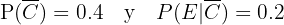
Estamos interesados en conocer 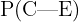 , esto es, la probablidad de que sea culpable dado que coincide con la nueva evidenica. Siguiendo la fórmula de Bayes tenemos que
, esto es, la probablidad de que sea culpable dado que coincide con la nueva evidenica. Siguiendo la fórmula de Bayes tenemos que
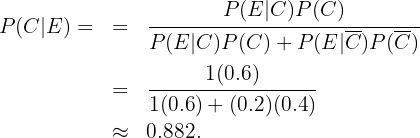
Una fábrica de clavos dispone de  máquinas que elaboran el
máquinas que elaboran el  y
y  de los clavos que producen. El porcentaje de clavos defectuosos de cada máquina es del
de los clavos que producen. El porcentaje de clavos defectuosos de cada máquina es del  y
y  , respectivamente. Si se selecciona al azar un clavo de la producción y este fue defectuoso, ¿cuál es la probabilidad de que haya sido fabricado por la máquina
, respectivamente. Si se selecciona al azar un clavo de la producción y este fue defectuoso, ¿cuál es la probabilidad de que haya sido fabricado por la máquina  ?
?
Considere los siguientes eventos con sus respectivas probabilidades:
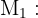 "Clavos fabricados por la máquina
"Clavos fabricados por la máquina  "
"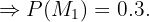
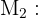 "Clavos fabricados por la máquina
"Clavos fabricados por la máquina  "
"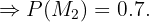
 "Los clavos fabricados son defectuosos"
"Los clavos fabricados son defectuosos" 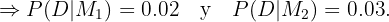
Estamos interesados en conocer
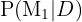 , es decir, la probabilidad de que un clavo seleccionado al azar de la producción haya sido fabricado por la máquina
, es decir, la probabilidad de que un clavo seleccionado al azar de la producción haya sido fabricado por la máquina  dado que ha salido defectuoso. Siguiendo la fórmula de Bayes tenemos que
dado que ha salido defectuoso. Siguiendo la fórmula de Bayes tenemos que

El  de los empleados de una empresa son ingenieros y otro
de los empleados de una empresa son ingenieros y otro  son economistas. El
son economistas. El 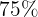 de los ingenieros ocupan un puesto directivo y el
de los ingenieros ocupan un puesto directivo y el  de los economistas también, mientras que los no ingenieros y los no economistas solamente el
de los economistas también, mientras que los no ingenieros y los no economistas solamente el  ocupa un puesto directivo. ¿Cuál es la probabilidad de que un empleado directivo elegido al azar sea ingeniero?
ocupa un puesto directivo. ¿Cuál es la probabilidad de que un empleado directivo elegido al azar sea ingeniero?
Considere los siguientes eventos y sus probabilidades:
 "Los empleados son ingenieros"
"Los empleados son ingenieros" 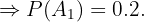
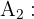 "Los empleados son economistas"
"Los empleados son economistas" 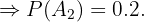
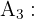 "Los empleados tienen otra carrera"
"Los empleados tienen otra carrera"
Además, considere el evento
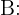 "el empleado ocupa un puesto directivo". El ejercicio nos da también las siguientes probabilidades:
"el empleado ocupa un puesto directivo". El ejercicio nos da también las siguientes probabilidades:

La información anterior puede ser resumida en el siguiente diagrama de árbol:

Estamos interesados en conocer 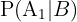 , es decir, la probabilidad de que un empleado sea ingeniero dado que a priori sabemos que es directivo. Siguiendo la fórmula de Bayes tenemos que
, es decir, la probabilidad de que un empleado sea ingeniero dado que a priori sabemos que es directivo. Siguiendo la fórmula de Bayes tenemos que
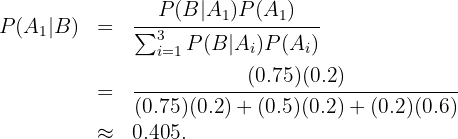
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3