Resuelve los siguientes problemas de probabilidad
Halla la probabilidad de que al lanzar al aire dos monedas, salgan:
A Dos caras
B Dos cruces
C Una cara y una cruz
A Dos caras.

Multiplicamos la probabilidad que tiene el suceso de que caiga una cara en una moneda (1/2), por la probabilidad del mismo suceso en la otra moneda (1/2), debido a que son sucesos independientes
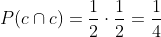
B Dos cruces.
El suceso de que caiga una cruz en una moneda y también cruz en la otra, son sucesos independientes y cada uno tiene una probabilidad de (1/2) como lo observamos en el esquema. Debido a esto, se multiplican ambas probabilidades
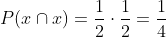
C Una cara y una cruz.
La probabilidad de sacar una cara y una cruz, se refiere a las siguientes dos posibilidades: cara y cruz, o cruz y cara. Significa que primero debemos sacar la probabilidad de cada opción (1/2)(1/2) y después sumarlas, para tener el resultado, observa:
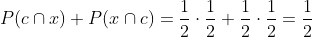
Calcular la probabilidad de sacar exactamente dos cruces al tirar una moneda tres veces.
Los resultados posibles por lanzamiento son cara (C) o cruz (X).
Primero podemos sacar las formas en que pueden salir dos cruces (X) en tres lanzamientos.
De tres resultados posibles n=3, veamos de cuántas formas r=2 de ellos son iguales, es decir calculemos el total de grupos de dos elementos (resultados iguales) que se pueden extraer de un total de tres elementos (resultados posibles).
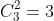
como vemos son 3. Con la finalidad de ser más claros aquí mostramos las 3 formas
XXC, XCX, CXX
ahora bien, el total de formas que pueden salir las monedas al lanzarlas tres veces, pensando en que son dos opciones por cada una es 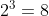
Por lo tanto, la probabilidad de sacar dos cruces exactamente al lanzar una moneda tres veces es
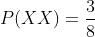
Halla la probabilidad de que al levantar unas fichas de dominó se obtenga un número de puntos mayor que 9 o que sea múltiplo de 4.
En el conjunto A ponemos a las fichas donde el total de puntos de cada una es mayor a nueve, y en el B a las fichas donde la cantidad de puntos de cada una es múltiplo de cuatro:
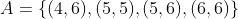
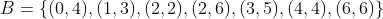
en este caso observamos que la ficha (6,6) pertenece a ambos conjuntos, o en otras palabras 

Ahora, tomando en cuenta que existen 28 fichas de dominó, los valores quedan de la siguiente forma:
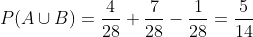
Un dado está trucado, de forma que las probabilidades de obtener las distintas caras son proporcionales a los números de estas. Hallar:
A La probabilidad de obtener el 6 en un lanzamiento
B La probabilidad de conseguir un número impar en un lanzamiento
A La probabilidad de obtener el 6 en un lanzamiento
Ya que el dado está trucado, la probabilidad de cada cara es proporcional al número de la cara correspondiente.
Por ejemplo 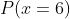
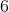
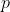
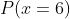
Si por otro lado sumamos las probabilidades de cada cara tenemos lo siguiente
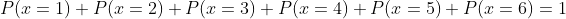
y entonces
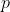
llevándonos a que 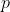
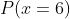
B La probabilidad de conseguir un número impar en un lanzamiento
En este caso sólo es necesario sumar las probabilidades de que conseguir todos los impares posibles.
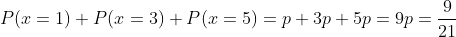
Se lanzan dos dados al aire y se anota la suma de los puntos obtenidos. Se pide:
A La probabilidad de que salga el 7
B La probabilidad de que el número obtenido sea par
C La probabilidad de que el número obtenido sea múltiplo de tres
A La probabilidad de que salga el 7
Agrupamos a todas las posibilidades donde la suma sea siete

nos damos cuenta que son 6 formas posibles, y como hay 36 formas posibles distintas en las que pueden caer dos dados, entonces:
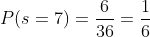
B La probabilidad de que el número obtenido sea par
Las parejas para que el número obtenido sea par son
(1,1)
(1,3), (2,2),(3,1)
(1,5),(2,4),(3,3),(4,2),(5,1)
(2,6),(3,5),(4,4),(5,3),(6,2)
(4,6),(5,5),(6,4)
(6,6)
que son 18, significa que la probabilidad de que el resultado obtenido sea par es
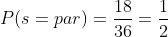
C La probabilidad de que el número obtenido sea múltiplo de tres
Nos damos cuenta que cada una de estas parejas suman a algún múltiplo de tres
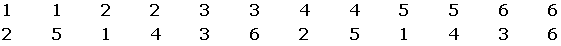
y son 12 de ellas, entonces
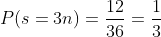
aquí en representa a los múltiplos de 3.
Se lanzan tres dados. Encontrar la probabilidad de que:
A Salga 6 en todos
B Los puntos obtenidos sumen 7
A Salga 6 en todos
Solamente existe una forma de que salga seis en todos (6,6,6), y si consideramos que hay 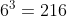
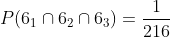
B Los puntos obtenidos sumen 7
Aquí se encuentran las formas en que pueden caer los dados, donde la suma de los puntos es siete:

y con esta lista, nos damos cuenta de que existen 15 distintas formas para que la suma sea 7, entonces la probabilidad buscada queda:
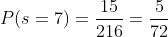
Busca la probabilidad de que al echar un dado al aire, salga:
A Un número par
B Un múltiplo de tres
C Mayor que cuatro
A Un número par
Para que sea par, se tienen las siguientes opciones: 2,4,6.
Significa que hay 3 formas de las 6 posibles, de esta manera la probabilidad queda
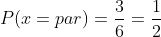
B Un múltiplo de tres
En esta caso los múltiplos de tres son: 3 y 6. Por lo tanto hay 2 formas para que sea múltiplo de 3, y 6 formas en que puede caer un dado
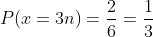
C Mayor que cuatro
En este caso los mayores que cuatro son 5 y 6, llevándonos a que la probabilidad es
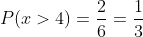
Se sacan dos bolas de una urna que se compone de una bola blanca, otra roja, otra verde y otra negra. Describir el espacio muestral cuando:
A La primera bola se devuelve a la urna antes de sacar la segunda
B La primera bola no se devuelve
A La primera bola se devuelve a la urna antes de sacar la segunda
La primer bola puede ser cualquiera de las cuatro B,R,V,N y al momento de registrar la que salió y regresarla a la urna, puede salir nuevamente cualquiera de las cuatro, significa que por ejemplo si al principio salió B, entonces con la segunda extracción se puede tener BB,BR,BV o BN, y así sucesivamente con las demás opciones, quedando nuestro espacio muestral como
E = {BB, BR, BV, BN, RB, RR, RV, RN, VB, VR, VV, VN, NB, NR, NV, NN}
B La primera bola no se devuelve
Como la bola que se saca al principio no se devuelve, entonces en la segunda extracción debe salir alguna de las cuatro restantes, significa que ya no es posible que se repita la bola, quedando el espacio muestral como
E = { BR, BV, BN, RB, RV, RN, VB, VR, VN, NB, NR, NV}
Una urna tiene ocho bolas rojas, 5 amarilla y siete verdes. Se extrae una al azar de que:
A Sea roja
B Sea verde
C Sea amarilla
D No sea roja
E No sea amarilla
A Sea roja
De 20 bolas en total, hay 8 rojas. Entonces la probabilidad queda
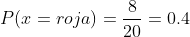
B Sea verde
Como hay 7 bolas verdes la probabilidad queda
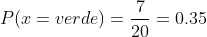
C Sea amarilla
De las 20 bolas, hay 5 amarillas, entonces
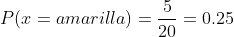
D No sea roja
Ya que debemos calcular la probabilidad de que NO sea roja, entonces podemos restarle al total (1), la probabilidad de que SI sea roja, quedando la probabilidad buscada asi
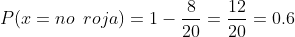
E No sea amarilla
Aquí ocupamos el mismo razonamiento que en el inciso anterior
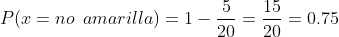
Una urna contiene tres bolas rojas y siete blancas. Se extraen dos bolas al azar. Escribir el espacio muestral y hallar la probabilidad de:
A Extraer las dos bolas con reemplazamiento
B Sin reemplazamiento
A Extraer las dos bolas con reemplazamiento
Primero describamos al espacio muestra. Al haber dos tipos de bolas, rojas (R) o blancas (B), en nuestra primera extracción podemos tener a cualquiera de las dos bolas, y como la cantidad de cada una de ellas es mayor que uno, entonces (con reemplazo o sin reemplazo), en la segunda extracción también se puede obtener cualquiera de las dos, quedando el espacio muestra de la siguiente forma
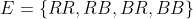
Ahora, al extraer una bola y posteriormente regresarla a la urna (reemplazarla), las condiciones de la primera y la segunda extracción son exactamente iguales, significa que son sucesos independientes, aquí podemos aplicar la siguiente fórmula que funciona para sucesos independientes
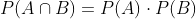
Primer extracción R, segunda R
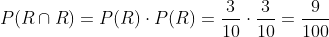
Primer extracción R, segunda B
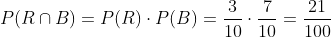
Primer extracción B, segunda R
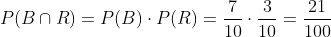
Primer extracción B, segunda B
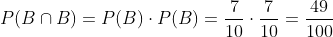
B Sin reemplazamiento
En este caso como no hay reemplazo, la extracción de la primer bola modifica las condiciones de la segunda extracción, por ejemplo si en la primer extracción se obtuvo bola Roja, significa que en la segunda extracción hay una bola Roja menos en la urna, es decir 2 Rojas, y además una bola menos en total, es decir 9, esto significa que son sucesos dependientes.
Veamos todas las opciones
Primer extracción R, segunda R
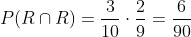
Primer extracción R, segunda B
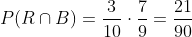
Primer extracción B, segunda R
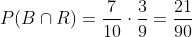
Primer extracción B, segunda B
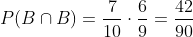
Se extrae una bola de una urna que contiene 4 bolas rojas, 5 blancas y 6 negras
A ¿cuál es la probabilidad de que la bola sea roja o blanca?
B ¿Cuál es la probabilidad de que no sea blanca?
A ¿cuál es la probabilidad de que la bola sea roja o blanca?
Aquí se trata de sucesos donde no hay elementos en común, así que de la fórmula

solamente nos quedamos con
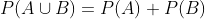
de esta manera, la probabilidad de que la bola sea roja o blanca es
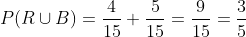
B ¿Cuál es la probabilidad de que no sea blanca?
La probabilidad de que la bola NO sea blanca es
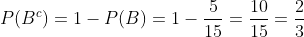
En una clase hay 10 alumnas rubias, 20 morenas, cinco alumnos rubios y 10 morenos. Un día asisten 44 alumnos, encontrar la probabilidad de que el alumno que falta:
A Sea hombre
B Sea mujer morena
C Sea hombre o mujer
A Sea hombre
En la siguiente tabla tenemos la información del problema
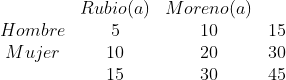
y de aquí podemos ver que hay 15 hombres y 45 alumnos, entonces la probabilidad de que sea hombre es
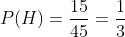
B Sea mujer morena
Hay 20 mujeres morenas, entonces
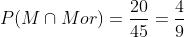
C Sea hombre o mujer
Aquí la probabilidad es la total
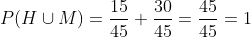
En un sobre hay 20 papeletas, ocho llevan dibujado un coche las restantes son blancas. Hallar la probabilidad de extraer al menos una papeleta con el dibujo de un coche:
A Si se saca una papeleta
B Si se extraen dos papeletas
C Si se extraen tres papeletas
A Si se saca una papeleta
Como hay 8 papeletas con coche y 20 papeletas en total, la probabilidad de extraer una papeleta con coche es
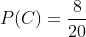
B Si se extraen dos papeletas
Al extraer dos papeletas, puede salir BB, CB, BC o CC. Podríamos sacar la probabilidad de CB, BC, CC y después sumarlas, sin embargo es más práctico calcular la probabilidad de BB y el valor obtenido restarlo al 1
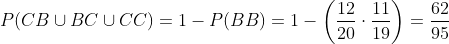
C Si se extraen tres papeletas
Aquí podemos basarnos en la misma deducción del inciso anterior
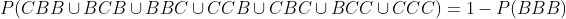
entonces
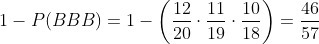
Los estudiantes A y B tienen respectivamente probabilidades 1/2 y 1/5 de suspender un examen. La probabilidad de que suspendan el examen simultáneamente es de 1/10. Determinar la probabilidad de que al menos uno de los dos estudiantes suspenda el examen.
Los estudiantes A y B tienen respectivamente probabilidades 1/2 y 1/5 de suspender un examen. La probabilidad de que suspendan el examen simultáneamente es de 1/10. Determinar la probabilidad de que al menos uno de los dos estudiantes suspenda el examen.
Son sucesos compatibles, es decir que la probabilidad de eventos simultáneos es distinta de cero. Calculamos entonces la probabilidad de la siguiente manera
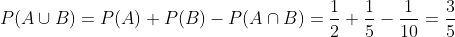
Dos hermanos salen de casa. El primero mata un promedio de 2 piezas cada 5 disparos y el segundo una pieza cada 2 disparos. Si los dos disparan al mismo tiempo a una misma pieza, ¿cuál es la probabilidad de que la maten?
La probabilidad de que el primer hermano mate a una pieza es
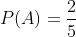
la probabilidad de que mate el segundo hermano a una pieza es
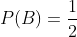
por otro lado, la probabilidad de que ambos maten al mismo tiempo cada uno a una pieza es
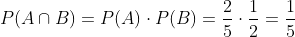
y entonces, si al mismo tiempo disparan a la misma pieza y el hermano A o el hermano B la maten, es
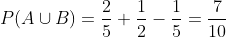
Una clase consta de 10 hombres y 20 mujeres; la mitad de los hombres y la mitad de las mujeres tienen los ojos castaños. Determinar la probabilidad de que una persona elegida al azar sea un hombre o tenga los ojos castaños.

Aquí debemos observar que hay tanto hombres 10 como de ojos castaños 15, además de hombres con ojos castaños 5, así que la probabilidad de que sea hombre o tenga ojos castaños se calcula con la fórmula

hagamos el cálculo
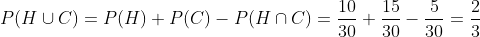
La probabilidad de que un hombre viva 20 años es ¼ y la de que su mujer viva 20 años es 1/3. Se pide calcular la probabilidad:
A De que ambos vivan 20 años.
B De que el hombre viva 20 años y su mujer no.
C De que ambos mueran antes de los 20 años.
A De que ambos vivan 20 años
Lo que ocurra con uno, no afecta lo que ocurra con el otro, debido a eso son suceso independientes, así que podemos calcular la probabilidad de la siguiente manera
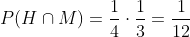
B De que el hombre viva 20 años y su mujer no
Aquí también son sucesos independientes entonces los podemos trabajar como tal, solamente agregamos la fórmula que calcula la probabilidad de que NO ocurra algo
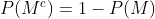
entonces queda
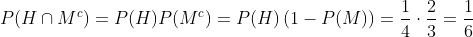
C De que ambos mueran antes de los 20 años
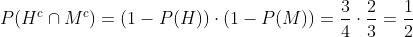
Calcular la probabilidad de sacar exactamente dos cruces al tirar una moneda cuatro veces.
Los resultados posibles por lanzamiento son cara (C) o cruz (X).
Primero podemos sacar las formas en que pueden salir dos cruces (X) en cuatro lanzamientos.
De cuatro resultados posibles n=4, veamos de cuántas formas r=2 de ellos son iguales, es decir calculemos el total de grupos de dos elementos (resultados iguales) que se pueden extraer de un total de cuatro elementos (resultados posibles).
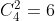
como vemos son 6. Con la finalidad de ser más claros aquí mostramos las 6 formas
XXCC, XCXC, XCCX, CXXC, CXCX, CCXX
ahora bien, el total de formas que pueden salir las monedas al lanzarlas cuatro veces, pensando en que son dos opciones por cada una es 
Por lo tanto, la probabilidad de sacar dos cruces exactamente al lanzar una moneda cuatro veces es
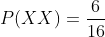
Un grupo de 10 personas se sienta en un banco. ¿Cuál es la probabilidad de que dos personas fijadas de antemano se sienten juntas.
Para conocer todas las formas que se tienen de colocar a 10 personas en 10 lugares, usamos la permutación

y ahora, para saber el total de formas donde 2 seleccionadas previamente se sienten juntas, podemos pensar en que al sentarse juntas ocupan un lugar de nueve posibles, de esta manera, las formas en que nueve personas se pueden sentar ocupando 9 lugares es
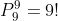
y como cuando se sientan juntas puede ser de dos maneras posibles: ab ó ba, entonces el total de formas en que dos personas seleccionadas previamente se pueden sentar juntas en 10 lugares posibles es 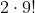
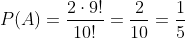
Se extraen cinco cartas de una baraja de 52. Hallar la probabilidad de extraer:
A 4 ases
B 4 ases y un rey
C 3 cincos y 2 sotas
D Un 9, 10, sota, caballo y rey en cualquier orden
E 3 de un palo cualquiera y 2 de otro
F Al menos un as
A 4 ases
Primero, el total de formas distintas que se pueden generar de 52 cartas, al agruparlas de 5 en 5 son
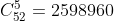
Ahora, de 4 ases formamos a un grupo (sin importar el orden) de 4, quedando una forma 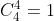
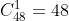
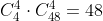
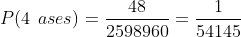
B 4 ases y un rey
Para 4 ases solamente hay una posiblidad y para que se tenga rey hay cuatro posibilidades. En otras palabras, multiplicamos las posibilidades de 4 ases por las del rey 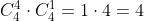
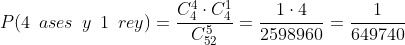
C 3 cincos y 2 sotas
Hay 4 cincos y de ahí queremos a 3 de ellos, por otro lado hay 4 sotas y de ahí queremos a 2, entonces
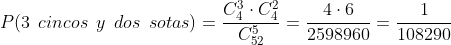
D Un 9, 10, sota, caballo y rey en cualquier orden
Por cada carta hay 4 posibilidades y como son 5 cartas tenemos 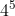
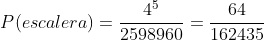
E 3 de un palo cualquiera y 2 de otro
Para que tengamos 3 de un palo (13 cartas) entonces se calcula 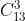
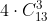
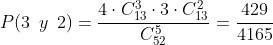
F Al menos un as
Primero calculemos la probabilidad de que NO salga as, significa que quitaremos a todos los ases
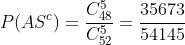
Y entonces la probabilidad de que salga al menos un as, es el resto
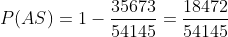
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3