La combinatoria es una rama emocionante de las matemáticas que se enfoca en contar, organizar y analizar distintas formas en que los objetos pueden combinarse o agruparse. Desde la resolución de acertijos hasta la optimización de estrategias, la combinatoria tiene una amplia gama de aplicaciones en la vida cotidiana y en diversas disciplinas, como la informática, la estadística, la biología y la teoría de juegos.
En esta colección de ejercicios y problemas de combinatoria, te sumergirás en el fascinante mundo de las permutaciones, combinaciones, variaciones, conjuntos y mucho más. Cada desafío plantea una oportunidad única para fortalecer tu pensamiento analítico, habilidades de resolución de problemas y comprensión de conceptos matemáticos fundamentales.
Tanto si eres nuevo en la combinatoria como si estás buscando perfeccionar tus habilidades, esta selección de ejercicios te guiará desde los conceptos básicos hasta desafíos más avanzados. Prepárate para explorar patrones intrigantes, estrategias ingeniosas y abordajes creativos para resolver problemas que te desafiarán a pensar de manera única.
Puestos en club de fútbol
¿De cuántas formas diferentes se pueden cubrir los puestos de presidente, vicepresidente y tesorero de un club de fútbol sabiendo que hay  posibles candidatos?
posibles candidatos?
No entran todos los elementos
Sí importa el orden
No se repiten los elementos
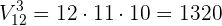
Combinatoria de 5 letras
Con las letras de la palabra libro. ¿Cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
La palabra empieza por i u o seguida de las  letras restantes tomadas de
letras restantes tomadas de  en
en  .
.
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos

Combinatorias con los colores del arco iris
¿De cuántas formas pueden mezclarse los siete colores del arco iris tomándolos de tres en tres?
No entran todos los elementos
No importa el orden. Consideraremos mezclas iguales aquellas que contengan los mismos colores pero distinto orden.
No se repiten los elementos
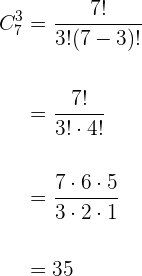
Combinatoria: 5 cifras con restricción
¿Cuántos números de cinco cifras distintas se pueden formar con las cifras impares 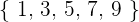 ? ¿Cuántos de ellos son mayores de
? ¿Cuántos de ellos son mayores de  ?
?
¿Cuántos de ellos son mayores de 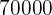 ?
?
Sí entran todos los elementos 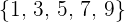
Sí importa el orden
No se repiten los elementos, ya que especificamos que las cifras deben de ser distintas.

Si es impar, sólo puede empezar por 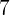 o
o  . Entonces, si restringimos la primer cifra a estas dos posibilidades únicamente, tenemos
. Entonces, si restringimos la primer cifra a estas dos posibilidades únicamente, tenemos

Combinatoria: 3 cifras con restricción
¿Cuántos números de tres cifras distintas se pueden formar con las cifras 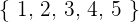 ? ¿Cuántos de ellos son pares?
? ¿Cuántos de ellos son pares?
No entran todos los elementos 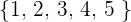
Sí importa el orden
No se repiten los elementos, ya que especificamos que las cifras deben de ser distintas.

Si es par, sólo puede terminar por  o
o 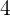 . Entonces, si restringimos la última cifra a estas dos posibilidades únicamente, tenemos
. Entonces, si restringimos la última cifra a estas dos posibilidades únicamente, tenemos
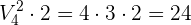
Liguilla de 4 equipos
¿Cuántos partidos distintos se pueden realizar dados cuatro equipos de futbol?
No entran todos los elementos (sólo se toman dos equipos)
No importa el orden (Es lo mismo A vs B que B vs A).
No se repiten los elementos
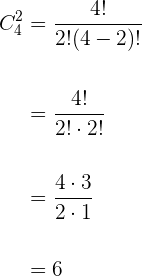
Número de saludos en una reunión
A una reunión asisten  personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
No entran todos los elementos
No importa el orden
No se repiten los elementos
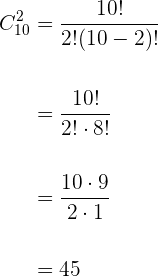
Elementos de cinco cifras usando solo tres números.
Con las cifras  ,
,  y
y  . ¿Cuántos números de cinco cifras pueden formarse? ¿Cuántos son pares?
. ¿Cuántos números de cinco cifras pueden formarse? ¿Cuántos son pares?
Sí entran todos los elementos:  .
.
Sí importa el orden
Sí se repiten los elementos
 .
.
Dados los dígitos  ,
,  y
y  , un número solamente puede ser par si terminar con
, un número solamente puede ser par si terminar con  . Así, la cantidad de números pares está dada por
. Así, la cantidad de números pares está dada por
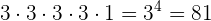
Como ganar la lotería
¿Cuántas apuestas de Lotería Primitiva de una columna han de rellenarse para asegurarse el acierto de los seis resultados, de  ?
?
No entran todos los elementos
No importa el orden
No se repiten los elementos
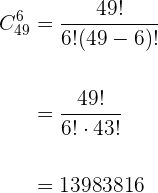
Fútbol: Cuadro deportivo
¿De cuántas formas pueden colocarse los  jugadores de un equipo de fútbol teniendo en cuenta que el portero no puede ocupar otra posición distinta de la portería mientras que los otros
jugadores de un equipo de fútbol teniendo en cuenta que el portero no puede ocupar otra posición distinta de la portería mientras que los otros  pueden jugar en cualquier otra posición que no sea portero?
pueden jugar en cualquier otra posición que no sea portero?
Notemos que disponemos de  jugadores que pueden ocupar
jugadores que pueden ocupar  posiciones distintas.
posiciones distintas.
Sí entran todos los elementos.
Sí importa el orden
No se repiten los elementos.

Combinatoria de pulsaciones en código Morse
Con el punto y raya del sistema Morse, ¿cuántas señales distintas se pueden enviar, usando como máximo cuatro pulsaciones?
Dado que tomamos como máximo cuatro pulsaciones, debemos considerar y sumar una, dos, tres y cuatro pulsaciones. Entonces:
No entran todos los elementos en un caso y sí entran en lo otros
Sí importa el orden
Sí se repiten los elementos
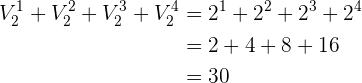
Ejercicio sobre cambio de asientos con restricción
Una mesa presidencial está formada por ocho persona. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?
Nota: Supongamos que, si todos están sentados, luego deciden levantarse y sentarse en la silla de su lado derecho (desplazarse un lugar), entonces esta es una configuración o 'forma' diferente a la anterior.
Se forman dos grupos:
El primero de dos personas. Ya sea 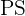 o
o 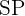 (
( ).
).
El segundo sería considerado como un grupo de  personas. Este grupo está conformado por las 6 personas restante y el otro grupo considerado arriba.
personas. Este grupo está conformado por las 6 personas restante y el otro grupo considerado arriba.
Basta pensar en el grupo formado por el presidente y el secretario como una única persona (pues siempre van juntos).
En los dos se cumple que:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
No es necesario fijar una posición, pues desplazar a todos los individuos un lugar produce una permutación distinta
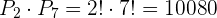
Otro ejercicio sobre cambio de asientos con restricción
Se tiene una fila de asientos para ocho persona. ¿De cuántas formas distintas se pueden sentar, si dos de ellas no pueden estar juntos?
Se forman tres grupos:
El primero de dos personas que no deben estar juntos, las juntamos y lo consideramos como los casos no deseados.
El segundo sería considerado como un grupo de  personas. Este grupo está conformado por las 6 personas restante y el otro grupo considerado arriba y también lo consideramos como los casos no deseados.
personas. Este grupo está conformado por las 6 personas restante y el otro grupo considerado arriba y también lo consideramos como los casos no deseados.
En los dos se cumple que:
Sí entran todos los elementos
Sí importa el orden
No se repiten los elementos
No es necesario fijar una posición, pues desplazar a todos los individuos un lugar produce una permutación distinta
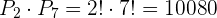
El tercero sería considerado todas las posibilidades de sentar a las ocho personas, esto contiene los casos deseados y no deseados
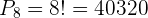
Para obtener las posibilidades donde nunca están juntas estas dos personas, restamos los casos no deseados del total de casos
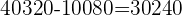
Número de triángulos en un pentágono
¿Cuántas diagonales tiene un pentágono y cuántos triángulos se pueden formar con sus vértices?
Son  , a las que tenemos que restar los lados que determinan
, a las que tenemos que restar los lados que determinan  rectas que no son diagonales.
rectas que no son diagonales.
No entran todos los elementos
No importa el orden
No se repiten los elementos
e tenemos que restar los lados que determinan
 rectas que no son diagonales.
rectas que no son diagonales. 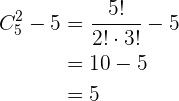
La cantidad de triángulos son la cantidad de tres puntos que podemos tomar de los cinco que conforman el pentágono, en donde
No entran todos los elementos
No importa el orden
No se repiten los elementos
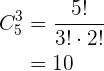
Ejercicios de combinatoria con restricciones
Un grupo, compuesto por cinco hombres y siete mujeres, forma un comité de dos hombres y tres mujeres. De cuántas formas puede formarse, si:
1 Puede pertenecer a él cualquier hombre o mujer.
2 Una mujer determinada debe pertenecer al comité.
3 Dos hombres determinados no pueden estar en el comité.
1 Puede pertenecer a él cualquier hombre o mujer.

2 Una mujer determinada debe pertenecer al comité.

3 Dos hombres determinados no pueden estar en el comité.

Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3