Capítulos

Ley de Laplace
Esta ley establece la probabilidad de que suceda un suceso o que ganes en un juego de azar.
Si lanzamos un dado, debe considerarse que hay igual posibilidad que salga cualquiera de las caras numeradas del 1 al 6, entonces la probabilidad de que salga cualquier número será  .
.
Si ahora queremos saber cual es la probabilidad de que salga un número par el resultado seria 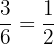 , debido a que
, debido a que 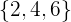 son los resultados pares.
son los resultados pares.
En general la probabilidad de que un suceso es la razón entre el número de casos favorables y el número total de casos posibles y esa es la ley de Laplace.
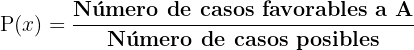
Sucesos incompatibles
Son dos sucesos que no pueden presentarse al mismo tiempo.
Ejemplo:
Se realiza una encuesta a alumnos universitarios para ver cuántos fuman y no fuman, entonces  es el conjunto de los fumadores y
es el conjunto de los fumadores y  de los no fumadores por lo tanto:
de los no fumadores por lo tanto:
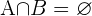
Porque una persona puede ser fumador y no fumador a la vez.
Entonces si escojo un alumno al azar quiero saber cuál es la probabilidad de que fume o no fume y uso la formula:
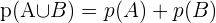
Sucesos compatibles
Son dos sucesos que pueden presentarse al mismo tiempo.
Ejemplo:
En una universidad hay alumnos que estudian inglés, francés o los dos idiomas. Si  son los que estudian inglés y
son los que estudian inglés y  los que estudian francés, entonces
los que estudian francés, entonces 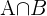 son los que estudian inglés y francés y por lo tanto:
son los que estudian inglés y francés y por lo tanto:
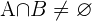
Ahora si escojo un alumno al azar y quiero saber la probabilidad de que estudie ingles o francés uso la formula:
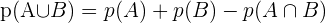
Probabilidad condicionada
Es cuando la probabilidad un suceso  se puede ver afectado por otro suceso
se puede ver afectado por otro suceso  .
.
Ejemplo:
Imagina que juegas con otra persona a lanzar una moneda tres veces, tu ganas si cae cara y pierdes si cae lo contrario. Para triunfar debes ganar al menos dos de tres volados.
Si represento con 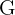 un volado ganado y con
un volado ganado y con uno perdido, entonces los resultados serían
uno perdido, entonces los resultados serían 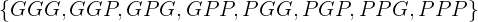 .
.
Para ganar el juego, debe ocurrir 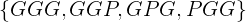 , por lo tanto la probabilidad de ganar es
, por lo tanto la probabilidad de ganar es 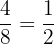 .
.
Supongamos que se pierde el primer volado, de manera que que quedan dos por jugar. ¿Cuál es la probabilidad de ganar?
Usaremos la formula:
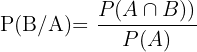
Llamemos  al suceso de ganar y
al suceso de ganar y  al suceso de perder el primer volado cuyos resultados serían
al suceso de perder el primer volado cuyos resultados serían 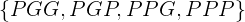 , entonces
, entonces 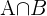 sería el suceso de ganar y perder el primer volado cuyo resultado sería
sería el suceso de ganar y perder el primer volado cuyo resultado sería 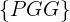 ,
, 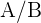 es el suceso de ganar si ya perdiste el primer volado.
es el suceso de ganar si ya perdiste el primer volado.
Con base en los resultados encontrados anteriormente 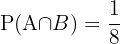 ,
, 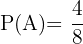 entonces:
entonces:
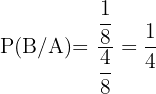
Por lo tanto la probabilidad de ganar es  .
.
Sucesos independientes
Son aquellos donde no se afectan uno con el otro.
Ejemplo:
Dos personas van a lanzar un objeto al mismo blanco, pero la primera persona que llamaremos  tiene una probabilidad de
tiene una probabilidad de  de dar en el blanco y la segunda persona que llamaremos
de dar en el blanco y la segunda persona que llamaremos  tiene una probabilidad de
tiene una probabilidad de  de dar en el blanco ¿Cuál es la probabilidad de que las dos personas den en el blanco?
de dar en el blanco ¿Cuál es la probabilidad de que las dos personas den en el blanco?
Entonces tenemos 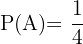 ,
, 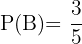 y hay que calcular
y hay que calcular  usando la siguiente fórmula:
usando la siguiente fórmula:
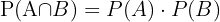
El resultado sería 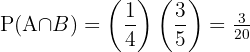
Sucesos dependientes
Son aquellos donde se afectan uno con el otro.
Ejemplo:
En una población el  % de las personas sufren una enfermedad. Se dispone de un procedimiento para diagnosticarla, pero no es completamente confiable, ya que da positivo en
% de las personas sufren una enfermedad. Se dispone de un procedimiento para diagnosticarla, pero no es completamente confiable, ya que da positivo en  % de los casos que las personas que la padecen. ¿Cuál es la probabilidad de que padezca la enfermedad y dé positivo?
% de los casos que las personas que la padecen. ¿Cuál es la probabilidad de que padezca la enfermedad y dé positivo?
Llamemos  al suceso que da positivo la enfermedad y
al suceso que da positivo la enfermedad y  al suceso de padecer la enfermedad, entonces
al suceso de padecer la enfermedad, entonces 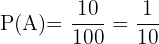 ,
, 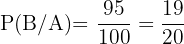 y hay que calcular
y hay que calcular 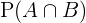 usamos la fórmula:
usamos la fórmula:
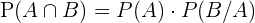
Por lo tanto:
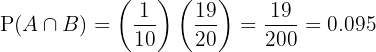
El resultado es 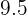 % de probabilidad.
% de probabilidad.
Diferencia de sucesos
Son aquellos que pueden estar o no estar relacionados y queremos la probabilidad de uno sin tener nada que ver con el otro.
Ejemplo:
Se lanza un dado y queremos calcular la probabilidad de que salga un número par, pero que no sea múltiplo de  , entonces llamamos
, entonces llamamos  al suceso de que sea un número par,
al suceso de que sea un número par,  al suceso de que sea múltiplo de
al suceso de que sea múltiplo de  y tendríamos
y tendríamos 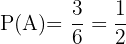 ,
, 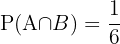 ya que
ya que 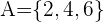 ,
, 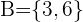 ,
, 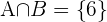 usamos la fórmula:
usamos la fórmula:
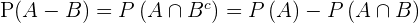
Por lo tanto:
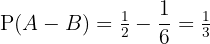
Teorema de la probabilidad total
Este se aplica cuando tienes varios sucesos independientes o que no tienen nada que ver entre ellos, pero todos se relacionan con otro suceso del cual quieres saber su probabilidad.
Si tenemos un suceso  y sean
y sean 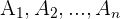 eventos mutuamente excluyentes. Entonces se aplica la fórmula:
eventos mutuamente excluyentes. Entonces se aplica la fórmula:
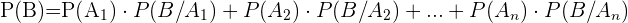
Ejemplo:
Una fabrica utiliza tres maquinas 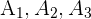 para producir ciertos artículos. Supongamos que:
para producir ciertos artículos. Supongamos que:
La maquina 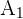 produce el 55% de todos los artículos, de los cuales el 2% son defectuosos.
produce el 55% de todos los artículos, de los cuales el 2% son defectuosos.
La maquina 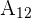 produce el 25% de todos los artículos, de los cuales el 4% son defectuosos.
produce el 25% de todos los artículos, de los cuales el 4% son defectuosos.
La maquina 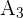 produce el 20% de todos los artículos, de los cuales el 5% son defectuosos.
produce el 20% de todos los artículos, de los cuales el 5% son defectuosos.
¿Cuál es la probabilidad de que si se escoge un artículo este sea defectuoso?
Tenemos que  es el suceso de que el artículo sea defectuoso, entonces:
es el suceso de que el artículo sea defectuoso, entonces:
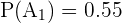 ,
, 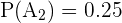 ,
, 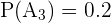 ,
, 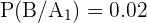 ,
, 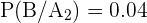 y
y 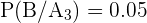
Aplicamos la fórmula:
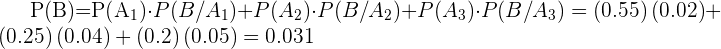
Entonces la probabilidad es de 3.1%.
Teorema de Bayes
Este teorema nos facilita ejercicios de probabilidad condicional con varios sucesos.
Si tenemos un suceso  y sean
y sean 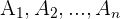 eventos mutuamente excluyentes se cumple la formula:
eventos mutuamente excluyentes se cumple la formula:
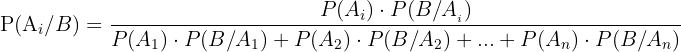
En una fábrica trabajan tres empleados Andrés, Beto y Carlos. Andrés realiza el 50% de la producción, Beto el 30% y Carlos el 20%. Andrés tiene 1% de probabilidad de que lo haga mal; cuando lo hace Beto, hay 2% de que lo haga mal y en el caso de Carlos hay 3% de probabilidad que lo haga mal. Se analizó uno de los productos y estaba mal. ¿Cuál es la probabilidad de que haya sido Andrés quien lo ha hecho?
Consideremos lo siguiente:
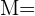 {Se hizo mal trabajo},
{Se hizo mal trabajo}, 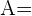 {El trabajo lo hizo Andrés},
{El trabajo lo hizo Andrés}, 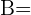 {El trabajo lo hizo Beto} y
{El trabajo lo hizo Beto} y 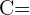 {El trabajo lo hizo Carlos}.
{El trabajo lo hizo Carlos}.
De estos sucesos se obtienen las probabilidades:
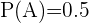 ,
, 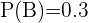 ,
, 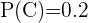 ,
, 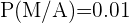 ,
, 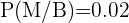 y
y 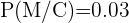 .
.
Usamos el teorema de Bayes para encontrar la probabilidad de que Andrés lo haya hecho mal
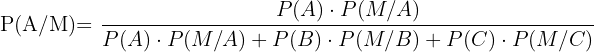
Sustituimos los valores y queda
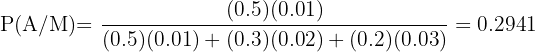
Propiedades
1 Propiedad que implica la probabilidad es no negativa y menor que 1. Esta propiedad indica que la probabilidad se maneja en el porcentaje del  % al
% al  % por lo tanto el
% por lo tanto el  % implica que no hay probabilidad, el
% implica que no hay probabilidad, el  % que se cumple la predicción y los valores intermedios te indica qué posibilidad hay de que se dé el suceso esperado.
% que se cumple la predicción y los valores intermedios te indica qué posibilidad hay de que se dé el suceso esperado.
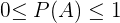
2 Propiedad de que es seguro que ocurra. Unn ejemplo para esta propiedad sería un dado con todas caras grabado el numero  , entonces la probabilidad de que cuando lo lances y salga un
, entonces la probabilidad de que cuando lo lances y salga un  es del
es del  %
%
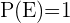
3 Propiedad es que es seguro no que ocurra. Para esta propiedad usamos el mismo dado del ejemplo anterior y lo lanzamos. ¿Cuál sería la probabilidad de salga un  ? La probabilidad sería nula pues solo está el número
? La probabilidad sería nula pues solo está el número  y por lo tanto la probabilidad sería
y por lo tanto la probabilidad sería  .
.
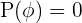
4 Propiedad de probabilidad del complemento de un suceso. Para esta propiedad supongamos que lanzamos un dado normal numerado del  al
al  y queremos saber la probabilidad de que no salga
y queremos saber la probabilidad de que no salga  , entonces llamamos
, entonces llamamos  al suceso de que salga
al suceso de que salga  ,
, 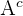 sería el suceso de que no salga
sería el suceso de que no salga  y
y 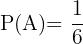 . Por lo tanto usamos la fórmula:
. Por lo tanto usamos la fórmula:
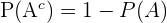
Sustituimos:
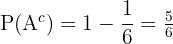 .
.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3