A continuación te presentamos una serie de ejercicios de combinaciones, esto es, agrupaciones
donde no importa el orden, los elementos se pueden o no repetir y no se consideran todos los elementos.
Comites distintos. En una clase de  alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
Primero, deberíamos notar lo siguiente:
No entran todos los elementos. Esto ya que solo se toman  de los
de los  alumnos.
alumnos.
No importa el orden. Esto ya que es lo mismo escoger a Juan, María y Cynthia que escoger a Cynthia a Juan y a Maria. Solo importa quiénes conforman el comité, no el orden como estos sean escogidos.
No se repiten los elementos. Esto ya que obviamente no podemos elegir más de una vez a una persona. Una vez que alguien es elegido, ya no pertenece al grupo de los alumnos restantes.
Dicho lo anterior, es claro que estamos frente a un problema que podemos resolver con combinaciones de la siguiente manera
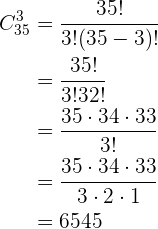
Colores del arcoiris. Dados los colores del arcoíris, ¿cuántos grupos de tres colores podemos formar con ellos?
Para resolver este problema primero debemos notar lo siguiente:
No entran todos los elementos. Esto ya que únicamente tomaremos  de los
de los  colores en el arcoíris.
colores en el arcoíris.
No importa el orden. Esto ya que solo nos importa los colores que escogemos pero no el orden en el que los escogemos.
No se repiten los elementos. Está claro que no podemos escoger más de una vez un color. Al tomar un color, este ya no se considera para la siguiente elección, podríamos decir que "lo sacamos del conjunto".
Dicho lo anterior es claro que este problema lo podemos resolver utilizando la fórmula de combinaciones:
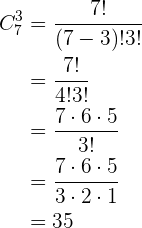
Numero de saludos en una reunión. A una reunión asisten  personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
Notemos lo siguiente:
No entran todos los elementos. Esto debido a que un saludo lo podemos analizar como un grupo de dos personas (ya que solo se efectúa entre dos personas).
No importa el orden. Esto ya que es lo mismo que Juan haya saludado a María a que María haya saludo a Juan.
No se repiten los elementos. Notemos que el asumir que se repiten es como pensar que una persona se pudo saludar a sí misma, esto no tendría sentido.
Dicho lo anterior, tenemos que este problema lo podemos resolver aplicando la fórmula de combinaciones:
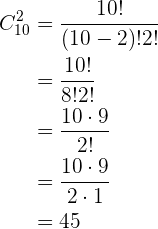
Combinaciones con botellas. En una tienda se venden cinco sabores distintos de refresco. Se desea comprar  , sin importar que se escojan varios del mismo sabor. ¿De cuántas formas se pueden elegir los sabores de refresco?
, sin importar que se escojan varios del mismo sabor. ¿De cuántas formas se pueden elegir los sabores de refresco?
Primero notemos los siguientes datos:
No entran todos los elementos. Esto debido a que hay cinco sabores y nosotros solo tomaremos  .
.
No importa el orden. Da igual que si se eligen dos refresco sabor cola y dos sabor manzana,
que primero dos sabor manzana y luego dos sabor cola.
Sí se repiten los elementos. Esto ya que podemos escoger los cuatro sabores diferentes o bien los cuatro iguales, etc.
Dicho lo anterior, es claro que tratamos con combinaciones con repetición, así, aplicando la fórmula, tenemos el resultado
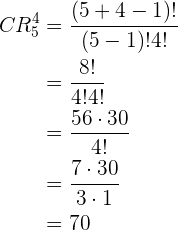
Combinaciones posibles en la lotería nacional. ¿Cuántas apuestas de Lotería Primitiva de una columna han de rellenarse para asegurarse el acierto de los seis resultados, de  ?
?
Primero notemos lo siguiente:
No entran todos los elementos. Esto ya que solo escogemos  de
de  elementos.
elementos.
No importa el orden. En este caso solo importa los elementos que escogamos pero no lo orden de estos.
No se repiten los elementos. Esto ya que no podemos escoger varias veces el mismo elemento de la loteria.
Dicho lo anterior, es claro que podemos resolver este problema aplicando la fórmula de combinaciones:
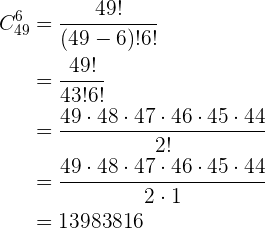
Cantidad de triángulos en un pentágono. ¿Cuántas diagonales tiene un pentágono y cuántos triángulos se pueden formar con sus vértices?
Primero necesitamos determinar las rectas que se pueden trazar entre 2 vértices. Notemos que tenemos 5 vértice y cada recta se puede determinar como el par de vértices que la definen, por lo tanto, tendríamos combinaciones.
No entran todos los elementos. Esto porque una recta solo la definen  de los
de los  vértices.
vértices.
No importa el orden. Una recta está definida porque une dos vértices, pero no hay dirección alguna, así que no importa qué vertice consideremos primero.
No se repiten los elementos. Esto porque considerar la repetición de elementos sería considerar rectas que van de un punto a sí mismo, esto no tendría sentido.
Así, tendríamos 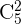 , a las que tenemos que restar los lados que determinan
, a las que tenemos que restar los lados que determinan  rectas
rectas
que no son diagonales.
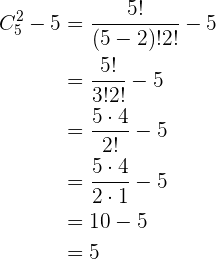
El número anterior no dio el número de diagonales dentro del pentágono. Ahora, cada tres diagonales cualesquiera define un triángulo dentro del pentágono, aunque no siempre el lado del triángulo será toda la diagonal, a veces solo serán parte de esta, esto lo podemos ver en el gráfico de cualquier pentágono con sus diagonales, podemos ver que sin importar cuales diagonales tomemos, entre estas se formará un triángulo, aunque solo esté definido por una parte de las diagonales. Dicho lo anterior, entonces cada triángulo lo define  de las
de las  diagonales, así, tenemos de nuevo combinaciones ya que
diagonales, así, tenemos de nuevo combinaciones ya que
No entran todos los elementos. Esto porque una recta solo la definen  de las
de las  diagonales.
diagonales.
No importa el orden. Un triángulo está definido por  diagonales sin importar el orden en que tomes estas.
diagonales sin importar el orden en que tomes estas.
No se repiten los elementos. Esto porque los tres lados de un triángulo siempre son segmentos de recta diferentes.
Así, tendríamos  .
.
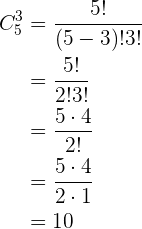
Combinaciones con condiciones. Un grupo, compuesto por cinco hombres y siete mujeres, forma un comité de 2 hombres y 3 mujeres. De cuántas formas puede formarse, si
1 Puede pertenecer a él cualquier hombre o mujer.
2 Una mujer determinada debe pertenecer al comité.
3 Dos hombres determinados no pueden estar en el comité.
1 Puede pertenecer a él cualquier hombre o mujer.
Notemos que como se puede escoger a cualquier hombre, entonces podemos escoger a cualesquiera  de los
de los  hombres. Igual, notemos que se cumplen las condiciones del ejercicio 1:
hombres. Igual, notemos que se cumplen las condiciones del ejercicio 1:
No entran todos los elementos. Esto ya que solo se toman  de los
de los  hombres.
hombres.
No importa el orden. Esto ya que es lo mismo escoger a Juan y Pedro que escoger a Pedro y a Juan.
No se repiten los elementos. Esto ya que obviamente no podemos elegir más de una vez a una persona..
Esto nos darían combinaciones de 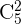 para poder escoger a los dos hombres. Al igual, podemos escoger entre todas las mujeres y, además, se cumplen las mismas condiciones, por lo tanto serían combinaciones
para poder escoger a los dos hombres. Al igual, podemos escoger entre todas las mujeres y, además, se cumplen las mismas condiciones, por lo tanto serían combinaciones 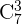 formas distintas de tomar
formas distintas de tomar  de las
de las  mujeres. Esto nos da como resultado final el producto de las combinaciones que obtuvimos. Esto es
mujeres. Esto nos da como resultado final el producto de las combinaciones que obtuvimos. Esto es
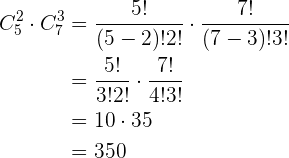
2 Una mujer determinada debe pertenecer al comité.
Notemos que al igual que en el inciso anterior, podemos escoger entre todos los hombres, por lo tanto de nuevo tendríamos combinaciones 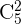 en los hombres. Ahora, a diferencia del inciso anterior con las mujeres, aquí nos dice que una mujer ya está determinada, o sea, ya es eleginada, por lo tanto, ahora debemos elegir las
en los hombres. Ahora, a diferencia del inciso anterior con las mujeres, aquí nos dice que una mujer ya está determinada, o sea, ya es eleginada, por lo tanto, ahora debemos elegir las  que faltan entre las
que faltan entre las  restantes, esto lo calculamos con las combinaciones
restantes, esto lo calculamos con las combinaciones  . Así, de nuevo nuestro resultado final es el producto de nuestras combinaciones obtenidas:
. Así, de nuevo nuestro resultado final es el producto de nuestras combinaciones obtenidas:
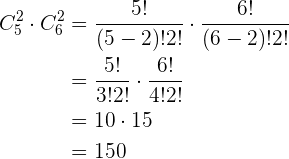
3 Dos hombres determinados no pueden estar en el comité.
Notemos que al igual que en el inciso 1, podemos escoger entre todos las mujeres, por lo tanto de nuevo tendríamos combinaciones 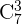 en los mujeres. Ahora, a diferencia de los incisos anteriores, aquí nos dicen que dos hombres de los
en los mujeres. Ahora, a diferencia de los incisos anteriores, aquí nos dicen que dos hombres de los  no pueden se escogidos, por lo tanto, tenemos que escoger a los
no pueden se escogidos, por lo tanto, tenemos que escoger a los  entre los
entre los  restantes, esto lo calculamos con las combinaciones
restantes, esto lo calculamos con las combinaciones 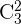 . Por último, nuestro resultado final está dado por el producto de las combinaciones obtenidas
. Por último, nuestro resultado final está dado por el producto de las combinaciones obtenidas
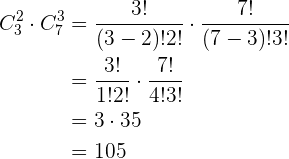
Combinaciones con monedas. Una persona tiene cinco monedas de distintos valores. ¿Cuántas sumas diferentes de dinero puede formar con las cinco monedas?
Notemos que es una pregunta un poco engañosa. Aquí se nos pide calcular las diferentes sumas, de lo cual uno podría cometer el error de las diferentes sumas al tomar todas las monedas (las cinco monedas), sin embargo, lo que debemos considerar son las diferentes sumas tomar sólo una moneda, al tomar dos monedas, tres monedas, cuadro monedas y cinco monedas, cuyos distintas sumas están dadas por 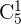 ,
, 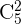 ,
,  ,
, 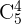 y
y  , respectivamente. Esto es, debemos sumar las distintas maneras de formar grupos de una moneda, grupos de dos monedas, de tres monedas y así sucesivamente.
, respectivamente. Esto es, debemos sumar las distintas maneras de formar grupos de una moneda, grupos de dos monedas, de tres monedas y así sucesivamente.
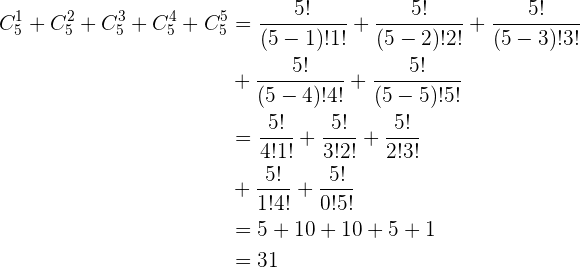
Ecuaciones de combinatorias. Resolver las siguientes ecuaciones combinatorias:
1
2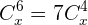
3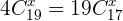
1
Resolveremos utilizando simplemente las definiciones de variaciones y de combinaciones
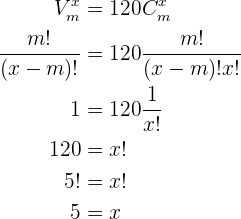
Por lo tanto  .
.
2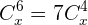
Nuevamente utilizaremos la definición de combinaciones para resolver este problema
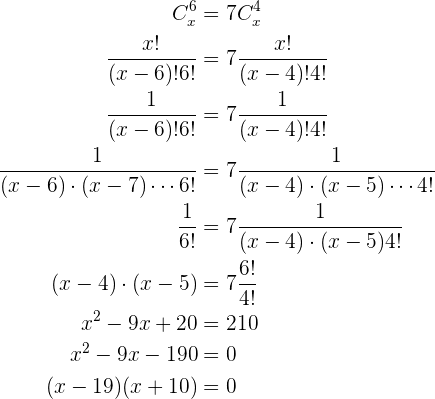
De lo anterior se sigue que 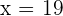 o
o 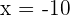 , sin embargo, como
, sin embargo, como  debe ser obligatoriamente positivo, tenemos que nuestra única opción es
debe ser obligatoriamente positivo, tenemos que nuestra única opción es 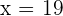 .
.
3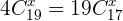
Nuevamente utilizaremos la definición de combinaciones para resolver este problema
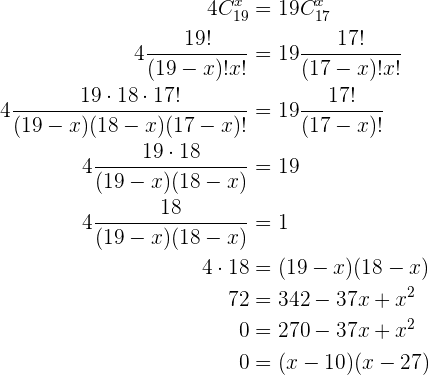
De lo anterior se sigue que 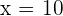 o
o 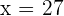 , sin embargo, como
, sin embargo, como  debe ser obligatoriamente menor a
debe ser obligatoriamente menor a  y
y  , ya que no podemos tomar más elementos de los que hay en un conjunto, tenemos que nuestra única opción es
, ya que no podemos tomar más elementos de los que hay en un conjunto, tenemos que nuestra única opción es 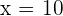 .
.
Combinaciones para formar equipos. A partir de  personas, ¿cuántos equipos diferentes se puede formar?
personas, ¿cuántos equipos diferentes se puede formar?
Como en este problema no se indica la cantidad de personas en el equipo, debemos considerar los diferentes equipos integrados por sólo una persona, dos personas, tres personas, cuadro personas, cinco personas y seis personas, cuyos distintas sumas están dadas por 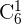 ,
, 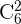 ,
, 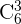 ,
, 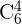 ,
,  y
y 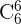 , respectivamente. Esto es, debemos sumar las distintas maneras de formar grupos de una persona, grupos de dos personas, de tres personas y así sucesivamente.
, respectivamente. Esto es, debemos sumar las distintas maneras de formar grupos de una persona, grupos de dos personas, de tres personas y así sucesivamente.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El ejercicio 7 está mal ya que el 5% de la población enferma no le corresponde una probabilidad del 0,005 sino del 0,05
Hola tienes razón, 5% es 0,05 pero no encontré el ejercicio que mencionas, podrías dar mas detalles por favor.
Hay un error en el problema 18 en la solución a, ya que al tener 20 hombres solteros, la probabilidad deria de 20/120 y no de 25/120 como se afirma
Hola revise los artículos y no encontré el problema, podrías hacerme el favor de darme el nombre del artículo, nos seria de mucha ayuda.
Hola! Este ejercicio creo que está mal…
Un hombre es conocido por decir la verdad 2 de 3 veces. El tira una moneda y dice que ha caído cara. Encuentra la probabilidad de que en realidad la moneda haya caído cara.
No se está considerando que, cuando dice la verdad, las chances son del 100% de que sea cara. No hay posibilidad de que sea ceca porque sino estaría mintiendo.
Hola agradecemos tus comentarios, podrías mencionar que número de ejercicio es pues hice una revisión y no encontré el ejercicio, seria de mucha ayuda por favor.
Quiero aprender más sobre matemáticas 💯 y como puedo hacer un ejemplo sobre la clase de permutaciones…y que fórmulas debo usar
Hola estas en el lugar indicado para aprender matematicas, en cuanto al tema que mencionas tenemos varios artículos que te pueden ayudar por ejemplo «https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/combinatoria/variaciones-permutaciones-y-combinaciones.html» con este puedes comenzar.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.