Capítulos
Ecuaciones con término cuadrático igualado a cero
Ecuaciones de la forma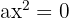 
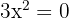
Para resolver tal ecuación vamos a utilizar simples despejes.
ahora pasamos el 3 dividiendo al otro miembro
,
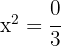luego, tenemos que
.
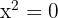Por lo tanto, la solución de la ecuación cuadrática es 0.
.
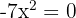
Para resolver tal ecuación vamos a utilizar simples despejes.
ahora pasamos el -7 dividiendo al otro miembro
,
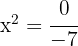luego, tenemos que
.
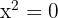Por lo tanto, la solución de la ecuación cuadrática es 0.
.
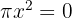
Para resolver tal ecuación vamos a utilizar simples despejes.
ahora pasamos el 
dividiendo al otro miembro
,
luego, tenemos que
.
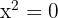Por lo tanto, la solución de la ecuación cuadrática es 0.
.
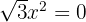
Para resolver tal ecuación vamos a utilizar simples despejes.
ahora pasamos el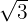 
dividiendo al otro miembro
,
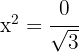luego, tenemos que
.
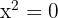Por lo tanto, la solución de la ecuación cuadrática es 0.
.
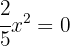
Para resolver tal ecuación vamos a utilizar simples despejes. Primero pasamos el 5 al otro miembro multiplicando, es decir,
,
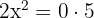así,
,
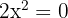ahora pasamos el 2 dividiendo al otro miembro
,
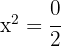luego, tenemos que
.
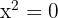Por lo tanto, la solución de la ecuación cuadrática es 0.
.
Ecuaciones con término cuadrático e independiente igualado a cero
Ecuaciones de la forma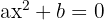 
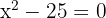
Para tal ecuación primero despejamos el término cuadrático, es decir,
,
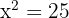ahora, sacamos raíz cuadrada de ambos lados
,
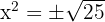así, obtenemos que las soluciones son:
.
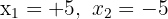Para tal ecuación primero despejamos el término cuadrático, es decir,
,
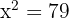ahora, sacamos raíz cuadrada de ambos lados
,
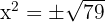así, obtenemos que las soluciones son:
.
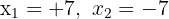Para tal ecuación primero despejamos el término cuadrático, es decir,
luego,
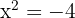
ahora sacamos raíz cuadrada de ambos lados
,
pero la raíz cuadrada de un número negativo en los números reales no existe, entonces la ecuación no tiene raíces reales.
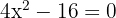
Despejar el término cuadrático, para obtener
,
sacamos la raíz cuadrada de ambos lados,
,
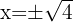y obtenemos que las soluciones son:
.
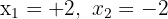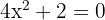
Despejar el término cuadrático, para obtener
,
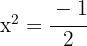sacamos la raíz cuadrada de ambos lados,
,
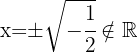pero la raíz cuadrada de un número negativo en los números reales no existe, entonces la ecuación no tiene raíces reales.
Ecuaciones con término cuadrático y lineal igualado a cero
Ecuaciones de la forma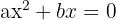 
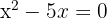
Para tal ecuación sacamos el factor común que es x, es decir,
,
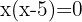como tenemos un producto igualado a cero, sucede que, o un factor es cero o el otro factor es cero o ambos son cero, así tenemos que,
,
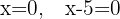por lo tanto, las soluciones para la ecuación dada son 0 y 5
.
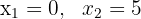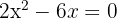
Para tal ecuación sacamos el factor común que es 2x, esto es,
,
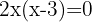como tenemos un producto igualado a cero, sucede que, o un factor es cero o el otro factor es cero o ambos son cero, así tenemos que,
,
por lo tanto, las soluciones para la ecuación dada son:
.
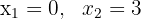Simplificamos la ecuación dividiendo por 3, obteniendo
,
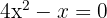sacamos el factor común x,
,
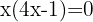como tenemos un producto igualado a cero, o un factor es cero o el otro factor es cero o ambos son cero
,
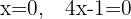entonces, las soluciones son:
.
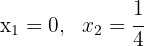Sacamos factor común 3x,
,
como tenemos un producto igualado a cero, sucede que, o un factor es cero o el otro factor es cero o ambos son cero, así tenemos que,
,
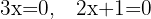entonces, las soluciones son:
.
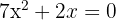
Sacamos factor común x,
,
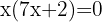como tenemos un producto igualado a cero, sucede que, o un factor es cero o el otro factor es cero o ambos son cero, así tenemos que,
,
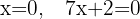entonces, las soluciones son:
.
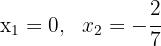Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Habéis cometido un error en el 2 de irracionales habéis puesto un 6 y es un 5
Una disculpa por que se brinca un paso pues el ejercicio es √x-1=5 y falto que √x=5+1, y aparece de repente √x=6.
Muy buenos ejercicios. Solamente una aclaración: en el problema 9 hay un error en la factorización del trinomio x2 – 28x + 169, los binomios serían: ( x – 21 )( x – 7 ) ; y no ( x – 21) ( x + 7 ). La ecuación tiene dos soluciones positivas, x = 21 y x = 21, pero la que da solución al problema es x = 21 por la condicionante «la edad que tenía hace 13 años»
Hola ya revise el ejercicio y la solución es (x-21)(x-7)=0, entonces los valores son x1=21, x=7, tal como lo indicas y no encontré el error que mencionas.
Factorización de un trinomio 2do grado
SRS. SUPERPROF.- CIENCIAS MATEMÁTICAS, REQUIERE DIFERENTES METODOLOGÍAS EN BIEN DE LOS EDUCANDOS. EL ESFUERZOS QUE VOSOTRO BRINDAN OBVIAMENTE ES EN BIEN DE NUESTRAS FUTURAS GENERACIONES. INFINITAS GRACIAS POR VUESTRAS HONORABLES DEDICACIONES. EN VERDAD, INFINITAS GRACIAS. DIOS LES ILUMINE POR SIEMPRE. BENDICIONES. AMEN.
Hola, con gusto te explicamos, podrías señalar cuales son las ecuaciones que no entiendes como se resolvieron y será un placer ayudarte.