Resuelve los siguientes problemas:
Sabemos que dos ciudades  y
y  distan
distan 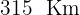 entre sí. Un coche sale de
entre sí. Un coche sale de  hacia
hacia  a una velocidad de
a una velocidad de  a las
a las  de la mañana. A la misma hora sale de
de la mañana. A la misma hora sale de  hacia
hacia  un camión. Suponiendo que ambos circulan a velocidad constante y sabiendo que se cruzan a las doce menos cuarto, ¿sabrías decir a qué velocidad circulaba el camión?
un camión. Suponiendo que ambos circulan a velocidad constante y sabiendo que se cruzan a las doce menos cuarto, ¿sabrías decir a qué velocidad circulaba el camión?
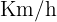
Este campo es obligatorio.
1 Sabemos que se cruzan a las  . Como salen a las
. Como salen a las 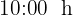 , en total tardan
, en total tardan 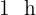 y
y 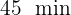 en cruzarse, es decir,
en cruzarse, es decir, 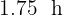
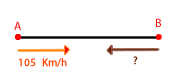
2 Sabemos que el espacio recorrido por el primer coche más el espacio recorrido por el segundo es igual a 
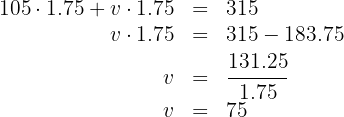
3 Así, el camión circulaba a
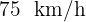
Dos ciudades  y
y  distan
distan  entre sí. Un coche parte de la ciudad
entre sí. Un coche parte de la ciudad  hacia la ciudad
hacia la ciudad  con una velocidad de
con una velocidad de 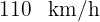 , y al mismo tiempo de la ciudad
, y al mismo tiempo de la ciudad  parte otro hacia la ciudad
parte otro hacia la ciudad  con una velocidad de
con una velocidad de  . Hallar el tiempo que tardarán en encontrarse.
. Hallar el tiempo que tardarán en encontrarse.

Este campo es obligatorio.
1 Sabemos que los autos salen al mismo tiempo de ambas ciudades, consideramos  el tiempo recorrido hasta el momento de cruzarse.
el tiempo recorrido hasta el momento de cruzarse.

2 Sabemos que el espacio recorrido por el primer coche más el espacio recorrido por el segundo es igual a 
 Así, ambos autos se cruzaran una hora después de iniciar su recorrido.
Así, ambos autos se cruzaran una hora después de iniciar su recorrido.
Dos puntos  y
y  están separados entres sí. Un ciclista parte de
están separados entres sí. Un ciclista parte de  hacia
hacia  con una velocidad de
con una velocidad de 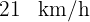 , y al mismo tiempo de
, y al mismo tiempo de  parte otro hacia
parte otro hacia  con una velocidad de
con una velocidad de  . Si se cruzan después de 15 minutos, hallar la distancia entre los dos puntos.
. Si se cruzan después de 15 minutos, hallar la distancia entre los dos puntos.

Este campo es obligatorio.
1 Sabemos que los ciclistas salen al mismo tiempo de ambos puntos y que tardan  desde el inicio hasta el momento de cruzarse.
desde el inicio hasta el momento de cruzarse.

2 Sabemos que el espacio recorrido por el primer ciclista más el espacio recorrido por el segundo es igual a la distancia entre los dos puntos
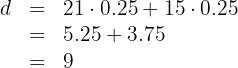 Así, ambos puntos se encuentran a
Así, ambos puntos se encuentran a 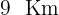 uno del otro.
uno del otro.
4A las  de la mañana Elena sale a
de la mañana Elena sale a 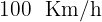 de una ciudad
de una ciudad  con dirección a Madrid. A la misma hora sale Javier desde otra ciudad
con dirección a Madrid. A la misma hora sale Javier desde otra ciudad  que situada en la misma dirección que
que situada en la misma dirección que  y lo hace a una velocidad de
y lo hace a una velocidad de 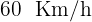 también con dirección a Madrid.
también con dirección a Madrid.
Sabiendo que la distancia en carretera entre  y
y  es de
es de 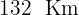 , y suponiendo que los dos van a una velocidad constante todo el camino, contesta a las siguientes preguntas:
, y suponiendo que los dos van a una velocidad constante todo el camino, contesta a las siguientes preguntas:
¿Qué tiempo tardarán en encontrarse Elena y Javier?
Tardarán 
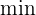
Este campo es obligatorio.
Sabemos que se encontrarán en un tiempo  . Como Javier lleva una ventaja de
. Como Javier lleva una ventaja de 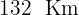 , tenemos
, tenemos
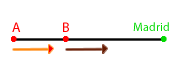
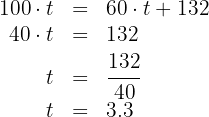
Así, Elena y Javier tardarán en encontrarse 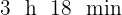 .
.
¿Qué hora será cuando se encuentren?
Serán las 
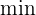
Este campo es obligatorio.
Sabemos que salen a las  , entonces la hora a la que se encotrarán es
, entonces la hora a la que se encotrarán es  s
s
¿Qué distancia habrá recorrido cada uno de ellos en ese momento?
Elena habrá recorrido  y Javier
y Javier 
Este campo es obligatorio.
La distancia que habrá recorrido Elena será 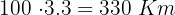
La distancia que habrá recorrido Javier será 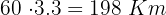
5Dos ciudades  y
y  distan
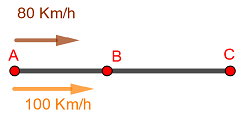
distan  entre sí. A las 10 de la mañana sale un coche de cada ciudad y los dos coches van en el mismo sentido.
entre sí. A las 10 de la mañana sale un coche de cada ciudad y los dos coches van en el mismo sentido.
El que sale de  circula a
circula a  , y el que sale de
, y el que sale de  va a
va a  y suponiendo que los dos van a una velocidad constante todo el camino, contesta a las siguientes preguntas:
y suponiendo que los dos van a una velocidad constante todo el camino, contesta a las siguientes preguntas:
¿Qué tiempo tardarán en encontrarse?
Tardarán 
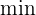
Este campo es obligatorio.
Sabemos que se encontrarán en un tiempo  . Como el segundo coche lleva una ventaja de
. Como el segundo coche lleva una ventaja de 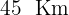 , tenemos
, tenemos

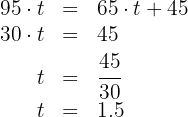
Así, ambos coches tardarán en encontrarse 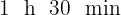 .
.
¿Qué hora será cuando se encuentren?
Serán las 
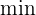
Este campo es obligatorio.
Sabemos que salen a las  , entonces la hora a la que se encotrarán es
, entonces la hora a la que se encotrarán es 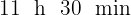 s
s
¿Qué distancia habrá recorrido cada uno de ellos en ese momento?
El coche que sale de  habrá recorrido
habrá recorrido  y el coche que sale de
y el coche que sale de 

Este campo es obligatorio.
La distancia que habrá recorrido el primer coche será 
La distancia que habrá recorrido el segundo coche será 
6Un ciclista parte de un punto  a una velocidad de
a una velocidad de 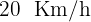 . Otro ciclista sale del mismo punto
. Otro ciclista sale del mismo punto  minutos más tarde. ¿Cuál deberá ser la velocidad de este segundo ciclista si pretende alcanzar al primero en una hora y cuarto?
minutos más tarde. ¿Cuál deberá ser la velocidad de este segundo ciclista si pretende alcanzar al primero en una hora y cuarto?
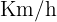
Este campo es obligatorio.
1 Llamamos 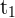 al tiempo que pedalea el primer ciclista y
al tiempo que pedalea el primer ciclista y 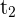 al tiempo que pedalea el segundo, entonces
al tiempo que pedalea el segundo, entonces


2 Si el segundo ciclista pretende alcanzar al primero en una hora y cuarto esto significa que el primer ciclista pedalea durante una hora y media. Entonces tenemos:
 De donde,
De donde, 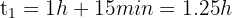
3 La distancia recorrida debe ser la misma por ambos ciclistas.
 La velocidad del segundo ciclista debe ser de
La velocidad del segundo ciclista debe ser de  .
.
7Un coche sale de la ciudad  con velocidad de
con velocidad de 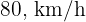 . Una hora más tarde sale de la misma ciudad otro coche en persecución del primero con una velocidad de
. Una hora más tarde sale de la misma ciudad otro coche en persecución del primero con una velocidad de  . ¿A qué distancia se produce el encuentro.
. ¿A qué distancia se produce el encuentro.

Este campo es obligatorio.
1 Si el tiempo empleado por el primer coche es 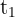 , el del segundo que sale una hora más tarde será
, el del segundo que sale una hora más tarde será

2 Sabemos que la distancia recorrida por ambos coches es la misma

3 Sustituimos 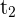
 La distancia a la que se encuentran ambos coches es
La distancia a la que se encuentran ambos coches es 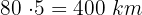 .
.
Si tienes dudas puedes consultar la teoría
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Habéis cometido un error en el 2 de irracionales habéis puesto un 6 y es un 5
Una disculpa por que se brinca un paso pues el ejercicio es √x-1=5 y falto que √x=5+1, y aparece de repente √x=6.
Muy buenos ejercicios. Solamente una aclaración: en el problema 9 hay un error en la factorización del trinomio x2 – 28x + 169, los binomios serían: ( x – 21 )( x – 7 ) ; y no ( x – 21) ( x + 7 ). La ecuación tiene dos soluciones positivas, x = 21 y x = 21, pero la que da solución al problema es x = 21 por la condicionante «la edad que tenía hace 13 años»
Hola ya revise el ejercicio y la solución es (x-21)(x-7)=0, entonces los valores son x1=21, x=7, tal como lo indicas y no encontré el error que mencionas.
Factorización de un trinomio 2do grado
SRS. SUPERPROF.- CIENCIAS MATEMÁTICAS, REQUIERE DIFERENTES METODOLOGÍAS EN BIEN DE LOS EDUCANDOS. EL ESFUERZOS QUE VOSOTRO BRINDAN OBVIAMENTE ES EN BIEN DE NUESTRAS FUTURAS GENERACIONES. INFINITAS GRACIAS POR VUESTRAS HONORABLES DEDICACIONES. EN VERDAD, INFINITAS GRACIAS. DIOS LES ILUMINE POR SIEMPRE. BENDICIONES. AMEN.
Hola, con gusto te explicamos, podrías señalar cuales son las ecuaciones que no entiendes como se resolvieron y será un placer ayudarte.