La ley de la aleación es la relación entre el peso del metal fino, es decir, más valioso, y el peso total. En una aleación siempre intervienen un metal fino o precioso y un metal ordinario también llamado liga
Se llama ley a la razón que existe entre el peso del metal fino y el peso total de la aleación. Matemáticamente la ley es
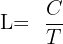
donde:
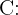Peso del metal fino
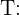Peso total de la aleación
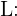Ley de la aleación
Problema 1:
¿Cuál es la ley de una aleación conformada por 
gramos de plata y 
gramos de níquel?
El peso total de la aleación es de
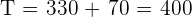
el peso del metal fino es
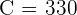
entonces la ley de aleacion seria
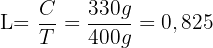
Es decir, la ley de esta aleación es de 0.825.
Ahora supongamos que queremos hacer una aleación con dos metales, A y B, cada uno con una ley de aleación distinta. En este caso tendremos la siguiente formula general:
donde
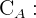cantidad del metal A
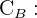cantidad del metal B
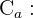cantidad total de la aleación, es decir,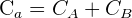 
ley de aleación del metal A
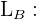ley de aleación del metal B
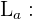ley de aleación del metal resultante
Por tanto, tendremos que la ley de aleación del metal resultante entre los dos es
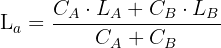
Problema 2:
Un lingote de plata de 
g de ley del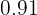 
(91 % de pureza) se funde con otro de 
g de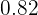 
de ley. ¿Cuál es la ley del nuevo lingote?
Estamos buscando 
y tenemos que
entonces
Problema 3:
Se tienen dos lingotes de plata, uno de ley 
y otro de ley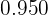 
. ¿Qué peso hay que tomar de cada lingote para obtener 
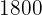g de plata de ley 
?
La cantidad total de aleación (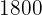 g) es la suma de ambos metales. Por tanto, si tenemos 
gramos de plata de tipo A, la cantidad de plata de tipo B será: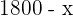 
. Y ahora con los datos que tenemos aplicamos la formula
entonces
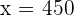
y de aquí
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Habéis cometido un error en el 2 de irracionales habéis puesto un 6 y es un 5
Una disculpa por que se brinca un paso pues el ejercicio es √x-1=5 y falto que √x=5+1, y aparece de repente √x=6.
Muy buenos ejercicios. Solamente una aclaración: en el problema 9 hay un error en la factorización del trinomio x2 – 28x + 169, los binomios serían: ( x – 21 )( x – 7 ) ; y no ( x – 21) ( x + 7 ). La ecuación tiene dos soluciones positivas, x = 21 y x = 21, pero la que da solución al problema es x = 21 por la condicionante «la edad que tenía hace 13 años»
Hola ya revise el ejercicio y la solución es (x-21)(x-7)=0, entonces los valores son x1=21, x=7, tal como lo indicas y no encontré el error que mencionas.
Factorización de un trinomio 2do grado
SRS. SUPERPROF.- CIENCIAS MATEMÁTICAS, REQUIERE DIFERENTES METODOLOGÍAS EN BIEN DE LOS EDUCANDOS. EL ESFUERZOS QUE VOSOTRO BRINDAN OBVIAMENTE ES EN BIEN DE NUESTRAS FUTURAS GENERACIONES. INFINITAS GRACIAS POR VUESTRAS HONORABLES DEDICACIONES. EN VERDAD, INFINITAS GRACIAS. DIOS LES ILUMINE POR SIEMPRE. BENDICIONES. AMEN.
Hola, con gusto te explicamos, podrías señalar cuales son las ecuaciones que no entiendes como se resolvieron y será un placer ayudarte.