Ejercicios propuestos
¿Necesitas clases particulares matematicas?
Un reloj marca las 3 en punto. ¿A qué hora entre las 3 y las 4 se superpondrán las agujas?
x es el arco que describe la aguja horaria.
(15 + x) es el arco que describe el minutero.
El ángulo o arco descrito que recorre el minutero es siempre 12 veces mayor que el arco que describe la aguja horaria
15 + x = 12x
x = 15/11 min = 1.36 min − 1min = 0.36
Los 0.36 minutos los multiplicamos por 60 y obtenemos 21 segundos
Las agujas se superpondrán un minuto y 21 segundo después de la tres y cuarto: 3 h 16 min 21 s
Un reloj marca las 2 en punto. ¿A qué hora formarán sus agujas por primera vez un ángulo recto?
Las agujas del reloj forman un ángulo recto a las 2 h 25 min y un poco más, que llamaremos x.
x es el arco que describe la aguja horaria.
25 + x, es el arco que describe el minutero.
El ángulo o arco descrito que recorre el minutero es siempre 12 veces mayor que el arco que describe la aguja horaria
25 + x = 12x
x = 25/11 min = 2.27 min − 2 min = 0.27
Los 0.27 minutos los multiplicamos por 60 y obtenemos 16 segundos
Las agujas se superpondrán 2 minutos y 21 segundo después de la 2 h 25 min: 2h 27 min 16 s
Dos ciudades A y B distan 300 km entre sí. A las 9 de la mañana parte de la ciudad A un coche hacia la ciudad B con una velocidad de 90 km/h, y de la ciudad B parte otro hacia la ciudad A con una velocidad de 60 km/h. Se pide:
a El tiempo que tardarán en encontrarse.
El espacio es igual a la velocidad por el tiempo, por tanto el espacio recorrido por el primero será 90t y el espacio recorrido por el segundo es 60t
Sabemos que el espacio recorrido por el primero más el espacio recorrido por el segundo es igual a 300 Km
90t + 60t = 300 150t = 300 t = 2 horas
b La hora del encuentro.
Se encontraran a las 11 de la mañana porque parten a las 9 de la mañana y transcurren dos horas hasta el encuentro.
c La distancia recorrida por cada uno.
e AB = 90 · 2 = 180 km
e BC = 60 · 2 = 120 km
Dos ciudades A y B distan 180 km entre sí. A las 9 de la mañana sale de un coche de cada ciudad y los dos coches van en el mismo sentido. El que sale de A circula a 90 km/h, y el que sale de B va a 60 km/h. Se pide:
a El tiempo que tardarán en encontrarse.
El espacio es igual a la velocidad por el tiempo, por tanto el espacio recorrido por el primero será 90t y el espacio recorrido por el segundo es 60t
El espacio recorrido por el primero menos el espacio recorrido por el segundo es igual a 180 Km
90t − 60t = 180 30t = 180 t = 6 horas
b La hora del encuentro.
Se encontraran a las 3 de la arde porque parten a las 9 de la mañana y transcurren seis horas hasta el encuentro.
c La distancia recorrida por cada uno.
eAB = 90 · 6 = 540 km
eBC = 60 · 6 = 360 km
Un coche sale de la ciudad A a la velocidad de 90 km/h. Tres horas más tarde sale de la misma ciudad otro coche en persecución del primero con una velocidad de 120 km/h. Se pide:
a El tiempo que tardará en alcanzarlo.
Si el tiempo empleado por el primero es t, el del segundo que sale tres horas más tarde será t − 3
El espacio es igual a la velocidad por el tiempo, por tanto el espacio recorrido por el primero será 90t y el espacio recorrido por el segundo es 120(t − 3)
90t = 120 · (t − 3)
90t = 120t − 360 −30t = −360 t = 12 horas
El primer coche tarda 12 h.
El segundo coche tarda (12 − 3) = 9 h.
b La distancia a la que se produce el encuentro.
Calculamos el espacio recorrido por uno de los dos
e1 = 90 · 12 = 1080 km
Un camión sale de una ciudad a una velocidad de 40 km/h. Una hora más tarde sale de la misma ciudad y en la misma dirección y sentido un coche a 60 km/h. Se pide:
a Tiempo que tardará en alcanzarle.
e1 = e2
Si el tiempo empleado por el primero es t, el del segundo que sale una hora más tarde será t − 1
El espacio es igual a la velocidad por el tiempo, por tanto el espacio recorrido por el primero será 40t y el espacio recorrido por el segundo es 60(t − 1)
40t = 60 (t − 1)
40t = 60t − 60 40t − 60t = −60 −20t = −60
t = 3h
Como el coche sale una hora más tarde, el tiempo que tardará en alcanzarlo será de 2 horas.
b Distancia al punto de encuentro.
Calculamos el espacio recorrido por uno de los dos
e1 = 40 · 3 = 120 km .
Dos ciclistas salen en sentido contrario a las 9 de la mañana de los pueblos A y B situados a 130 kilómetros de distancia. El ciclista que sale de A pedalea a una velocidad constante de 30 km/h, y el ciclista que sale de B, a 20 km/h. ¿A qué distancia de A se encontrarán y a qué hora?
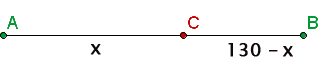
El espacio es igual a la velocidad por el tiempo, por tanto el espacio recorrido por el primero será 30t y el espacio recorrido por el segundo es 20t
Sabemos que el espacio recorrido por el primero más el espacio recorrido por el segundo es igual a 130 Km
30t + 20t = 130 50t = 130
t = 130/50 = 2 h 36 min
Se encontraran a las 11h 36 min de la mañana porque parten a las 9 de la mañana y transcurren 2 h 36 min hasta el encuentro.
e AC = 30 · 130/50 = 78 km
Un grifo tarda en llenar un depósito tres horas y otro grifo tarda en llenarlo cuatro horas. ¿Cuánto tiempo tardarán en llenar los dos grifos juntos el depósito?
En una hora el primer grifo llena 1/3 del depósito.
En una hora el segundo grifo llena 1/4 del depósito.
En una hora los dos grifos juntos habrán llenado:
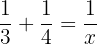
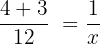
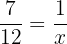
7x = 12 x = 12/7 horas
Un comerciante tiene dos clases de café, la primera a 40 € el kg y la segunda a 60 € el kg. ¿Cuantos kilogramos hay que poner de cada clase de café para obtener 60 kilos de mezcla a 50 € el kg?
| 1ª clase | 2ª clase | Total | |
|---|---|---|---|
| Nº de kg | x | 60 − x | 60 |
| Valor | 40 · x | 60 · (60 − x) | 60 · 50 |
Los kg del primer café por su precio más los kg del 2º café por su precio es igual al total de los kg de café multiplicado por el precio de la mezcla
40x + 60 · (60 − x) = 60 · 50
40x + 3600 − 60x = 3000; − 60x + 40x = 3000 − 3600; 20x = 600
x = 30; 60 − 30 = 30
Tenemos que mezclar 30 kg de la 1ª clase y otros 30 de la 2ª clase .
Se tienen dos lingotes de plata, uno de ley 0.750 y otro de ley 0.950. ¿Qué peso hay que tomar de cada lingote para obtener 1800 g de plata de ley 0.900?
| 1ª ley | 2ª ley | Total | |
|---|---|---|---|
| Nº de g | x | 1800 − x | 1800 |
| Plata | 0.750 · x | 0.950 · (1800−x) | 0.900 · 1800 |
0.750 · x + 0.950 · (1800 − x) = 0.9 · 1800
0.750x + 1710 − 0.950x = 1 620
0.750x − 0.950x = 1620 − 1710
−0.2x = − 90 x = 450
1ª ley 450 g
2ª ley 1350 g
Un lingote de oro de ley 0.950 pesa 6 300 g. ¿Qué cantidad de cobre puro se habrá de añadir para rebajar su ley a 0.900?
| Oro | Cobre | Total | |
|---|---|---|---|
| Nº de g | 6 300 | x | 6 300 + x |
| Oro puro | 0.950 · 6 300 | 0.900 · (6 300 + x) |
0.900 · (6 300 + x) = 0.950 · 6 300
5 670 + 0.900x = 5 985
0.900x = 315 x = 315/0.900 = 350
Cobre 350 g
Si vives en la capital y buscas un profesor particular matematicas madrid, ¡encuéntralo en Superprof!
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Factorización de un trinomio 2do grado
SRS. SUPERPROF.- CIENCIAS MATEMÁTICAS, REQUIERE DIFERENTES METODOLOGÍAS EN BIEN DE LOS EDUCANDOS. EL ESFUERZOS QUE VOSOTRO BRINDAN OBVIAMENTE ES EN BIEN DE NUESTRAS FUTURAS GENERACIONES. INFINITAS GRACIAS POR VUESTRAS HONORABLES DEDICACIONES. EN VERDAD, INFINITAS GRACIAS. DIOS LES ILUMINE POR SIEMPRE. BENDICIONES. AMEN.
2x+y-z=-1
X-2y+z=5
3x-y-2z=0
Me encuentro realizando los ejercicios de la pagina con mi hija a la cual le estoy explicando los metodos de resolucion geometricos y me encuentro con que dos de los ejercicios se los han calificado mal, las respuestas que tenemos son las misma ella y yo pues siguio los metodos paso a paso, pero nos encontramos con que el primer ejercicio califica la respuesta al reves y el segundo se la califica mal por no redondear el decimal… el segundo punto podria ser mas comprensible, pero el primero trajo a mi niña trantando de entender por que estaba mal durante 15 minutos hasta que vio que se le evaluava con los resultados cambiados, si el orden de los resultados importa para calificarlos, sean mas claros con donde los quieres pues el problema dice que el largo de un area es el triple del ancho del otro lado, en el largo pusimos la respuesta que es 3X = 131.25 y en ancho pusimos x que es 43.75, pues la pagina lo reviso como erroneo punoniendo que las cajas o las etiquetas del archivo html estan mal asignadas
Una disculpa ya se corrigió.
Y con a>1?
Hola podrías hacernos el favor de dar mas información como el número de ejercicio para poder resolver tu duda.
2x+y-z=-1
X-2y+z=5
3x-y-2z=0
Ecuaciones metodo Guss jordan
Hola soy David quisiera que me expliquen como se realizan las ecuaciones de 1er grado