¡Bienvenidos a nuestra página dedicada a ejercicios y problemas de ecuaciones de primer grado! Aquí, exploraremos cómo las ecuaciones lineales pueden ser la clave para resolver una variedad de problemas cotidianos. Desde calcular dimensiones de lugares hasta calcular razones, distancias y edades, las ecuaciones de primer grado están en todas partes.

En este espacio, aprenderás cómo traducir situaciones de la vida real en ecuaciones simples y luego resolverlas de manera efectiva. Nuestro objetivo es mostrarte cómo las matemáticas son mucho más que números en una página; son herramientas poderosas que pueden ayudarte a tomar decisiones informadas y resolver problemas en tu vida diaria. ¡Únete a nosotros en este viaje mientras descubrimos cómo las ecuaciones de primer grado pueden hacer que la vida sea más simple y más emocionante al mismo tiempo!

1

1Un padre tiene 35 años y su hijo 5. ¿Al cabo de cuántos años será la edad del padre tres veces mayor que la edad del hijo?

Solución

1Edad del hijo dentro de años :

2Edad del padre dentro de años:

3La edad del padre es igual al triple de la edad del hijo dentro de años

4Quitamos paréntesis

5Agrupamos términos y despejamos dividiendo por 2

6La respuesta es: al cabo de 10 años.

2

2Si al doble de un número se le resta su mitad resulta 54. ¿Cuál es el número?

Solución

1Número:

2Doble del número:

3Mitad del número:

4Si al doble del número le restamos la mitad obtenemos 54

5Quitamos denominadores, agrupamos términos y despejamos

6El número buscado es: 36

3

3La base de un rectángulo es el doble de su altura. ¿Cuáles son sus dimensiones si el perímetro mide 30 cm?

Solución

1Altura:

2Base:

3El perímetro de un rectángulo es la suma del doble de la altura más el doble de la base

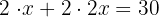
4Sumamos y despejamos

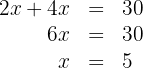
5La altura buscada es: 5 cm

La base buscada es: 10 cm

4

4En una reunión hay doble número de mujeres que de hombres y triple número de niños que de hombres y mujeres juntos. ¿Cuántos hombres, mujeres y niños hay si la reunión la componen 96 personas?

Solución

1Hombres

2Mujeres

3Niños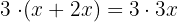

4En total hay 96

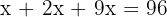
5Sumamos y despejamos

6Hombres: 8

Mujeres: 16

Niños: 72

5

5Se han consumido 7/8 de un bidón de aceite.   Reponemos 38 l y el bidón ha quedado lleno hasta sus 3/5 partes.   Calcula la capacidad del bidón.

Solución

1Llamamos a la capacidad del bidón y como hemos consumido 7/8 de su capacidad quedará:

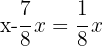
2Si reponemos 38 l se llenan 3/5 partes de capacidad del bidón

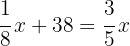
3Quitamos denominadores, el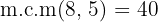

4Agrupamos términos y despejamos

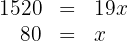
5La capacidad del bidón es: 80 l

6

6Una granja tiene cerdos y pavos, en total hay 35 cabezas y 116 patas. ¿Cuántos cerdos y pavos hay?

Solución

1Cerdos

2Pavos

3El total de patas será el cuádruple del número de cerdos más el doble del número de pavos.

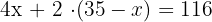
4Quitamos paréntesis

5Agrupamos y despejamos

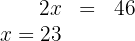
6Cerdos: 23

Pavos: 35 - 23 = 12

7

7Luis hizo un viaje en el coche, en el cual consumió 20 l de gasolina. El trayecto lo hizo en dos etapas: en la primera, consumió 2/3 de la gasolina que tenía el depósito y en la segunda etapa, la mitad de la gasolina que le queda. ¿Cuántos litros de gasolina tenía el depósito y cuánto consumió en cada etapa?

Solución

1 Litros de gasolina que tenía en el depósito:

Primera etapa

Segunda etapa

2Entre las dos etapas ha consumido 20 l

3Quitamos denominadores, sumamos y despejamos

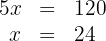
4Los resultados buscados son:

Cantidad en el depósito: 24 l

Cantidad consumida en la primera etapa: 16 l

Cantidad consumida en la segunda etapa: 4 l

8

8En una librería, Ana compra un libro con la tercera parte de su dinero y un cómic con las dos terceras partes de lo que le quedaba. Al salir de la librería tenía 12 €. ¿Cuánto dinero tenía Ana?

Solución

1Total

Libro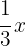

Cómic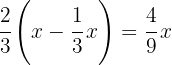

2El dinero que cuesta el libro, más el del cómic, más el dinero que le sobró será igual al dinero que tenía

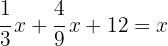
3Quitamos denominadores

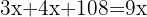
4Agrupamos términos y despejamos

5Ana tenía 24 €

9

9La dos cifras de un número son consecutivas. La mayor es la de las decenas y la menor la de las unidades. El número es igual a seis veces la suma de las cifras. ¿Cuál es el número?

Solución

1Unidades

Decenas

2Si tenemos un número de dos cifras, por ejemplo 65 podemos descomponerlo, de este modo: 6 · 10 + 5.

3Nuestro número de dos cifras es: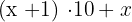

4Como este número es seis veces mayor que la suma de sus cifras: , tendremos:

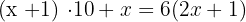
5Quitamos paréntesis y resolvemos

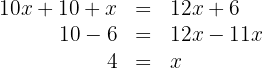
6Los resultados son:

Unidades: 4

Decenas: 5

Número: 54

10

10Las tres cuartas partes de la edad del padre de Juan excede en 15 años a la edad de éste. Hace cuatro años la edad de la padre era doble de la edad del hijo. Hallar las edades de ambos.

Solución

1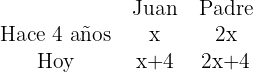

2Planteamos el problema

3Quitamos paréntesis, agrupamos términos y despejamos

4Las edades son: Juan: 32 + 4 = 36. Padre: 2 · 32 + 4 = 68

11

11Trabajando juntos, dos obreros tardan en hacer un trabajo 14 horas. ¿Cuánto tiempo tardarán en hacerlo por separado si uno es el doble de rápido que el otro?

Solución

1

2Planteamos el problema

2Calculamos el m.c.m. para poder quitar denominadores

3Multiplicamos ambos lados y resolvemos

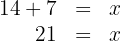
4Los resultados son:

Rápido: 21 horas

Lento 42 horas

12

12Halla el valor de los tres ángulos de un triángulo sabiendo que B mide 40° más que C y que A mide 40° más que B.

Solución

1C:

B: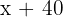

A: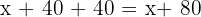

2La suma de los ángulos de un triángulo es igual a 180º

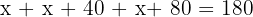
3Agrupamos términos

4Sumamos y despejamos

5Los ángulos son:

C = 20º, B = 20º + 40º = 60º,  A = 60º + 40º = 100º

13

13Un terreno tiene dimensiones de 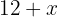metros de largo y 11 metros de ancho. Si su área es de 220 metros cuadrados, determina el valor de .

Solución

1Largo del terreno :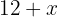

2Ancho del terreno:

3El área del terrreno es 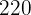metros cuadrados:

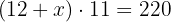
4Quitamos paréntesis

5Despejamos para

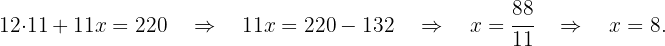
6La respuesta es: .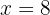

14

14Si a diez veces un número se le resta dos tercios del mismo resulta 56, ¿cuál es ese número?

Solución

1Número:

2Si a diez veces el número:

3Dos tercios del número: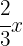

4Diez veces un número se le resta dos tercios del mismo resulta 56:

5Resolvemos para :

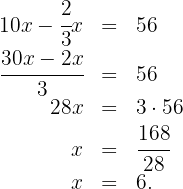
6La respuesta es: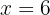

15

15Dos quintas partes de una manguera de riego equivalen a 60 metros. ¿Cuánto mide la manguera completa?

Solución

1Longitud de la manguera:

2Dos quientas partes de la manguera equivalen a 60 metros: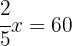

3Despejamos la ecuación para :

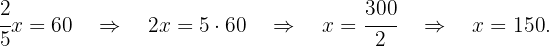
4La longitud de la manguera es metros.

En Superprof contamos con los mejores cursos de matematicas para ayudarte con todas tus dudas.

¿Te ha gustado este artículo? ¡Califícalo!

4,00 (683 nota(s))
Cargando...

Marta

➗ Licenciada en Químicas da clase de Matemáticas, Física y Química -> Comparto aquí mi pasión por las matemáticas ➗