Bienvenidos a nuestra sección dedicada a la resolución de Ecuaciones Lineales y su aplicación en una amplia variedad de problemas. Las ecuaciones lineales son la base de las matemáticas y tienen una amplia gama de aplicaciones en diversos campos, desde la física hasta la economía. En esta guía, los acompañaremos en un viaje de aprendizaje que abarca tanto la resolución de ecuaciones lineales como su aplicación en situaciones del mundo real.
La resolución de una ecuación lineal implica encontrar el valor o los valores de una variable desconocida que hacen que la ecuación sea verdadera. Es un proceso sistemático que involucra manipulación algebraica cuidadosa. Además, aprenderemos a aplicar ecuaciones lineales para resolver problemas prácticos en diversas disciplinas.
Es fundamental recordar que el conocimiento y la aplicación de las ecuaciones lineales son habilidades esenciales en matemáticas y en la resolución de problemas cotidianos. A lo largo de esta guía, exploraremos ejercicios que nos ayudarán a comprender cómo utilizar esta herramienta matemática para analizar y resolver situaciones que podemos encontrarnos en nuestro día a día.

Ejercicios de ecuaciones
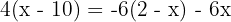
1Realizamos las multiplicaciones en ambos lados de la ecuación

2Sumamos y restamos términos semejantes en ambos lados de la ecuación
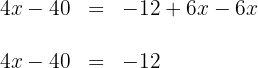
3Para despejar  , primero sumamos
, primero sumamos  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos
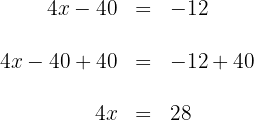
4Para obtener  , ahora multiplicamos por
, ahora multiplicamos por  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos
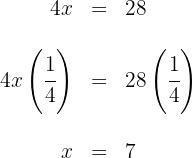
Así,  es la solución de la ecuación
es la solución de la ecuación

1Realizamos las multiplicaciones
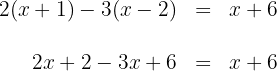
2Sumamos y restamos términos semejantes en ambos lados de la ecuación
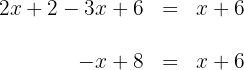
3Para despejar  , primero restamos
, primero restamos  y
y  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos
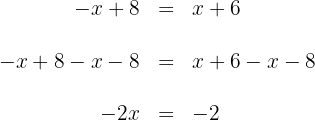
4Para obtener  , ahora multiplicamos por
, ahora multiplicamos por  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos

Así,  es la solución de la ecuación
es la solución de la ecuación
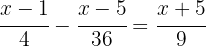
1Calculamos el 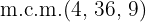
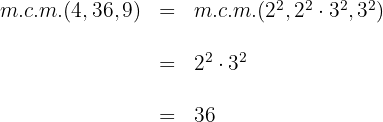
2Multiplicamos ambos lados de la ecuación por el 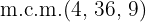
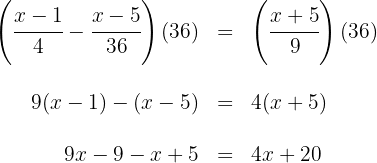
3Sumamos y restamos términos semejantes en ambos lados de la ecuación
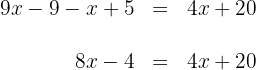
4Para despejar  , primero restamos
, primero restamos  y sumamos
y sumamos  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos
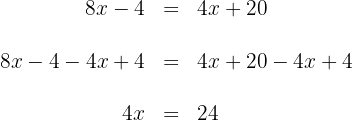
5Para obtener  , ahora multiplicamos por
, ahora multiplicamos por  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos
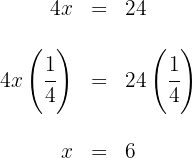
Así,  es la solución de la ecuación
es la solución de la ecuación
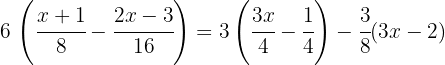
1Realizamos las multiplicaciones y simplificamos las fracciones
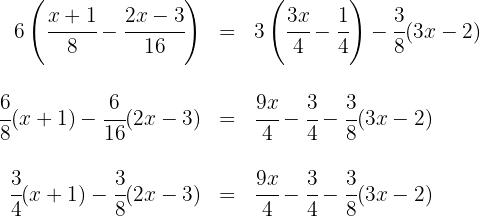
2Calculamos el 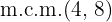 de los denominadores
de los denominadores
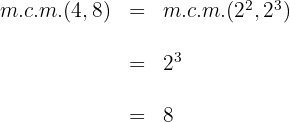
3Multiplicamos ambos lados de la ecuación por el 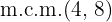
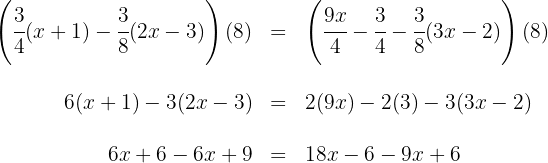
4Sumamos y restamos términos semejantes en ambos lados de la ecuación
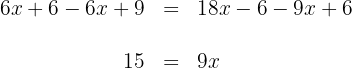
5Para despejar  , multiplicamos por
, multiplicamos por  en ambos lados de la ecuación y simplificamos
en ambos lados de la ecuación y simplificamos
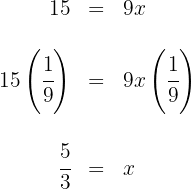
Así,  es la solución de la ecuación
es la solución de la ecuación

1Multiplicamos ambos lados de la ecuación por  y
y  y simplificamos
y simplificamos
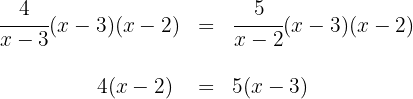
2Realizamos las multiplicaciones

3Restamos  y sumamos
y sumamos  en ambos lados de la ecuación
en ambos lados de la ecuación
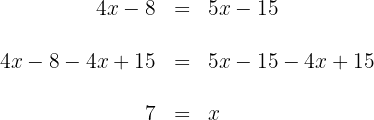
Así,  es la solución de la ecuación
es la solución de la ecuación
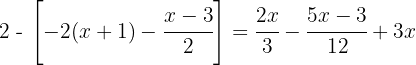
1Quitamos los corchetes

2Calculamos el  de los denominadores
de los denominadores

3Multiplicamos por el  ambos lados de la ecuación
ambos lados de la ecuación

4Sumamos y restamos términos semejantes
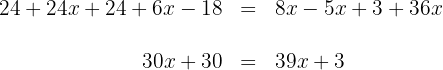
5Restamos 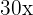 y
y  en ambos lados de la ecuación
en ambos lados de la ecuación
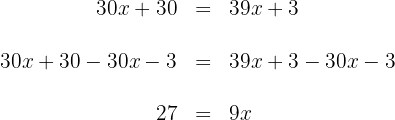
6Multiplicamos ambos lados de la ecuación por 

Así,  es la solución de la ecuación
es la solución de la ecuación
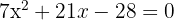
1Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
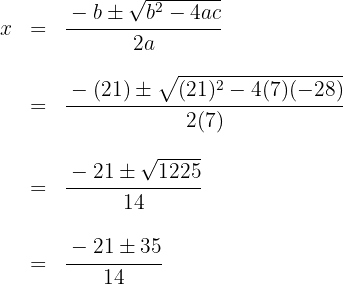
Las raíces son
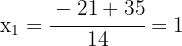
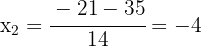
2Las raíces de la ecuación son las soluciones de la misma. Así, las soluciones buscadas son  y
y 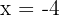

1Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado

Como en los reales no existen raíces de números negativos, concluimos que la ecuación no tiene soluciones reales.

1Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
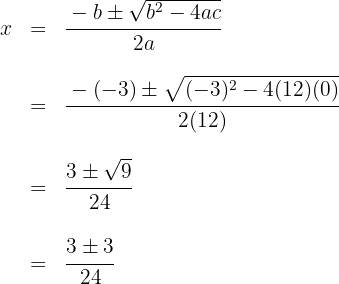
Las raíces son
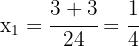
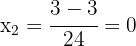
2Las raíces de la ecuación son las soluciones de la misma. Así, las soluciones buscadas son  y
y 
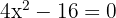
1Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
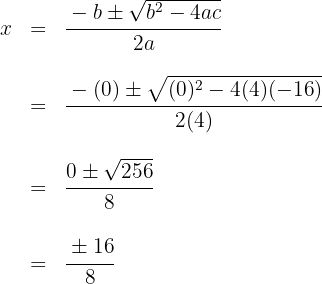
Las raíces son
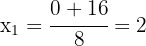
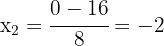
2Las raíces de la ecuación son las soluciones de la misma. Así, las soluciones buscadas son  y
y 
Problemas de aplicación
Un padre tiene 35 años y su hijo 5. ¿Al cabo de cuántos años será la edad del padre tres veces mayor que la edad del hijo?
1La edad actual del padre es 35 y la del hijo es 5, mientras que  son los años que tienen que pasar para que se cumpla la condición dada
son los años que tienen que pasar para que se cumpla la condición dada
2Escribimos la condición dada en forma de ecuación
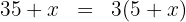
3Realizamos la multiplicación
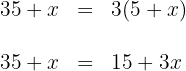
4Restamos  y
y  en ambos lados de la ecuación
en ambos lados de la ecuación

5Para despejar  , multiplicamos por
, multiplicamos por  ambos lados de la ecuación y simplificamos
ambos lados de la ecuación y simplificamos
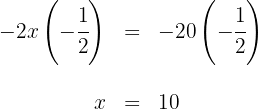
6Dentro de  años, la edad del padre será tres veces mayor que la de su hijo.
años, la edad del padre será tres veces mayor que la de su hijo.
Si al doble de un número se le resta su mitad resulta 54. ¿Cuál es el número?
1Como no conocemos el número solicitado, lo representamos por 
2Escribimos la condición dada en forma de ecuación
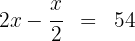
3Multiplicamos por 2 ambos lados de la ecuación
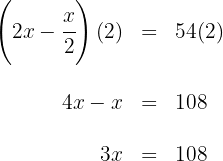
4Multiplicamos por  en ambos lados de la ecuación
en ambos lados de la ecuación
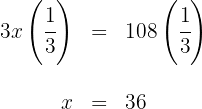
5El número buscado es 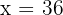
La base de un rectángulo es doble que su altura. ¿Cuáles son sus dimensiones si el perímetro mide 30 cm?
1Representamos la altura por  , por lo que su base es
, por lo que su base es 
2Escribimos la condición del perímetro en forma de ecuación

3Realizamos las multiplicaciones y sumamos términos semejantes

4Multiplicamos por  en ambos lados de la ecuación
en ambos lados de la ecuación
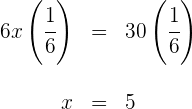
5La altura es 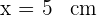 y su base es
y su base es 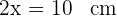
En una reunión hay doble número de mujeres que de hombres y triple número de niños que de hombres y mujeres juntos. ¿Cuántos hombres, mujeres y niños hay si la reunión la componen 96 personas?
1Representamos el número de hombres por  , por lo que el número de mujeres es
, por lo que el número de mujeres es  y el número de niños es
y el número de niños es 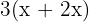
2Escribimos la condición dada en forma de ecuación
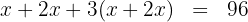
3Realizamos las multiplicaciones y sumamos términos semejantes
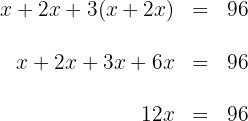
4Multiplicamos por 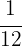 en ambos lados de la ecuación
en ambos lados de la ecuación
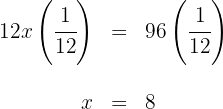
5El número de hombres es  , el de mujeres es
, el de mujeres es 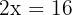 y el de niños es
y el de niños es 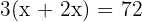
Se han consumido  de un bidón de aceite. Reponemos
de un bidón de aceite. Reponemos 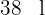 y el bidón ha quedado lleno hasta sus
y el bidón ha quedado lleno hasta sus  partes. Calcula la capacidad del bidón.
partes. Calcula la capacidad del bidón.
1Llamamos  a la capacidad del bidón y como hemos consumido
a la capacidad del bidón y como hemos consumido  de su capacidad quedará
de su capacidad quedará
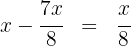
2Reponiendo 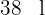 se escribe la segunda condición dada en forma de ecuación
se escribe la segunda condición dada en forma de ecuación

3Multiplicamos por el  en ambos lados de la ecuación
en ambos lados de la ecuación

4Restamos 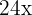 y
y  en ambos lados de la ecuación
en ambos lados de la ecuación
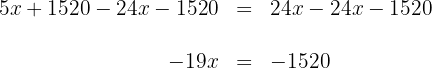
5Multiplicamos por 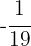 en ambos lados de la ecuación
en ambos lados de la ecuación

5La capacidad de bidón es 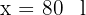
Una granja tiene cerdos y pavos, en total hay 35 cabezas y 116 patas. ¿Cuántos cerdos y pavos hay?
1Llamamos  a la cantidad de cabezas de cerdos y como en total hay 35 cabezas, entonces
a la cantidad de cabezas de cerdos y como en total hay 35 cabezas, entonces  es el número de cabezas de pavos
es el número de cabezas de pavos
2Escribimos la condición de las patas, para lo cual los cerdos cuentan con 4 patas y los pavos con 2

3Multiplicamos y luego sumamos términos semejantes

4Restamos  en ambos lados de la ecuación
en ambos lados de la ecuación
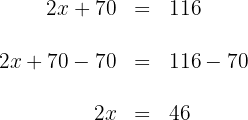
5Multiplicamos por  en ambos lados de la ecuación
en ambos lados de la ecuación

5Hay 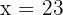 cerdos y
cerdos y 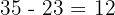 pavos.
pavos.
Luís hizo un viaje en el coche, en el cual consumió 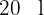 de gasolina. El trayecto lo hizo en dos etapas: en la primera, consumió
de gasolina. El trayecto lo hizo en dos etapas: en la primera, consumió  de la gasolina que tenía el depósito y en la segunda etapa, la mitad de la gasolina que le queda. Se pide la cantidad de litros de gasolina que se tenía en el depósito y los litros consumidos en cada etapa.
de la gasolina que tenía el depósito y en la segunda etapa, la mitad de la gasolina que le queda. Se pide la cantidad de litros de gasolina que se tenía en el depósito y los litros consumidos en cada etapa.
1Llamamos  a los litros de gasolina que tenía el depósito
a los litros de gasolina que tenía el depósito
2Escribimos la condición de la primera etapa

3Escribimos la condición de la segunda etapa

4Para encontrar la cantidad de gasolina que tenía el depósito, sumamos lo consumido en ambas etapas, lo cual es igual a 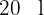
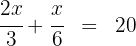
5Multiplicamos por  en ambos lados de la ecuación
en ambos lados de la ecuación
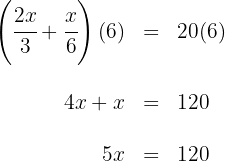
6Multiplicamos por  en ambos lados de la ecuación
en ambos lados de la ecuación
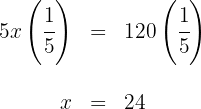
Así, el depósito tenía 
En la primera etapa se consumió  , mientras que en la segunda etapa se consumió
, mientras que en la segunda etapa se consumió 
En una librería, Ana compra un libro con la tercera parte de su dinero y un cómic con las dos terceras partes de lo que le quedaba. Al salir de la librería tenía 12 €. ¿Cuánto dinero tenía Ana?
1Llamamos  al total de dinero
al total de dinero
2Escribimos la condición del libro

3Escribimos la condición para el cómic
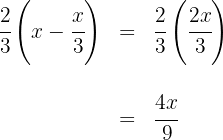
4Para encontrar la cantidad de dinero que tenía, sumamos los gastos del libro y el cómic junto con el dinero sobrante

5Multiplicamos por  en ambos lados de la ecuación y sumamos términos semejantes
en ambos lados de la ecuación y sumamos términos semejantes
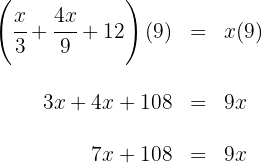
6Restamos 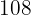 y
y 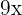 en ambos lados de la ecuación
en ambos lados de la ecuación
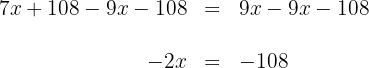
7Multiplicamos por  en ambos lados de la ecuación
en ambos lados de la ecuación
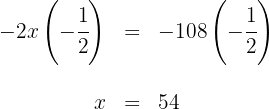
Así, Ana tenía  €
€
Un camión sale de una ciudad a una velocidad de 40 km/h. Una hora más tarde sale de la misma ciudad y en la misma dirección y sentido un coche a 60 km/h. Encuentra el tiempo que tardará en alcanzarle.
1Llamamos  al tiempo empleado por el camión, luego el tiempo empleado por el coche es
al tiempo empleado por el camión, luego el tiempo empleado por el coche es 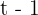
2Ambos vehículos recorren la misma distancia, por lo que
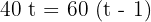
3Realizamos la multiplicación

4Restamos  en ambos lados de la ecuación
en ambos lados de la ecuación

5Multiplicamos por 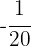 en ambos lados de la ecuación
en ambos lados de la ecuación
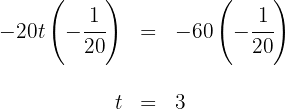
Así, para que los vehículos se alcancen, el camión emplea  mientras que el coche emplea
mientras que el coche emplea 
Las dos cifras de un número son consecutivas. La mayor es la de las decenas y la menor la de las unidades. El número es igual a seis veces la suma de las cifras. ¿Cuál es el número?
1Llamamos  a la cifra de la unidad, luego al ser consecutivas, la cifra de las decenas es
a la cifra de la unidad, luego al ser consecutivas, la cifra de las decenas es 
2Si tenemos un número de dos cifras, por ejemplo  podemos descomponerlo, de este modo:
podemos descomponerlo, de este modo:
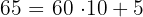
3Nuestro número de dos cifras es  , con la condición se obtiene
, con la condición se obtiene
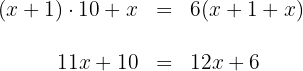
4Restamos 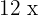 y
y  en ambos lados de la ecuación
en ambos lados de la ecuación

5Multiplicamos por  en ambos lados de la ecuación y se obtiene
en ambos lados de la ecuación y se obtiene 
Así, el número buscado es
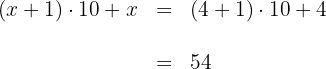
Supongamos que estás ahorrando dinero para comprar un nuevo teléfono celular que cuesta $700. Tienes un trabajo de medio tiempo y ganas $50 por día trabajado. Además, recibes una asignación semanal de $20 de tus padres. Supongamos que gastas $3 por cada día que vas a trabajar. Quieres saber cuántos días a la semana necesitas trabajar para poder comprar el teléfono celular en un cierto número de semanas. ¿Cuántos días a la semana necesitas trabajar para comprar el teléfono celular en 8 semanas?
Sea  el número de días que trabajamos por semana. Entonces, el monto neto por semana que generamos al trabajar es de
el número de días que trabajamos por semana. Entonces, el monto neto por semana que generamos al trabajar es de  . Ahora, vemos que gastamos
. Ahora, vemos que gastamos  semanales en transporte, y ganamos $20 semanales adicionales. Entonces, por semana generamos
semanales en transporte, y ganamos $20 semanales adicionales. Entonces, por semana generamos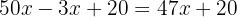
Entonces, en 8 semanas generamos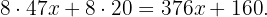
Si en este lapso necesitamos un mínimo de $700, obtenemos la siguiente ecuación: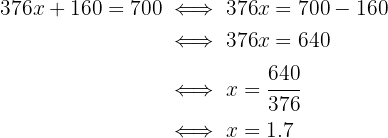
Es decir, si trabajamos al menos 1.7 días a la semana, podemos comprar el celular en 8 semanas.
Una tienda de ropa vende camisetas a un precio fijo de $15 cada una. Además, la tienda cobra un cargo de envío de $5 por cada pedido realizado. Un cliente quiere comprar un número desconocido de camisetas y está dispuesto a gastar un máximo de $80 en total, incluyendo el precio de las camisetas y el cargo de envío. ¿Cuántas camisetas puede comprar el cliente sin exceder su presupuesto de $80?
Sea 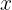 el número de camisetas que el cliente puede comprar. Entonces, la ecuación por considerar es
el número de camisetas que el cliente puede comprar. Entonces, la ecuación por considerar es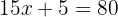
Entonces, despejamos para la variable: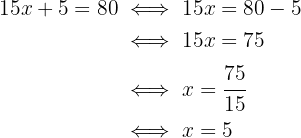
Es decir, el cliente con un presupuesto de $80 solo puede comprar a lo mas 5 camisetas.
Un estudiante trabaja durante el verano para ahorrar dinero para sus gastos escolares. Gana $8 por hora trabajada y planea trabajar un número de horas desconocido durante las vacaciones. Además, sus gastos escolares ascienden a $600. El estudiante quiere saber cuántas horas debe trabajar para cubrir sus gastos escolares. ¿Cuántas horas necesita trabajar? Si solo se le permite trabajar 6 horas diarias, ¿cuátos días debe trabajar?
Sea 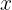 el número de horas que debe trabajar. Entonces, el dinero ganado se puede calcular de la siguiente manera:
el número de horas que debe trabajar. Entonces, el dinero ganado se puede calcular de la siguiente manera:
Dinero Ganado = (Dinero por hora) * (horas trabajadas)
Si necesitamos $600, entonces queremos que dinero ganado sea 600, y debemos depsejar para las horas trabajadas.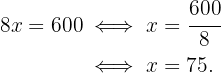
Es decir, debe trabajar 75 horas para completar su objetivo. Ahora bien, si solo puede trabajar 6 horas diarias, entonces debe trabajar por 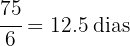
Como debe completar la jornada, debe trabajar por 13 dís completos.
Una empresa de envío ofrece dos tipos de tarifas para el envío de paquetes. La Tarifa A cobra un cargo fijo de $10 más $2 por cada libra de peso del paquete. La Tarifa B cobra un cargo fijo de $15 más $1.50 por cada libra de peso del paquete. ¿Cuánto debe pesar un paquete para que ambas tarifas cobren la misma cantidad?
Sea 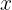 el peso del paquete que queremos enviar. Buscamos un peso tal que
el peso del paquete que queremos enviar. Buscamos un peso tal que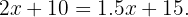
Entonces, depejamos para el peso: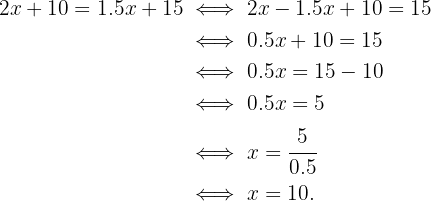
Entonces, para que ambas tarifas sean iguales, nuestro paquete debe pesar 10 libras.
Un cliente está comparando dos planes de telefonía celular. El Plan A ofrece un costo fijo mensual de $30 más $0.10 por minuto de llamadas. El Plan B ofrece un costo fijo mensual de $45 más $0.05 por minuto de llamadas. ¿Cuántos minutos debe utilizar el cliente para que ambos planes cobren la misma cantidad?
Sea 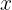 el número de minutos que el cliente utiliza. Entonces, buscamos una cantidad de minutos tal que
el número de minutos que el cliente utiliza. Entonces, buscamos una cantidad de minutos tal que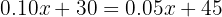
Es decir, un 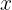 tal que la tarifa de ambos planes sean iguales.
tal que la tarifa de ambos planes sean iguales.
Entonces, depejamos para el tiempo en minutos: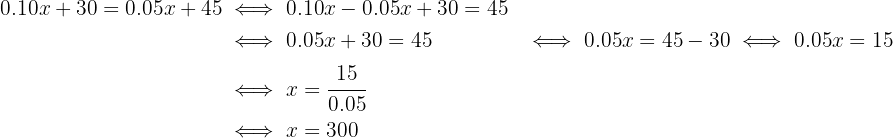
Entonces, a los 300 minutos de servicio, ambas tarifas coniciden.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Habéis cometido un error en el 2 de irracionales habéis puesto un 6 y es un 5
Una disculpa por que se brinca un paso pues el ejercicio es √x-1=5 y falto que √x=5+1, y aparece de repente √x=6.
Muy buenos ejercicios. Solamente una aclaración: en el problema 9 hay un error en la factorización del trinomio x2 – 28x + 169, los binomios serían: ( x – 21 )( x – 7 ) ; y no ( x – 21) ( x + 7 ). La ecuación tiene dos soluciones positivas, x = 21 y x = 21, pero la que da solución al problema es x = 21 por la condicionante «la edad que tenía hace 13 años»
Hola ya revise el ejercicio y la solución es (x-21)(x-7)=0, entonces los valores son x1=21, x=7, tal como lo indicas y no encontré el error que mencionas.
Factorización de un trinomio 2do grado
SRS. SUPERPROF.- CIENCIAS MATEMÁTICAS, REQUIERE DIFERENTES METODOLOGÍAS EN BIEN DE LOS EDUCANDOS. EL ESFUERZOS QUE VOSOTRO BRINDAN OBVIAMENTE ES EN BIEN DE NUESTRAS FUTURAS GENERACIONES. INFINITAS GRACIAS POR VUESTRAS HONORABLES DEDICACIONES. EN VERDAD, INFINITAS GRACIAS. DIOS LES ILUMINE POR SIEMPRE. BENDICIONES. AMEN.
Hola, con gusto te explicamos, podrías señalar cuales son las ecuaciones que no entiendes como se resolvieron y será un placer ayudarte.