Capítulos
Los sistemas de ecuaciones no lineales están formados por dos o más ecuaciones en las que al menos una no es lineal, es decir, contiene términos cuadráticos, cúbicos, raíces, productos de variables, funciones trigonométricas, exponenciales, entre otros. A diferencia de los sistemas lineales, resolver estos sistemas puede implicar métodos más avanzados y análisis más cuidadosos.
En esta sección se presentan ejercicios resueltos paso a paso que te permitirán practicar la resolución de sistemas no lineales mediante diferentes estrategias. El objetivo es ayudarte a identificar el enfoque adecuado según la estructura del sistema, interpretar los resultados y verificar si las soluciones encontradas satisfacen todas las ecuaciones dadas.

Ejercicios de sistemas de ecuaciones no lineales
Resuelve los siguientes sistemas de ecuaciones
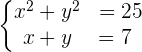
Resolveremos el sistema por sustitución. Primero, despejamos una incógnita de alguna de las ecuaciones, preferentemente de la de primer grado.

Después, sustituimos el valor de la incógnita despejada en la otra ecuación:
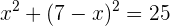
Ahora, resolvemos la ecuación resultante:

Luego, al dividir por 2, obtenemos la siguiente ecuación cuadrática,
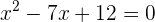
La solución de esta ecuación se obtiene mediante la fórmula general,

Por lo que las soluciones a la ecuación cuadrática son:

Cada uno de los valores obtenidos se sustituyen en la otra ecuación. De este modo, se obtienen los valores correspondientes de la otra incógnita.
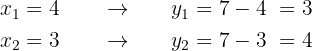
Por tanto, las soluciones al sistema son

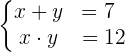
De nuevo, vamos a resolver el sistema por sustitución. Primero, despejamos la  de la primera ecuación:
de la primera ecuación:
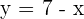
Después, sustituimos el valor de  en la segunda ecuación:
en la segunda ecuación:

Es decir,
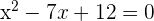
Ahora, resolvemos la ecuación resultante utilizando la fórmula general
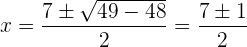
Así, las soluciones de la ecuación cuadrática son:

Por último, sustituimos en la otra ecuación cada uno de los valores que acabamos de obtener. Así, obtendremos los valores correspondientes de la otra incógnita:
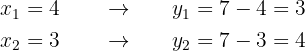
De esta manera, las soluciones al sistema no lineal son:

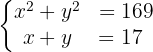
De nuevo, el sistema lo resolveremos utilizando sustitución. Primero, despejamos la  de la segunda ecuación:
de la segunda ecuación:

Sustituimos el valor de  en la primera ecuación
en la primera ecuación

Agrupamos términos semejantes y, después, dividimos por 2:
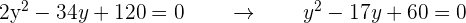
Resolvemos la ecuación resultante,
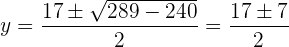
Por lo que la ecuación cuadrática tiene soluciones
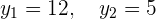
Sustituimos en la otra ecuación cada uno de los valores obtenidos. De esta manera, obtenemos los valores de la otra incógnita,
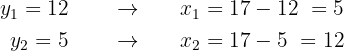
Por tanto, las soluciones son:
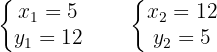
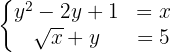
Resolvemos el sistema, de nuevo, por sustitución. Ya tenemos despejada la  en la primera ecuación, de manera que sustituimos el valor de
en la primera ecuación, de manera que sustituimos el valor de  en la segunda ecuación.
en la segunda ecuación.

Como es una ecuación radical elevamos al cuadrado en ambos lados de la ecuación (observa que primero dejamos la raíz sola del lado izquierdo de la ecuación):

Luego,
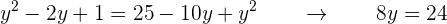
Por lo que  . Comprobamos la solución de la ecuación radical
. Comprobamos la solución de la ecuación radical

Es decir, 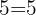 , por lo que
, por lo que  sí es solución de la ecuación radical. Sustituimos, en la otra ecuación, el valor obtenido. Así, obtenemos el valor de la otra incógnita:
sí es solución de la ecuación radical. Sustituimos, en la otra ecuación, el valor obtenido. Así, obtenemos el valor de la otra incógnita:
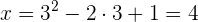
Así, nuestra solución es:
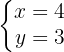
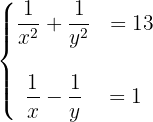
Para resolver el sistema en primer lugar vamos a realizar dos cambios de variable:
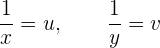
Sustituimos los cambios de variable en el sistema,
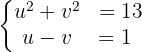
Ya tenemos un sistema que es más fácil de resolver. De nuevo resolveremos este sistema por sustitución. Despejamos  de la segunda ecuación, lo que nos da
de la segunda ecuación, lo que nos da  . Si sustituimos en la primera ecuación, tenemos
. Si sustituimos en la primera ecuación, tenemos
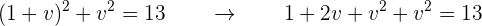
Que, al igualar a cero y dividir por 2, obtenemos,

Resolvemos la ecuación resultante por medio de la fórmula general,
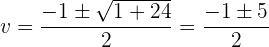
Por lo que tenemos
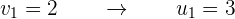
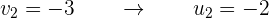
Deshacemos el cambio y cada uno de los valores obtenidos se sustituyen en la otra ecuación, se obtienen así los valores correspondientes de la otra incógnita
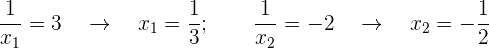
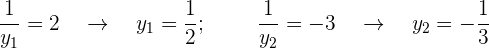
Así, las soluciones son:

Problemas que utilizan sistemas de ecuaciones no lineales
El producto de dos números es 4, y la suma de sus cuadrados 17. ¿Cuáles son esos números?
Para resolver este problema, primero debemos expresarlo de manera algebraica. Observemos primero que "el producto de dos números es 4" se puede expresar algebraicamente como 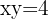 . Similarmente, "la suma de sus cuadrados (de estos dos números) es 17" se expresa algebraicamente como
. Similarmente, "la suma de sus cuadrados (de estos dos números) es 17" se expresa algebraicamente como 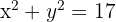 . Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
. Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
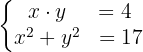
Resolveremos por sustitución. Primero, despejamos  de la primera ecuación,
de la primera ecuación,
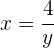
Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
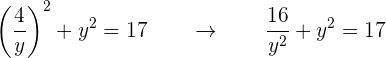
Es decir,
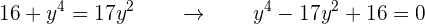
Por lo que obtenemos una ecuación bicuadrada, la cual debemos resolver. Para resolverla, utilizamos el cambio de variable 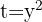 . Al sustituir este cambio de variable obtenemos,
. Al sustituir este cambio de variable obtenemos,

El cual resolvemos utilizando la fórmula general,
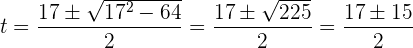
De modo que las soluciones de la ecuación bicuadrada son
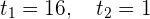
Esto implica que

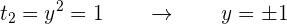
Es decir, tenemos 4 posibles valores para  . Por lo tanto, al sustituir estos valores en la primera ecuación, tenemos,
. Por lo tanto, al sustituir estos valores en la primera ecuación, tenemos,
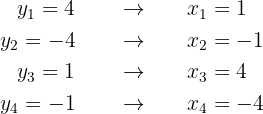
Así, las 4 soluciones del problema son:
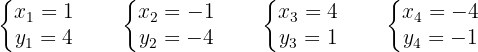
Hallar dos números positivos tales que la suma de sus cuadrados es 100 y la diferencia de los cuadrados es 28
Para resolver este problema, primero debemos expresarlo de manera algebraica. Observemos primero que "la suma de sus cuadrados es 100" se puede expresar algebraicamente como 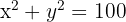 . Similarmente, "la diferencia de sus cuadrados es 28" se expresa algebraicamente como
. Similarmente, "la diferencia de sus cuadrados es 28" se expresa algebraicamente como 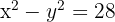 . Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
. Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
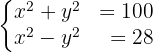
Resolveremos por reducción y obtenemos
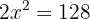
Despejamos 
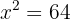
Es decir,
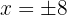
Sustituimos en la primera ecuación
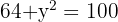
Resolviendo obtenemos
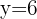 ; así los números buscados son 8 y 6.
; así los números buscados son 8 y 6.¿Cuáles son los lados de dos cuadrados si la suma de sus áreas es 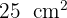 y su diferencia es de
y su diferencia es de 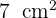 ?
?
Para resolver este problema, primero debemos expresarlo de manera algebraica. Observemos primero que "la suma de sus áreas es 25" se puede expresar algebraicamente como 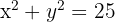 . Similarmente, "la diferencia de sus áreas es 7" se expresa algebraicamente como
. Similarmente, "la diferencia de sus áreas es 7" se expresa algebraicamente como 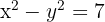 . Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
. Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
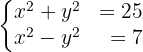
Resolveremos por reducción y obtenemos
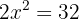
Despejamos 
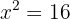
Es decir,
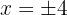
Sustituimos en la primera ecuación
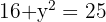
Resolviendo obtenemos
 ; así los lados buscados son 3 y 4.
; así los lados buscados son 3 y 4.Un triángulo tiene un área de 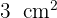 y la suma del cuadrado de su altura y el cuadrado de su base es
y la suma del cuadrado de su altura y el cuadrado de su base es 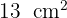 . Si la base es menor que la altura, encuentra las dimensiones del triángulo.
. Si la base es menor que la altura, encuentra las dimensiones del triángulo.
Para resolver este problema, primero debemos expresarlo de manera algebraica. Observemos primero que "el área es 6" se puede expresar algebraicamente como 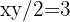 . Similarmente, "la suma de los cuadrados de la base y la altura es 13" se expresa algebraicamente como
. Similarmente, "la suma de los cuadrados de la base y la altura es 13" se expresa algebraicamente como 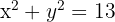 . Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
. Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:
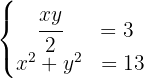
Resolveremos por sustitución
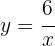
Sustituimos el valor  en la segunda ecuación
en la segunda ecuación
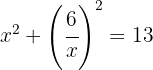
Resolviendo, obtenemos la ecuación
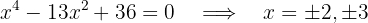
Sustituimos en la primera ecuación
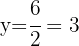
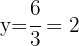
Así, las medidas buscadas son: son base igual a 2 cm y altura igual a 3 cm.
Halla una fracción equivalente a 5/7 cuyos términos elevados al cuadrado sumen 1184
Para expresar algebraicamente este problema, la fracción equivalente tendrá como numerador  y como denominador
y como denominador  . De este modo, el problema se resuelve utilizando el siguiente sistema no lineal:
. De este modo, el problema se resuelve utilizando el siguiente sistema no lineal:
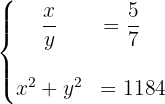
Resolvemos el sistema por sustitución. Despejamos primero la  de la primera ecuación:
de la primera ecuación:

Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
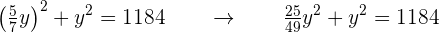
Así

Es decir,
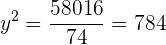
Resolvemos esta ecuación de segundo grado,
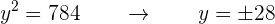
Luego, sustituimos en la otra ecuación cada uno de los valores obtenidos:

Por lo tanto, las fracciones equivalentes a 5/7 son
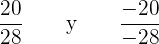
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Habéis cometido un error en el 2 de irracionales habéis puesto un 6 y es un 5
Una disculpa por que se brinca un paso pues el ejercicio es √x-1=5 y falto que √x=5+1, y aparece de repente √x=6.
Muy buenos ejercicios. Solamente una aclaración: en el problema 9 hay un error en la factorización del trinomio x2 – 28x + 169, los binomios serían: ( x – 21 )( x – 7 ) ; y no ( x – 21) ( x + 7 ). La ecuación tiene dos soluciones positivas, x = 21 y x = 21, pero la que da solución al problema es x = 21 por la condicionante «la edad que tenía hace 13 años»
Hola ya revise el ejercicio y la solución es (x-21)(x-7)=0, entonces los valores son x1=21, x=7, tal como lo indicas y no encontré el error que mencionas.
Factorización de un trinomio 2do grado
SRS. SUPERPROF.- CIENCIAS MATEMÁTICAS, REQUIERE DIFERENTES METODOLOGÍAS EN BIEN DE LOS EDUCANDOS. EL ESFUERZOS QUE VOSOTRO BRINDAN OBVIAMENTE ES EN BIEN DE NUESTRAS FUTURAS GENERACIONES. INFINITAS GRACIAS POR VUESTRAS HONORABLES DEDICACIONES. EN VERDAD, INFINITAS GRACIAS. DIOS LES ILUMINE POR SIEMPRE. BENDICIONES. AMEN.
Hola, con gusto te explicamos, podrías señalar cuales son las ecuaciones que no entiendes como se resolvieron y será un placer ayudarte.