y
son opuestos en el plano, si la suma de sus medidas es igual a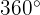
o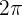
radianes, esto es,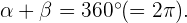
De esta forma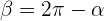 
. Adicionalmente tenemos las siguientes relaciones para la resta de ángulos de las funciones seno, coseno y tangente,
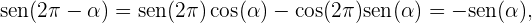
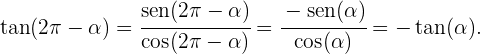
Ejemplo
1 Dado el ángulos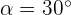
, calcular su ángulo opuesto y además sus respectivos valores para las funciones seno, coseno y tangente. Primero consideramos la siguiente figura 
De la figura podemos notar que el ángulo opuesta es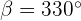
, en efecto
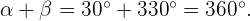
Ahora para las funciones seno, coseno y tangente tenemos lo siguiente
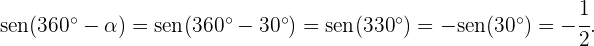
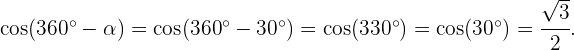
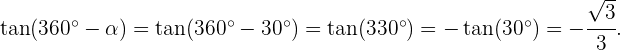
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cálculo el lado bc aplicando la ley de cosenos b=5cm c=6cm a=60°
Materia:
erica V= 1
Calcula el lado BC aplicando
5
V
0
V
4
V
A
B
AB = 6cm
CR
Datos
0 =5cm
C=600
En un triángulo, se tienen los datos: A = 50° ,B = 65° y a = 12. Encuentra el lado b.
Me pueden ayudar en este ejercicio
3 tan 150⁰+2 cos 210⁰/ Cos 2π. Sen 315
excelente, por ejemplo tengo uno donde me hacen falta el ángulo A, B, C tengo estos datos lado a:14, b:6, c:4
La respuesta es 14.197
¿ porqué no hay un modo de resolver triángulos sin la necesidad de aplicar la Trigonometria académica ? Saludos, profesor.
Hola, posiblemente exista otro método, pero por desgracia es todavía mas difícil que la trigonometría académica incluso te puedo asegurar que hoy en día es mas fácil y mas directo resolver los problemas de triángulos, entendemos que a veces llega a ser confuso pero te aseguramos que este método es el mas sencillo que existe.
Resuelve esto bien y claro.
¿Cuánto le falta al complemento del suplemento de 165,315° para alcanzar el suplemento del complemento de π/12 rad?