Capítulos

Identidades trigonométricas fundamentales
1 Relación entre seno y coseno
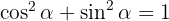
2 Relación entre secante y tangente
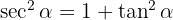
3 Relación entre cosecante y cotangente

4 Funciones trigonométricas recíprocas
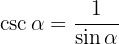
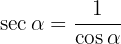

Ejemplos de ejercicios con identidades trigonométricas fundamentales
Sabiendo que 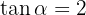 , y que
, y que  , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 
Obtengamos las demás funciones trigonométricas evaluadas en dicho ángulo. Empezaremos con  ya que la podemos obtener directamente de
ya que la podemos obtener directamente de 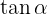
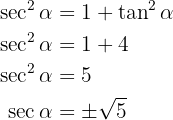
Sin embargo, notemos que para el cuadrante (o rango) donde está definido  , se cumple que
, se cumple que 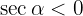 , por lo tanto, tenemos que
, por lo tanto, tenemos que 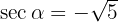 .
.
Ahora podemos obtener el 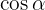
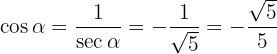
Obtengamos el 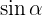 y de este el
y de este el 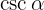 . Al igual que con el
. Al igual que con el 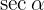 , se tiene que seno es negativo para el cuadrante en el cual está definido
, se tiene que seno es negativo para el cuadrante en el cual está definido  , así
, así
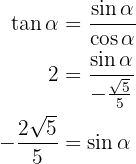
Así ya obtuvimos 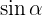 , ahora notemos que
, ahora notemos que
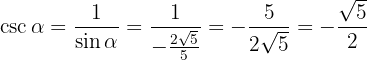
Por último, obtengamos 
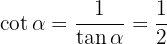
Sabiendo que se cumple que 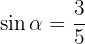 , y que
, y que 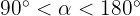 , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 
Obtengamos las demás funciones trigonométricas evaluadas en dicho ángulo. Empezaremos con 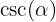 ya que la podemos obtener directamente
ya que la podemos obtener directamente

Ahora podemos obtener el 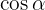 , notemos que por el intervalo donde está definido
, notemos que por el intervalo donde está definido  se cumple que el coseno es negativo, así
se cumple que el coseno es negativo, así
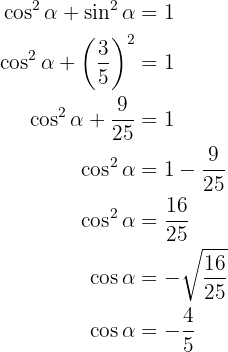
Ya que tenemos el coseno, podemos obtener 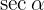 directamente
directamente

Ya solo nos falta obtener tangente y cotangente, estas las obtenemos de a partir del seno y el coseno

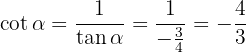
Razones trigonométricas de la suma y diferencia de ángulos
1. 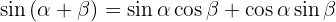
2. 
3. 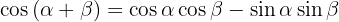
4. 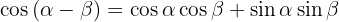
5. 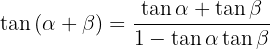
6. 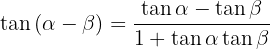
Ejemplos de ejercicios con suma y diferencia de ángulos
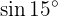
Para resolver este ejercicio escribiremos nuestro ángulo como la suma de dos ángulos específicos, esto con el fin de utilizar las fórmulas de las funciones trigonométricas aplicada en suma y resta de ángulos
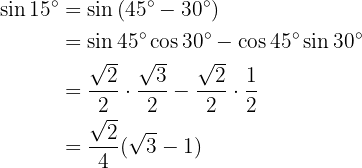

Para resolver este ejercicio escribiremos nuestro ángulo como la suma de dos ángulos específicos, esto con el fin de utilizar las fórmulas de las funciones trigonométricas aplicada en suma y resta de ángulos
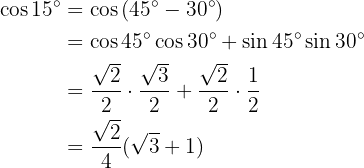
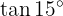
Para resolver este ejercicio escribiremos nuestro ángulo como la suma de dos ángulos específicos, esto con el fin de utilizar las fórmulas de las funciones trigonométricas aplicada en suma y resta de ángulos
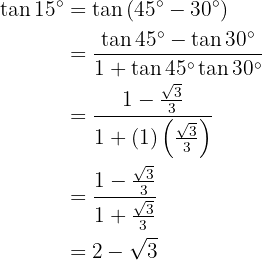
Razones trigonométricas del ángulo doble
1. 
2. 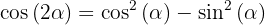
3. 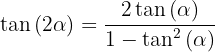
Ejemplos de ejercicios con ángulo doble
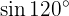
Para resolver este ejercicio primero encontraremos la mitad del ángulo dado y posteriormente utilizaremos la fórmula de la función trigonométrica de ángulo doble correspondiente:
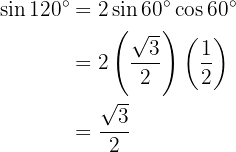
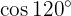
Para resolver este ejercicio primero encontraremos la mitad del ángulo dado y posteriormente utilizaremos la fórmula de la función trigonométrica de ángulo doble correspondiente:
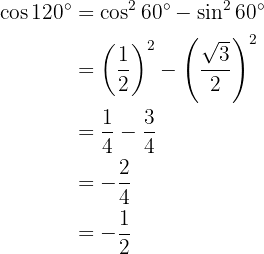
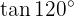
Para resolver este ejercicio primero encontraremos la mitad del ángulo dado y posteriormente utilizaremos la fórmula de la función trigonométrica de ángulo doble correspondiente:
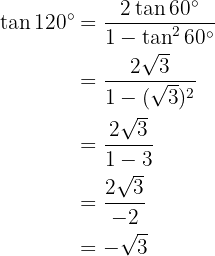
Razones trigonométricas del ángulo mitad
1. 
2. 
3. 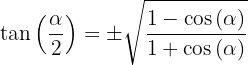
Ejemplos de ejercicios del ángulo mitad
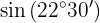
Para resolver este ejercicio primero obtendremos el doble del ángulo dado y posteriormente aplicaremos la fórmula correspondiente a la función trigonométrica dada. Notemos que por el cuadrante donde está el ángulo, el valor del seno será positivo.
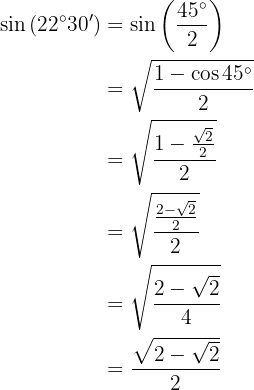

Para resolver este ejercicio primero obtendremos el doble del ángulo dado y posteriormente aplicaremos la fórmula correspondiente a la función trigonométrica dada. Notemos que por el cuadrante donde está el ángulo, el valor del coseno será positivo.
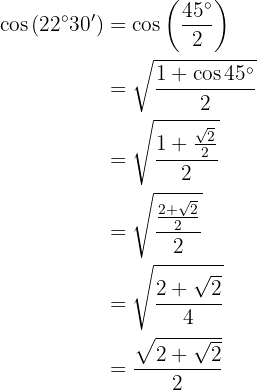
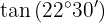
Para resolver este ejercicio primero obtendremos el doble del ángulo dado y posteriormente aplicaremos la fórmula correspondiente a la función trigonométrica dada. Notemos que por el cuadrante donde está el ángulo, el valor de la tangente será positivo.
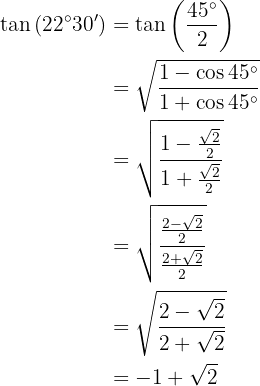
Transformación de operaciones
Transformaciones de sumas en productos
1. 
2. 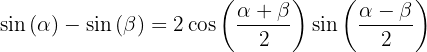
3. 
4. 
Ejemplos de transformaciones de sumas en productos
En los próximos ejercicio no escribiremos el valor de la suma, o diferencia, de la suma de las funciones trigonométricas, simplemente la transformaremos a producto de otras funciones trigonométricas, según sea la fórmula que se deba aplicar.
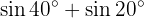
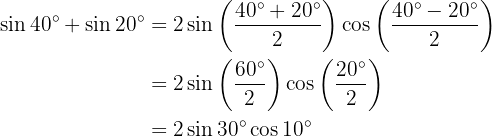
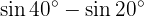
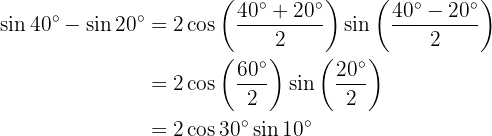
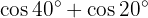
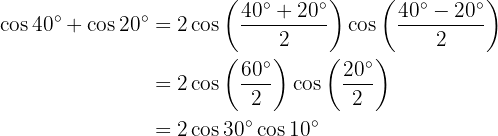
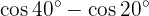
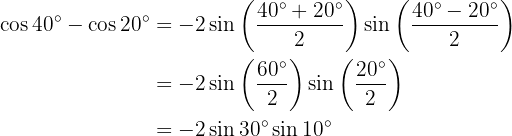
Transformaciones de productos en sumas
1. 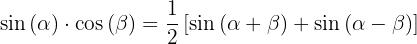
2. 
3. 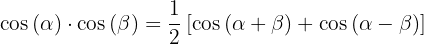
4. 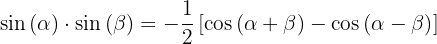
Ejemplos de transformaciones de productos en sumas
En los próximos ejercicio no escribiremos el valor de la multiplicación de las funciones trigonométricas, simplemente la transformaremos a la suma, o diferencia, de otras funciones trigonométricas, según sea la fórmula que se deba aplicar.
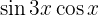

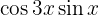
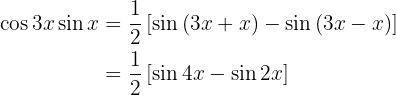
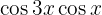
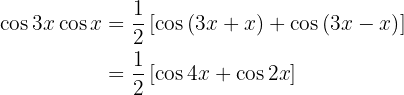

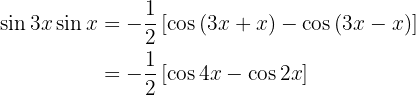
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cálculo el lado bc aplicando la ley de cosenos b=5cm c=6cm a=60°
Materia:
erica V= 1
Calcula el lado BC aplicando
5
V
0
V
4
V
A
B
AB = 6cm
CR
Datos
0 =5cm
C=600
En un triángulo, se tienen los datos: A = 50° ,B = 65° y a = 12. Encuentra el lado b.
excelente, por ejemplo tengo uno donde me hacen falta el ángulo A, B, C tengo estos datos lado a:14, b:6, c:4
La respuesta es 14.197
¿ porqué no hay un modo de resolver triángulos sin la necesidad de aplicar la Trigonometria académica ? Saludos, profesor.
Hola, posiblemente exista otro método, pero por desgracia es todavía mas difícil que la trigonometría académica incluso te puedo asegurar que hoy en día es mas fácil y mas directo resolver los problemas de triángulos, entendemos que a veces llega a ser confuso pero te aseguramos que este método es el mas sencillo que existe.
Resuelve esto bien y claro.
¿Cuánto le falta al complemento del suplemento de 165,315° para alcanzar el suplemento del complemento de π/12 rad?
como resolver este ejercicio (tag x )2 -1
_________= -(tag x )2
(cotag x )2 -1