¡Bienvenido a nuestra página dedicada a ejercicios de resolución de triángulos! ¿Alguna vez te has preguntado cómo determinar la longitud de un lado desconocido de un triángulo? ¿O cómo encontrar esos ángulos ocultos que desafían tu intuición? Nuestro objetivo es brindarte las herramientas y técnicas necesarias para resolver estos acertijos geométricos con facilidad.
Acompáñanos a explorar los diferentes métodos para resolver triángulos, desde el clásico Teorema de Pitágoras hasta las sofisticadas Leyes de Senos y Cosenos. Tambén, aprenderemos sobre triángulos especiales y sus propiedades únicas, y cómo aplicar esta información en situaciones del mundo real.
Estamos seguros de que esta serie de ejercicios que hemos diseñado para ti te servirán para que te conviertas en todo un experto en la resolución de tríangulos. !Adelante!
De un triángulo rectángulo  , se conocen
, se conocen  y
y 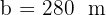 . Resolver el triángulo.
. Resolver el triángulo.

1Expresamos el seno del ángulo 
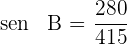
Aplicamos la función 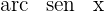 a ambos lados de la ecuación y se obtiene
a ambos lados de la ecuación y se obtiene

2El ángulo 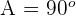 . Calculamos el ángulo
. Calculamos el ángulo 
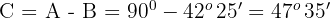
3Para calcular el lado  empleamos la función coseno para el ángulo
empleamos la función coseno para el ángulo 
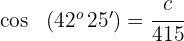
Despejamos  y resolvemos
y resolvemos
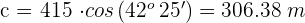
De un triángulo rectángulo  , se conocen
, se conocen  y
y 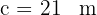 . Resolver el triángulo.
. Resolver el triángulo.

1Expresamos la tangente del ángulo 

Aplicamos la función  a ambos lados de la ecuación y se obtiene
a ambos lados de la ecuación y se obtiene

2El ángulo 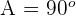 . Calculamos el ángulo
. Calculamos el ángulo 
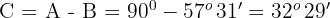
3Para calcular el lado  empleamos la función seno para el ángulo
empleamos la función seno para el ángulo 
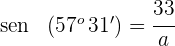
Despejamos  y resolvemos
y resolvemos
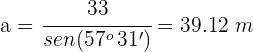
De un triángulo rectángulo  , se conocen
, se conocen 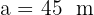 y
y  . Resolver el triángulo.
. Resolver el triángulo.

1El ángulo 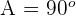 . Calculamos el ángulo
. Calculamos el ángulo 
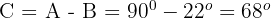
2Expresamos el seno del ángulo 
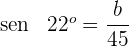
Despejamos  y resolvemos
y resolvemos
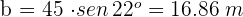
3Para calcular el lado  empleamos la función coseno para el ángulo
empleamos la función coseno para el ángulo 
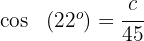
Despejamos  y resolvemos
y resolvemos
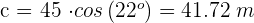
De un triángulo rectángulo  , se conocen
, se conocen  y
y 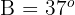 . Resolver el triángulo
. Resolver el triángulo

1El ángulo 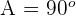 . Calculamos el ángulo
. Calculamos el ángulo 
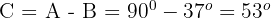
2Expresamos el seno del ángulo 

Despejamos  y resolvemos
y resolvemos
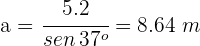
3Para calcular el lado  empleamos la función tangente para el ángulo
empleamos la función tangente para el ángulo 
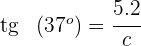
Despejamos  y resolvemos
y resolvemos

Un dirigible que está volando a  de altura, distingue un pueblo con un ángulo de depresión de
de altura, distingue un pueblo con un ángulo de depresión de  . ¿A qué distancia del pueblo se halla?
. ¿A qué distancia del pueblo se halla?
1Representamos gráficamente los datos proporcionados

2Expresamos la tangente del ángulo 

Despejamos la distancia  y resolvemos
y resolvemos
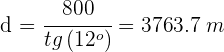
Hallar el radio de una circunferencia sabiendo que una cuerda de 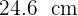 tiene como arco correspondiente uno de
tiene como arco correspondiente uno de 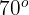 .
.
1Representamos gráficamente los datos proporcionados

2Se forma un triángulo isósceles cuyos lados iguales corresponden al radio de la circunferencia. Consideramos 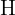 el punto medio del segmento
el punto medio del segmento  , luego el triángulo
, luego el triángulo 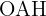 es rectángulo y
es rectángulo y 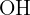 bisecta al ángulo
bisecta al ángulo 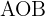
3Calculamos el seno del ángulo 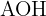
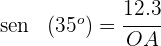
Despejamos la distancia  y resolvemos
y resolvemos
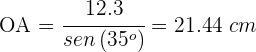
Así, el radio buscado es 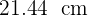 .
.
Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 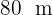 y
y 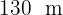 , y forman entre ellos un ángulo de
, y forman entre ellos un ángulo de 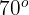 .
.
1Representamos gráficamente los datos proporcionados

2Calculamos la altura  del triángulo, para ello calculamos el seno de
del triángulo, para ello calculamos el seno de 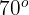
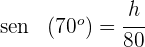
3Despejamos  y resolvemos
y resolvemos

El área solicitada es
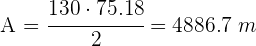
Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 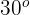 y si nos acercamos
y si nos acercamos  , bajo un ángulo de
, bajo un ángulo de 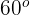 .
.
1Representamos gráficamente los datos proporcionados

2Calculamos la tangente de 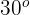 y despejamos
y despejamos 

3Calculamos la tangente de 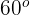 y despejamos
y despejamos 
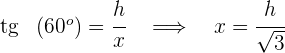
Igualamos ambos valores de  y resolvemos para
y resolvemos para 
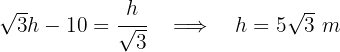
La longitud del lado de un octógono regular es  . Hallar los radios de la circunferencia inscrita y circunscrita.
. Hallar los radios de la circunferencia inscrita y circunscrita.
1Representamos gráficamente los datos proporcionados

2El ángulo 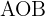 es igual a
es igual a 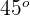 , por lo que el ángulo
, por lo que el ángulo  es igual a
es igual a  . Para calcular el radio de la circunferencia inscrita empleamos
. Para calcular el radio de la circunferencia inscrita empleamos
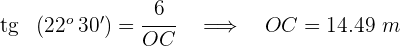
3Para calcular el radio de la circunferencia circunscrita empleamos

Calcular la longitud del lado y de la apotema de un octógono regular inscrito en una circunferencia de 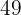 centímetros de radio.
centímetros de radio.
1Representamos gráficamente los datos proporcionados

2El ángulo 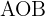 es igual a
es igual a 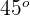 , por lo que si trazamos la bisectriz, al tratarse de un triángulo isósceles, se obtienen dos triángulos rectángulos iguales. Para calcular el lado empleamos
, por lo que si trazamos la bisectriz, al tratarse de un triángulo isósceles, se obtienen dos triángulos rectángulos iguales. Para calcular el lado empleamos

3Para calcular el apotema empleamos
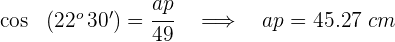
Tres pueblos A, B y C están unidos por carreteras. La distancia de A a C es  km y la de B a C es
km y la de B a C es  km. El ángulo que forman estas carreteras es
km. El ángulo que forman estas carreteras es  . ¿Cuánto distan A y B?
. ¿Cuánto distan A y B?
1Representamos gráficamente los datos proporcionados y construimos un triángulo rectángulo  de modo que
de modo que  se encuentre en el segmento
se encuentre en el segmento 

2Calculamos la altura
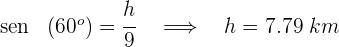
3Calculamos la distancia 
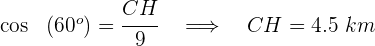
4Calculamos la distancia  empleando el teorema de Pitágoras
empleando el teorema de Pitágoras
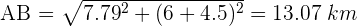
De un triángulo  , se conocen
, se conocen 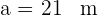 ,
,  y
y 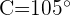 . Resolver el triángulo.
. Resolver el triángulo.

Para resolver el triágulo debemos encontrar los valores de el ángulo  y de los lados
y de los lados  y
y  .
.
Para encontrar el ángulo restante utilizamos que

Así,

Para encontrar los lados restantes del triángulo, utilizamos el Teorema del seno:

Por lo tanto,

Similarmente,

De un triángulo  , se conocen
, se conocen 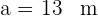 ,
,  y
y  . Resolver el triángulo.
. Resolver el triángulo.
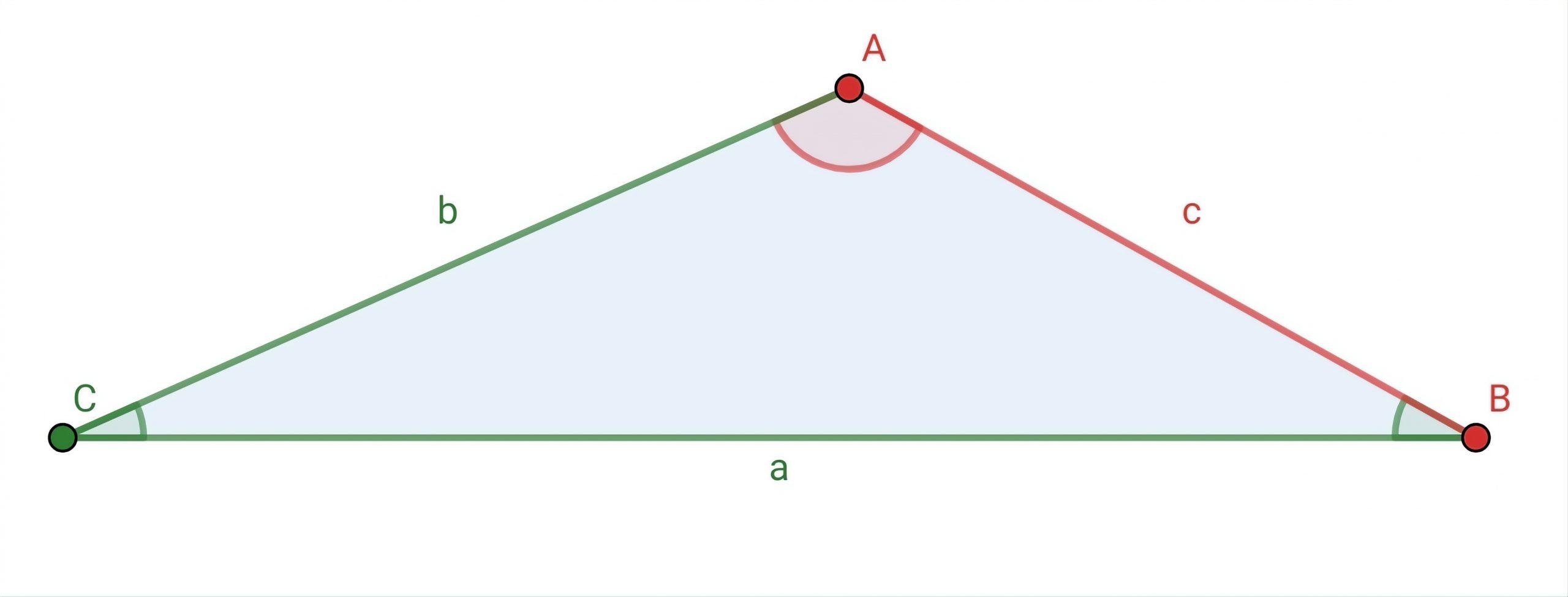
Para resolver el triágulo debemos encontrar el valor del lado  y de los ángulos
y de los ángulos  y
y  .
.
Para encontrar el ángulo restante utilizamos el Teorema del coseno:
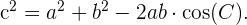
Así,
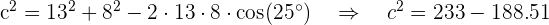
Entonces
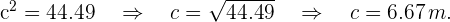
Para encontrar los ángulos, nuevamente utilizamos el Teorema del coseno:
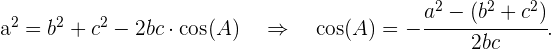
Así,
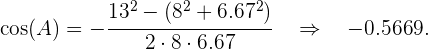
Por lo tanto,

Finalmente, si
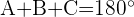
entonces
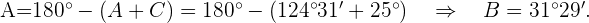
De un triángulo rectángulo  , se conocen
, se conocen 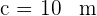 y
y 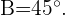 Calcula su área.
Calcula su área.

Para calcular el área primero encontraremos la base y la altura del triángulo, en este caso corresponden a los lados  y
y  .
.
Tenemos que 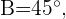 así
así

Por otro lado, también sabemos que
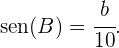
Dado esto, se tiene que
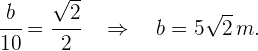
Del Teorema de Pitágoras se sigue que
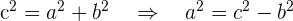
Esto implica que
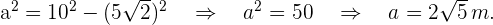
Finalmente, el área del triángulo es
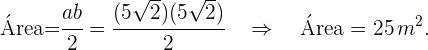
De un triángulo  , se conocen
, se conocen  ,
, 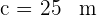 y
y  . Calcula su área.
. Calcula su área.

Para calcular el área de dicho triángulo utilizamos la fórmula

Por lo tanto,
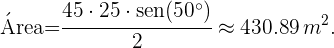
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cálculo el lado bc aplicando la ley de cosenos b=5cm c=6cm a=60°
Materia:
erica V= 1
Calcula el lado BC aplicando
5
V
0
V
4
V
A
B
AB = 6cm
CR
Datos
0 =5cm
C=600
En un triángulo, se tienen los datos: A = 50° ,B = 65° y a = 12. Encuentra el lado b.
excelente, por ejemplo tengo uno donde me hacen falta el ángulo A, B, C tengo estos datos lado a:14, b:6, c:4
La respuesta es 14.197
¿ porqué no hay un modo de resolver triángulos sin la necesidad de aplicar la Trigonometria académica ? Saludos, profesor.
Hola, posiblemente exista otro método, pero por desgracia es todavía mas difícil que la trigonometría académica incluso te puedo asegurar que hoy en día es mas fácil y mas directo resolver los problemas de triángulos, entendemos que a veces llega a ser confuso pero te aseguramos que este método es el mas sencillo que existe.
Resuelve esto bien y claro.
¿Cuánto le falta al complemento del suplemento de 165,315° para alcanzar el suplemento del complemento de π/12 rad?
como resolver este ejercicio (tag x )2 -1
_________= -(tag x )2
(cotag x )2 -1