A lo largo de este artículo, encontrarás una serie de problemas resueltos que te permitirán comprender mejor el comportamiento y las aplicaciones de los triángulos rectángulos. Los problemas abordarán temas como el uso de las relaciones entre las razones trigonométricas (seno, coseno y tangente) y el cálculo de longitudes y ángulos desconocidos. Con cada ejercicio resuelto, afianzarás conceptos clave para que desarrolles habilidades prácticas para enfrentar una variedad de situaciones geométricas.
Resuelve los siguientes ejercicios:
De un triángulo rectángulo  , se tiene la siguiente información: la hipotenusa es
, se tiene la siguiente información: la hipotenusa es  y uno de los catetos es
y uno de los catetos es 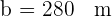 . Resolver el triángulo.
. Resolver el triángulo.
Resolver el triángulo significa encontrar cuánto mide el lado faltante y el valor de todos los ángulo en este. Notemos que al ser un triángulo rectángulo, sabemos que el ángulo  .
.

Aplicando seno tenemos que
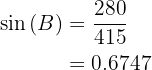
Aplicando arcoseno tenemos que el ángulo vale . Ahora, una vez que tenemos dos ángulo, podemos calcular de manera inmediata el último;
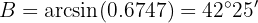
Ahora, una vez que tenemos dos ángulo, podemos calcular de manera inmediata el último:

Aplicando coseno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
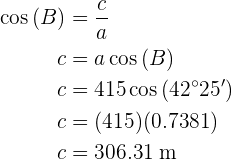
Así ya obtuvimos los datos faltantes.
De un triángulo rectángulo  , se conocen los catetos
, se conocen los catetos 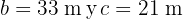 . Resolver el triángulo.
. Resolver el triángulo.
Resolver el triángulo significa encontrar los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo, también tenemos que el ángulo 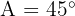 .
.
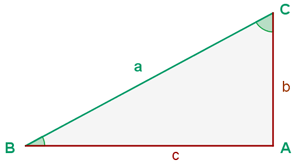
Para encontrar el ángulo  calcularemos su tangente y luego aplicaremos arcotangente:
calcularemos su tangente y luego aplicaremos arcotangente:
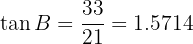
Entonces, tenemos que aplicando arcotangente 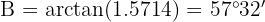 . Ahora, con esto tenemos dos ángulos, así, podemos calcular directamente el tercero,
. Ahora, con esto tenemos dos ángulos, así, podemos calcular directamente el tercero,  :
:
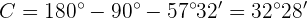
Por último, para obtener el valor del lado  utilizaremos la fórmula del seno y la aplicaremos al ángulo
utilizaremos la fórmula del seno y la aplicaremos al ángulo  , luego despejaremos
, luego despejaremos  para encontrar su valor.
para encontrar su valor.
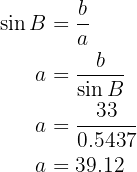
Así, hemos obtenido los datos faltantes.
De un triángulo rectángulo  , se conoce la hipotenusa y uno de los ángulos, cuyos valores son
, se conoce la hipotenusa y uno de los ángulos, cuyos valores son 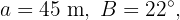 , respectivamente. Resolver el triángulo.
, respectivamente. Resolver el triángulo.
Resolver un triángulo significa encontrar los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo implica que  .
.

Al conocer dos de los tres ángulos podemos obtener de forma directa el tercero,  :
:
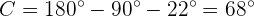
Para obtener el lado  aplicaremos seno sobre el ángulo
aplicaremos seno sobre el ángulo  y despejaremos
y despejaremos  :
:
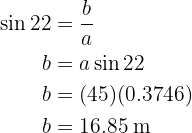
Para obtener el lado  aplicaremos coseno sobre el ángulo
aplicaremos coseno sobre el ángulo  y despejaremos
y despejaremos  :
:
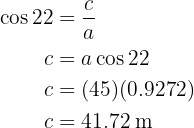
Así, hemos encontrado los lados y ángulos faltantes.
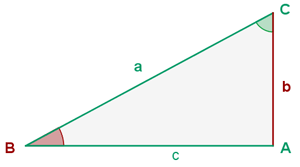
De un triángulo rectángulo  , se conoce un cateto y un ángulo
, se conoce un cateto y un ángulo 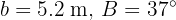 . Resolver el triángulo.
. Resolver el triángulo.
Obtengamos los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo, ya conocemos de antemano el ángulo  .
.
Dado que conocemos ya dos de los tres ángulos, podemos calcular el faltante,  , de manera directa
, de manera directa
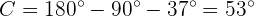
Para obtener el lado  aplicaremos seno sobre el ángulo
aplicaremos seno sobre el ángulo  y despejaremos
y despejaremos  :
:
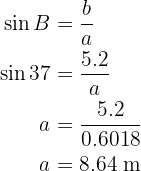
Para obtener el lado  aplicaremos cotangente sobre el ángulo
aplicaremos cotangente sobre el ángulo  y despejaremos
y despejaremos  :
:
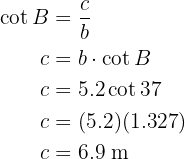
Hemos encontrados los lados y ángulos faltantes.
De un triángulo rectángulo  , se conoce la hipotenusa y un ángulo
, se conoce la hipotenusa y un ángulo 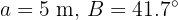 . Resolver el triángulo.
. Resolver el triángulo.
Obtengamos los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo, ya conocemos de antemano el ángulo  .
.

Dado que conocemos ya dos de los tres ángulos, podemos calcular el faltante,  , de manera directa
, de manera directa
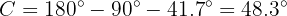
Para obtener el lado  aplicaremos seno sobre el ángulo
aplicaremos seno sobre el ángulo  y despejaremos
y despejaremos  :
:
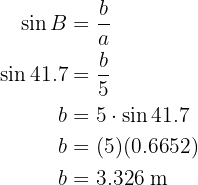
Para obtener el lado  aplicaremos coseno sobre el ángulo
aplicaremos coseno sobre el ángulo  y despejaremos
y despejaremos  :
:
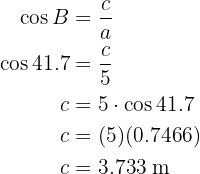
Hemos encontrados los lados y ángulos faltantes.
De un triángulo rectángulo  , se conoce un cateto y un ángulo
, se conoce un cateto y un ángulo 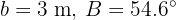 . Resolver el triángulo.
. Resolver el triángulo.
Obtengamos los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo, ya conocemos de antemano el ángulo  .
.

Dado que conocemos ya dos de los tres ángulo, podemos calcular el faltante,  , de manera directa
, de manera directa
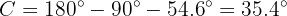
Para obtener el lado  aplicaremos tangente sobre el ángulo
aplicaremos tangente sobre el ángulo  y despejaremos
y despejaremos  :
:
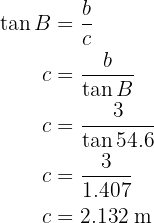
Para obtener el lado  aplicaremos seno sobre el ángulo
aplicaremos seno sobre el ángulo  y despejaremos
y despejaremos  :
:
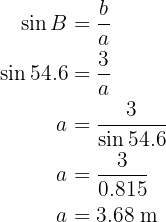
Hemos encontrados los lados y ángulos faltantes.
De un triángulo rectángulo  , se conoce la hipotenusa y un cateto
, se conoce la hipotenusa y un cateto 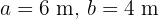 . Resolver el triángulo.
. Resolver el triángulo.
Obtengamos los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo, ya conocemos de antemano el ángulo  .
.
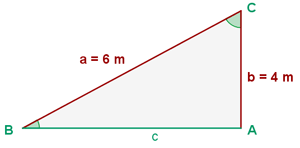
Para obtener el ángulo  primero calcularemos el coseno del ángulo utilizando el cateto y la hipotenusa que conocemos para posteriormente aplicar la función inversa arcocoseno.
primero calcularemos el coseno del ángulo utilizando el cateto y la hipotenusa que conocemos para posteriormente aplicar la función inversa arcocoseno.
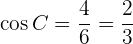
Aplicando arcocoseno obtenemos  . Notemos que, ahora que tenemos dos de los tres ángulo, podemos calcular de forma directa el ángulo faltante
. Notemos que, ahora que tenemos dos de los tres ángulo, podemos calcular de forma directa el ángulo faltante

Para obtener el lado  aplicaremos seno sobre el ángulo
aplicaremos seno sobre el ángulo  y despejaremos
y despejaremos  :
:
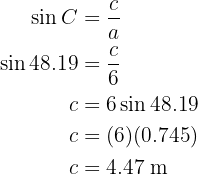
Hemos encontrados los lados y ángulos faltantes.
De un triángulo rectángulo  , se conocen los dos catetos
, se conocen los dos catetos 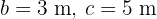 . Resolver el triángulo.
. Resolver el triángulo.
Obtengamos los lados y ángulos faltantes. Notemos que al ser un ángulo rectángulo, ya conocemos de antemano el ángulo  .
.
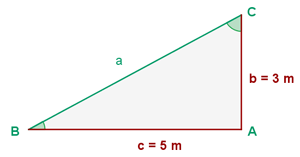
Para obtener el ángulo  primero calcularemos su tangente utilizando los catetos y posteriormente calcularemos el arcotangente
primero calcularemos su tangente utilizando los catetos y posteriormente calcularemos el arcotangente
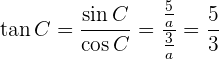
Así, tenemos que  . Ahora que tenemos dos de los tres ángulo podemos obtener el faltante de forma directa
. Ahora que tenemos dos de los tres ángulo podemos obtener el faltante de forma directa
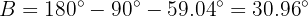
Para obtener el lado  aplicaremos seno sobre el ángulo
aplicaremos seno sobre el ángulo  y despejaremos
y despejaremos  :
:
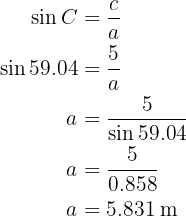
Hemos encontrados los lados y ángulos faltantes.
De un triángulo rectángulo  , se tiene la siguiente información: la hipotenusa es
, se tiene la siguiente información: la hipotenusa es 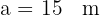 y
y 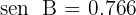 . Resolver el triángulo.
. Resolver el triángulo.
Notemos que al ser un triángulo rectángulo, sabemos que el ángulo  .
.

Aplicando arcoseno tenemos que
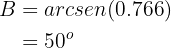
Ahora, una vez que tenemos dos ángulo, podemos calcular de manera inmediata el último;
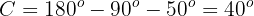
Aplicando coseno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
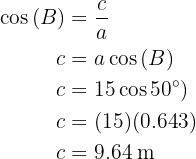
Aplicando seno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
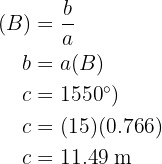
Así ya obtuvimos los datos faltantes.
De un triángulo rectángulo  , se tiene la siguiente información: la hipotenusa es
, se tiene la siguiente información: la hipotenusa es 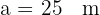 y
y 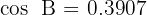 . Resolver el triángulo.
. Resolver el triángulo.
Notemos que al ser un triángulo rectángulo, sabemos que el ángulo  .
.

Aplicando arcocoseno tenemos que
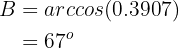
Ahora, una vez que tenemos dos ángulo, podemos calcular de manera inmediata el último;
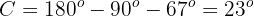
Aplicando coseno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
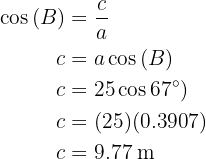
Aplicando seno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
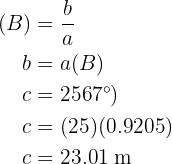
Así ya obtuvimos los datos faltantes.
De un triángulo rectángulo  , se tiene la siguiente información: la hipotenusa es
, se tiene la siguiente información: la hipotenusa es 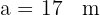 y
y 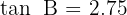 . Resolver el triángulo.
. Resolver el triángulo.
Notemos que al ser un triángulo rectángulo, sabemos que el ángulo  .
.

Aplicando arcotangente tenemos que
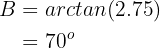
Ahora, una vez que tenemos dos ángulo, podemos calcular de manera inmediata el último;
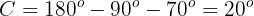
Aplicando coseno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
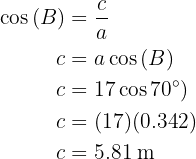
Aplicando seno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
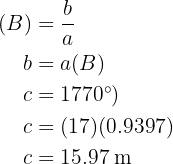
Así ya obtuvimos los datos faltantes.
De un triángulo rectángulo  , se tiene la siguiente información: la hipotenusa es
, se tiene la siguiente información: la hipotenusa es 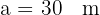 y
y 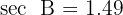 . Resolver el triángulo.
. Resolver el triángulo.
Notemos que al ser un triángulo rectángulo, sabemos que el ángulo  .
.

Aplicando arcosecante tenemos que
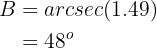
Ahora, una vez que tenemos dos ángulo, podemos calcular de manera inmediata el último;
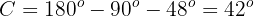
Aplicando coseno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
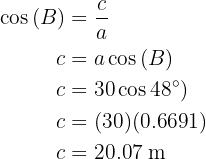
Aplicando seno en el ángulo  y despejando obtendremos el valor del lado
y despejando obtendremos el valor del lado  :
:
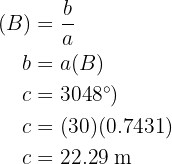
Así ya obtuvimos los datos faltantes.
Un árbol de  de alto proyecta una sombra de
de alto proyecta una sombra de  de larga. Encontrar el ángulo de elevación del sol en ese momento.
de larga. Encontrar el ángulo de elevación del sol en ese momento.
Observemos que entre el suelo y el árbol se forma un ángulo de  . Así, tenemos dos catetos. Además, tenemos que el ángulo de elevación es el ángulo formado en el vértice donde termina la sombra como se ve en la siguiente imagen
. Así, tenemos dos catetos. Además, tenemos que el ángulo de elevación es el ángulo formado en el vértice donde termina la sombra como se ve en la siguiente imagen
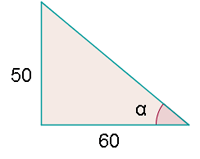
Por lo tanto, para obtener nuestro ángulo de elevación  primero calcularemos su tangente utilizando los catetos y posteriormente aplicaremos arcotangente a nuestro resultado
primero calcularemos su tangente utilizando los catetos y posteriormente aplicaremos arcotangente a nuestro resultado
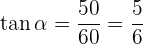
Por lo tanto, tenemos que  .
.
Un dirigible que está volando a 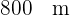 de altura, distingue un pueblo con un ángulo de depresión de
de altura, distingue un pueblo con un ángulo de depresión de 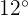 . ¿A qué distancia del pueblo se halla?
. ¿A qué distancia del pueblo se halla?
Tenemos que los datos proporcionados nos dan el esquema mostrado en la siguiente imagen.

Notemos que lo queremos en realidad es encontrar la distancia que debe recorrer el dirigible para volando sobre el pueblo. Esto es, queremos encontrar el cateto  , para esto calcularemos la tangente del ángulo con valor
, para esto calcularemos la tangente del ángulo con valor 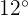 y a la vez utilizaremos los catetos y de ahí despejaremos
y a la vez utilizaremos los catetos y de ahí despejaremos  :
:
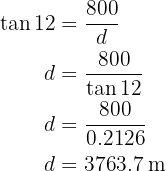
Hallar el radio de una circunferencia sabiendo que una cuerda de  tiene como arco correspondiente uno de
tiene como arco correspondiente uno de  .
.
Recordemos que el ángulo central mide lo mismo que el arco que lo abarca. Dicho lo anterior tenemos el siguiente esquema

Para obtener el radio (lado 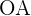 ) aplicaremos seno sobre el ángulo que mide
) aplicaremos seno sobre el ángulo que mide  utilizando el cateto que conocemos y
utilizando el cateto que conocemos y  para posteriormente despejar el radio:
para posteriormente despejar el radio:
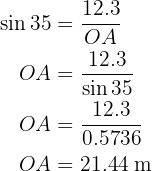
Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 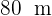 y
y 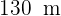 , y forman entre ellos un ángulo de
, y forman entre ellos un ángulo de  .
.
Obtengamos es el ángulo 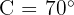 . Ahora, en la siguiente imagen mostramos el triángulo.
. Ahora, en la siguiente imagen mostramos el triángulo.

Notemos que la altura divide nuestro triángulo inicial en dos triángulos rectángulo. Utilizaremos el triángulo de la derecha, ya que tenemos más información en él, para obtener el valor de la altura y posteriormente calcular el área. Para obtener la altura utilizaremos el seno del ángulo  , el cateto que pertenece a este triángulo y la altura, así terminaremos despejando la altura:
, el cateto que pertenece a este triángulo y la altura, así terminaremos despejando la altura:
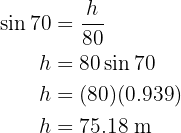
Ahora que sabemos que la altura mide 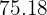 , calcularemos el área:
, calcularemos el área:
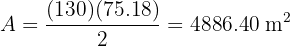
Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de  y si nos acercamos
y si nos acercamos  , bajo un ángulo de
, bajo un ángulo de 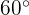 .
.
Primero intentemos ilustrar el problema para entender poder entenderlo mejor. La siguiente imagen nos ayudará con eso

Para resolver el problema, primero calcularemos la tangente del ángulo de  y sus catetos correspondientes y luego calcularemos la tangente del ángulo de
y sus catetos correspondientes y luego calcularemos la tangente del ángulo de 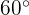 con sus catetos correspondientes y despejaremos
con sus catetos correspondientes y despejaremos  de ambos:
de ambos:
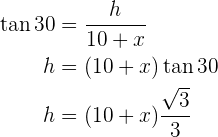
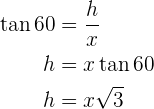
Notemos que esto nos dará un sistema de ecuaciones que solucionaremos la altura
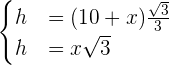
Resolviendo el sistema tenemos que 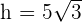 .
.
La longitud del lado de un octógono regular es  . Hallar los radios de la circunferencia inscrita y circunscrita.
. Hallar los radios de la circunferencia inscrita y circunscrita.
La siguiente imagen nos permite observar cuál es el radio de la circunferencia inscrita y cuál de la circunferencia circunscrita.

Notemos que el lado  . Además, el lado
. Además, el lado 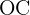 define el radio de la circunferencia inscrita, mientras que el lado
define el radio de la circunferencia inscrita, mientras que el lado 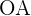 define el radio de la circunferencia circunscrita. Además, sabemos que el ángulo
define el radio de la circunferencia circunscrita. Además, sabemos que el ángulo  ya que se trata de un octágono, por lo tanto, tenemos que
ya que se trata de un octágono, por lo tanto, tenemos que  .
.
Radio de la circunferencia inscrita
Calcularemos la tangente del ángulo 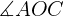 utilizando tanto el valor del ángulo como los catetos para, al final, poder despejar el cateto
utilizando tanto el valor del ángulo como los catetos para, al final, poder despejar el cateto 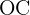 .
.
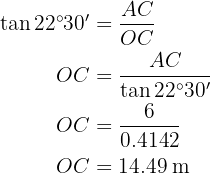
Radio de la circunferencia circunscrita
Calcularemos el seno del ángulo 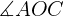 utilizando tanto el valor del ángulo como el cateto y la hipotenusa para, al final, poder despejar la hipotenusa
utilizando tanto el valor del ángulo como el cateto y la hipotenusa para, al final, poder despejar la hipotenusa 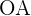 .
.
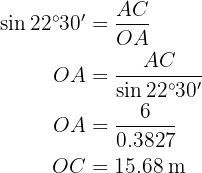
Calcular la longitud del lado y de la apotema de un octógono regular inscrito en una circunferencia de 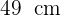 de radio.
de radio.
La siguiente imagen nos permite observar mejor el problema.

Notemos que el radio es igual al lado 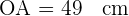 . Ahora, el lado del octógono está definido por
. Ahora, el lado del octógono está definido por  y que
y que 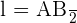 .
.
También notemos que el apotema 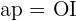 parte el ángulo
parte el ángulo  en dos. Además, sabemos que el ángulo
en dos. Además, sabemos que el ángulo  ya que se trata de un octágono, por lo tanto, tenemos que
ya que se trata de un octágono, por lo tanto, tenemos que 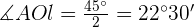 . Observemos además que los lados
. Observemos además que los lados 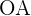 ,
,  y
y 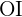 forman un triángulo rectángulo.
forman un triángulo rectángulo.
Lado del octógono
Calcularemos seno del ángulo 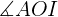 utilizando tanto el valor del ángulo como la hipotenusa (el radio del octógono) y el cateto (la mitad del lado del octógono) para, al final, poder despejar el cateto
utilizando tanto el valor del ángulo como la hipotenusa (el radio del octógono) y el cateto (la mitad del lado del octógono) para, al final, poder despejar el cateto  .
.
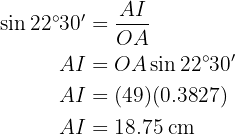
Por lo tanto, el lado mide 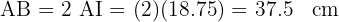 .
.
Apotema del octógono
Calcularemos coseno del ángulo 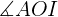 utilizando tanto el valor del ángulo como la hipotenusa (el radio del octógono) y el cateto (el apotema) para, al final, poder despejar el cateto
utilizando tanto el valor del ángulo como la hipotenusa (el radio del octógono) y el cateto (el apotema) para, al final, poder despejar el cateto 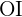 .
.
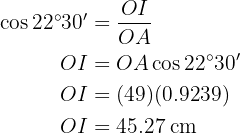
Tres pueblos  ,
,  y
y  están unidos por carreteras. La distancia de
están unidos por carreteras. La distancia de  a
a  es
es 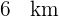 y la de
y la de  a
a  de
de 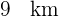 . Además, el ángulo que forman estas carreteras es de
. Además, el ángulo que forman estas carreteras es de 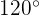 . ¿Cuánto distan
. ¿Cuánto distan  y
y  ?
?
La siguiente imagen nos permite observar mejor el problema.
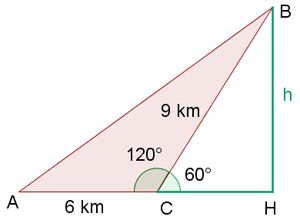
Notemos que hemos hecho unas construcciones adicionales para poder resolver el problema utilizando triángulos rectángulo. Para poder resolver el problema, debemos encontrar primero los catetos del triángulo rectángulo que hemos formado (el de color verde) y así, posteriormente, utilizaremos estos datos para poder obtener los catetos del triángulo más grande y, por lo tanto, de la hipotenusa, que es el valor que buscamos.
Catetos del triángulo rectángulo verde
Calcularemos el seno y el coseno del ángulo 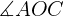 utilizando tanto el valor del ángulo como los catetos y la hipotenusa para, al final, poder despejar los catetos
utilizando tanto el valor del ángulo como los catetos y la hipotenusa para, al final, poder despejar los catetos  y
y  , respectivamente.
, respectivamente.

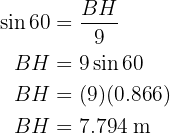
Catetos del triángulo rectángulo más grande e hipotenusa
Utilizaremos el teorema de pitágoras para calcular la hipotenusa. Primero, notemos que los catetos que utilizaremos serán  y
y 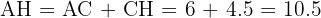 .
.

Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cálculo el lado bc aplicando la ley de cosenos b=5cm c=6cm a=60°
Materia:
erica V= 1
Calcula el lado BC aplicando
5
V
0
V
4
V
A
B
AB = 6cm
CR
Datos
0 =5cm
C=600
En un triángulo, se tienen los datos: A = 50° ,B = 65° y a = 12. Encuentra el lado b.
excelente, por ejemplo tengo uno donde me hacen falta el ángulo A, B, C tengo estos datos lado a:14, b:6, c:4
La respuesta es 14.197
¿ porqué no hay un modo de resolver triángulos sin la necesidad de aplicar la Trigonometria académica ? Saludos, profesor.
Hola, posiblemente exista otro método, pero por desgracia es todavía mas difícil que la trigonometría académica incluso te puedo asegurar que hoy en día es mas fácil y mas directo resolver los problemas de triángulos, entendemos que a veces llega a ser confuso pero te aseguramos que este método es el mas sencillo que existe.
Resuelve esto bien y claro.
¿Cuánto le falta al complemento del suplemento de 165,315° para alcanzar el suplemento del complemento de π/12 rad?
como resolver este ejercicio (tag x )2 -1
_________= -(tag x )2
(cotag x )2 -1