Los triángulos oblicuángulos son aquellos que no tienen ningún ángulo recto, lo que los hace especialmente interesantes y desafiantes de trabajar. En este conjunto de ejercicios, exploraremos las propiedades y relaciones de estos triángulos únicos.
Durante este recorrido, aprenderás a calcular los lados y ángulos desconocidos utilizando diferentes métodos, como la ley de los senos, la ley de los cosenos y la aplicación de las razones trigonométricas. Estas herramientas matemáticas te permitirán resolver una amplia variedad de problemas del mundo real, desde la medición de distancias inaccesibles hasta la determinación de alturas y ángulos en terrenos irregulares.
Además, te enfrentarás a desafíos que involucran resolución de problemas y aplicaciones prácticas de los triángulos oblicuángulos en situaciones cotidianas y en diversas disciplinas, como la navegación, la arquitectura, la astronomía y más.
De un triángulo sabemos que:  ,
,  y
y  . Calcula los restantes elementos.
. Calcula los restantes elementos.
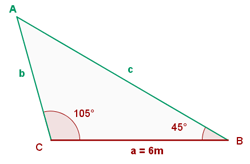
1 Como la suma de los tres ángulos de un triángulo es  , podemos calcular fácilmente el ángulo
, podemos calcular fácilmente el ángulo  :
:

2 Aplicamos la ley de senos para calcular los lados  y
y  :
: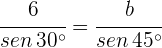
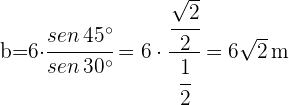
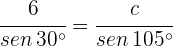

De un triángulo sabemos que:  ,
,  y
y  . Calcula los restantes elementos
. Calcula los restantes elementos
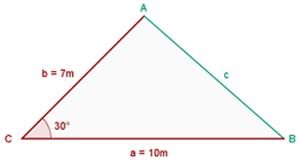
1 Aplicamos la ley de cosenos para calcular el lado  :
:
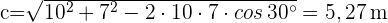
2 Aplicamos ley de senos para calcular el ángulo  :
:
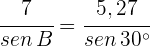
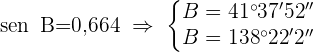
 ya que al ser
ya que al ser  , el ángulo obtuso será
, el ángulo obtuso será  .
.
3 Para calcular el ángulo  verificamos que sumen
verificamos que sumen  :
: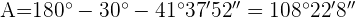
De un triángulo sabemos que:  . Calcula los restantes elementos.
. Calcula los restantes elementos.
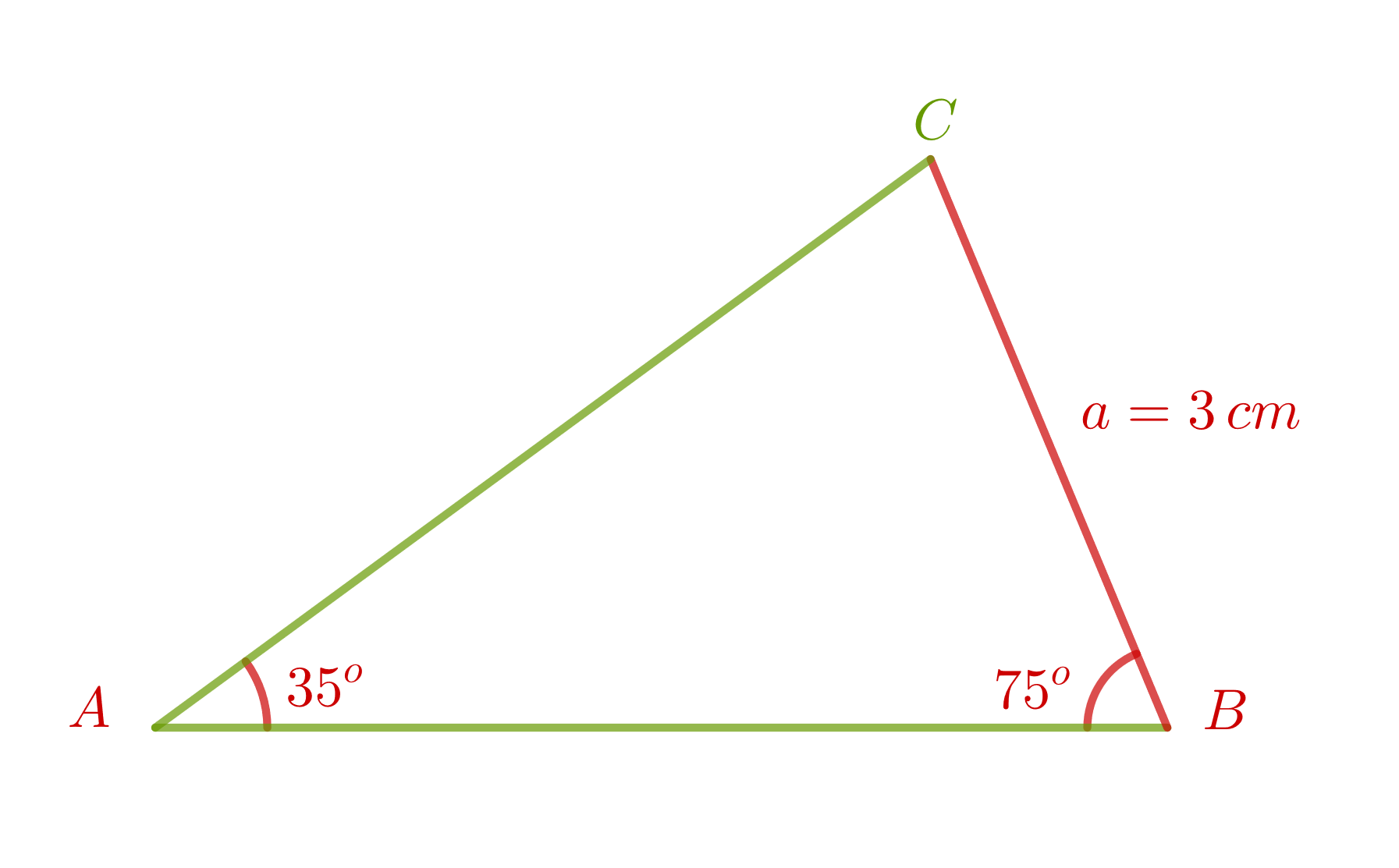
1 Como la suma de los tres ángulos de un triángulo es 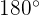 , podemos calcular fácilmente el ángulo
, podemos calcular fácilmente el ángulo  :
: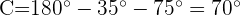
2 Aplicamos la ley de senos para calcular el lado  :
:
3 Aplicamos ley de senos para calcular el lado  :
: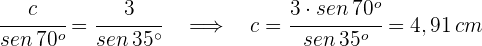
Resuelve el triángulo de datos: 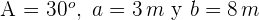 .
.
1 Aplicamos la ley de senos con los datos dados

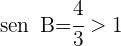
2 Como el seno de un ángulo nunca puede ser mayor que  , el problema no tiene solución. La figura muestra la imposibilidad de que exista el triángulo planteado.
, el problema no tiene solución. La figura muestra la imposibilidad de que exista el triángulo planteado.

Resuelve el triángulo de datos: 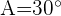 ,
, 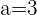 m y
m y 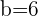 m.
m.
1 Aplicamos la ley de senos para calcular el ángulo  :
:
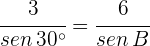
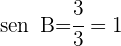
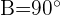
2 Como 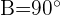 , es un triángulo rectángulo, podemos calcular el ángulo
, es un triángulo rectángulo, podemos calcular el ángulo  considerando que los ángulos agudos deben sumar
considerando que los ángulos agudos deben sumar  :
:
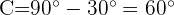
3 Calculamos el lado  aplicando funciones trigonométricas:
aplicando funciones trigonométricas:

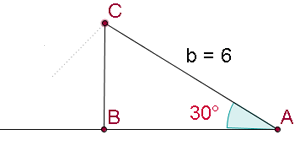
Resuelve el triángulo de datos: 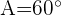 ,
,  m y
m y  m.
m.
1 Aplicamos ley de senos para calcular el ángulo 

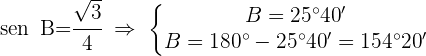
2 Como 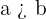 , sólo es válida la solución:
, sólo es válida la solución: 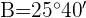
3 Calculamos el ángulo  considerando que los 3 ángulos deben sumar
considerando que los 3 ángulos deben sumar  :
:
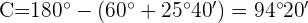
4 Calculamos el lado  aplicando la ley de senos:
aplicando la ley de senos:

 m
m
Resuelve el triángulo de datos: 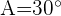 ,
,  y
y 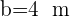 .
.
1 Aplicamos ley de senos para calcular el ángulo  :
:
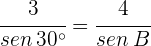
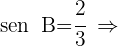

2 Como  son válidas las dos soluciones
son válidas las dos soluciones
3 Calculamos el ángulo  y el lado
y el lado  para el valor de
para el valor de 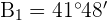
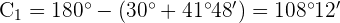

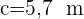
4 Calculamos el ángulo  y el lado
y el lado  para el valor de
para el valor de 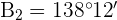
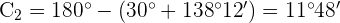
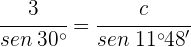
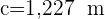
Resuelve el triángulo de datos:  ,
, 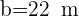 y
y 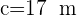
1 Aplicamos la ley de cosenos para calcular los ángulos  y
y 
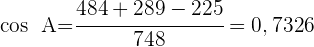
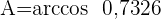
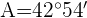
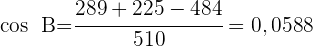
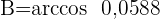

2 Calculamos el ángulo  considerando que los tres ángulos suman
considerando que los tres ángulos suman 
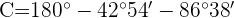
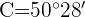
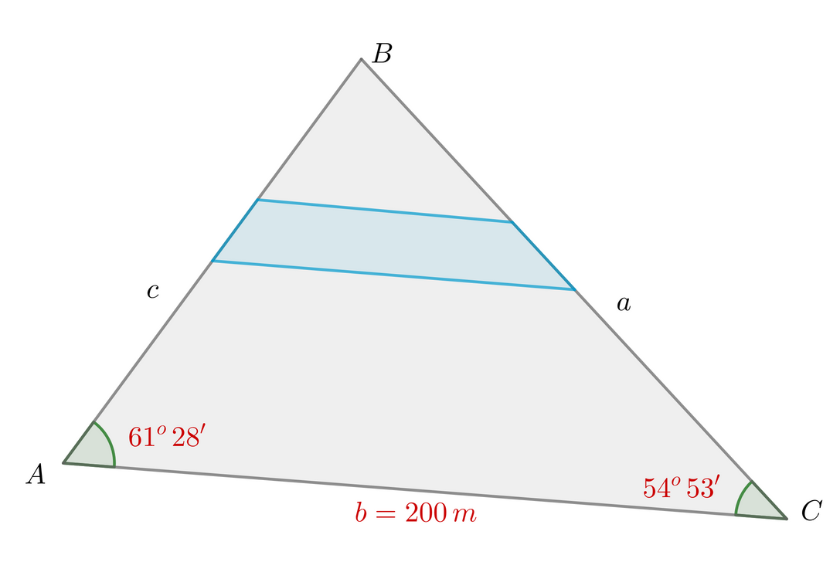
Calcula la altura,  , de la figura:
, de la figura:
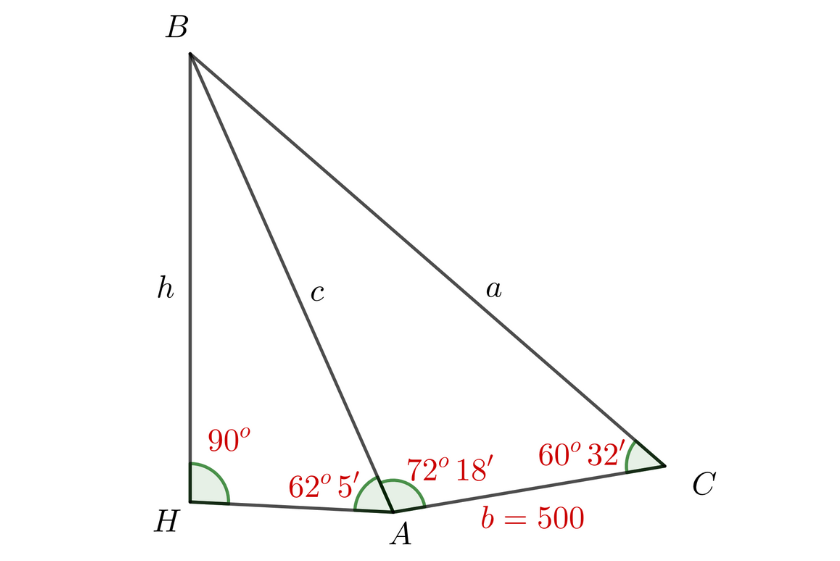
1 Como conocemos 2 ángulos del triángulo  , podemos calcular el
, podemos calcular el  considerando que la suma de los tres ángulos debe ser
considerando que la suma de los tres ángulos debe ser 
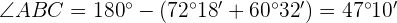
2 Aplicamos la ley de senos para calcular el lado  :
:
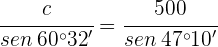
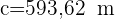
3 Como el triángulo  es rectángulo, aplicamos funciones trigonométricas para calcular el lado
es rectángulo, aplicamos funciones trigonométricas para calcular el lado  :
:
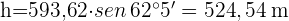
Calcula la distancia que separa el punto  del punto inaccesible
del punto inaccesible 
1 Calculamos el ángulo  considerando que la suma de los tres ángulos es
considerando que la suma de los tres ángulos es  :
:
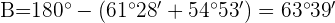
2 Aplicamos la ley de senos para calcular el lado  :
:
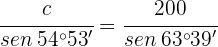
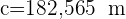
Calcula la distancia que separa entre dos puntos inaccesibles  y
y 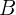

1 Considerando el triángulo 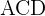 , aplicamos la ley de senos para calcular
, aplicamos la ley de senos para calcular 

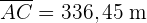
2 Considerando el triángulo 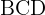 , aplicamos ley de senos para calcular
, aplicamos ley de senos para calcular 


3 Aplicamos ley de cosenos para calcular la distancia 


Calcular el radio del círculo circunscrito en un triángulo, donde 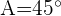 ,
,  y
y 
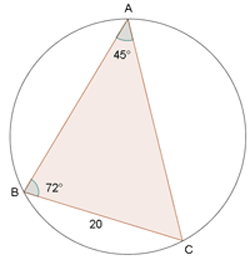
1 Considerando que 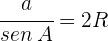

El radio de una circunferencia mide  m. Calcula el ángulo que formarán las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de longitud
m. Calcula el ángulo que formarán las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de longitud  m.
m.
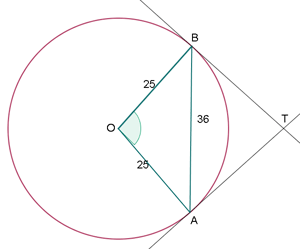
1 Aplicamos la ley de cosenos para calcular el ángulo 
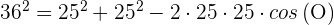

2 En el cuadrilátero 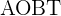 , los ángulos
, los ángulos  y
y  son rectos.
son rectos.
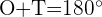

Las diagonales de un paralelogramo miden  cm y
cm y  cm, y el ángulo que forman es de
cm, y el ángulo que forman es de  . Calcular los lados.
. Calcular los lados.

1 Calculamos 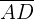 aplicando la ley de cosenos
aplicando la ley de cosenos
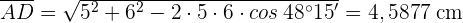
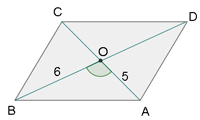
2 Calculamos el 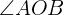 considerando que es suplementario al
considerando que es suplementario al 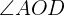 :
:

3 Aplicamos la ley de cosenos para calcular 
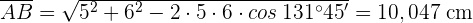
Dos personas se encuentran alineadas con un edificio y del mismo lado. Si las personas se encuentran separadas 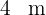 entre si y los ángulos de elevación para observar la parte más alta del edificio son
entre si y los ángulos de elevación para observar la parte más alta del edificio son 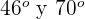 respectivamente. Calcular la altura del edificio.
respectivamente. Calcular la altura del edificio.
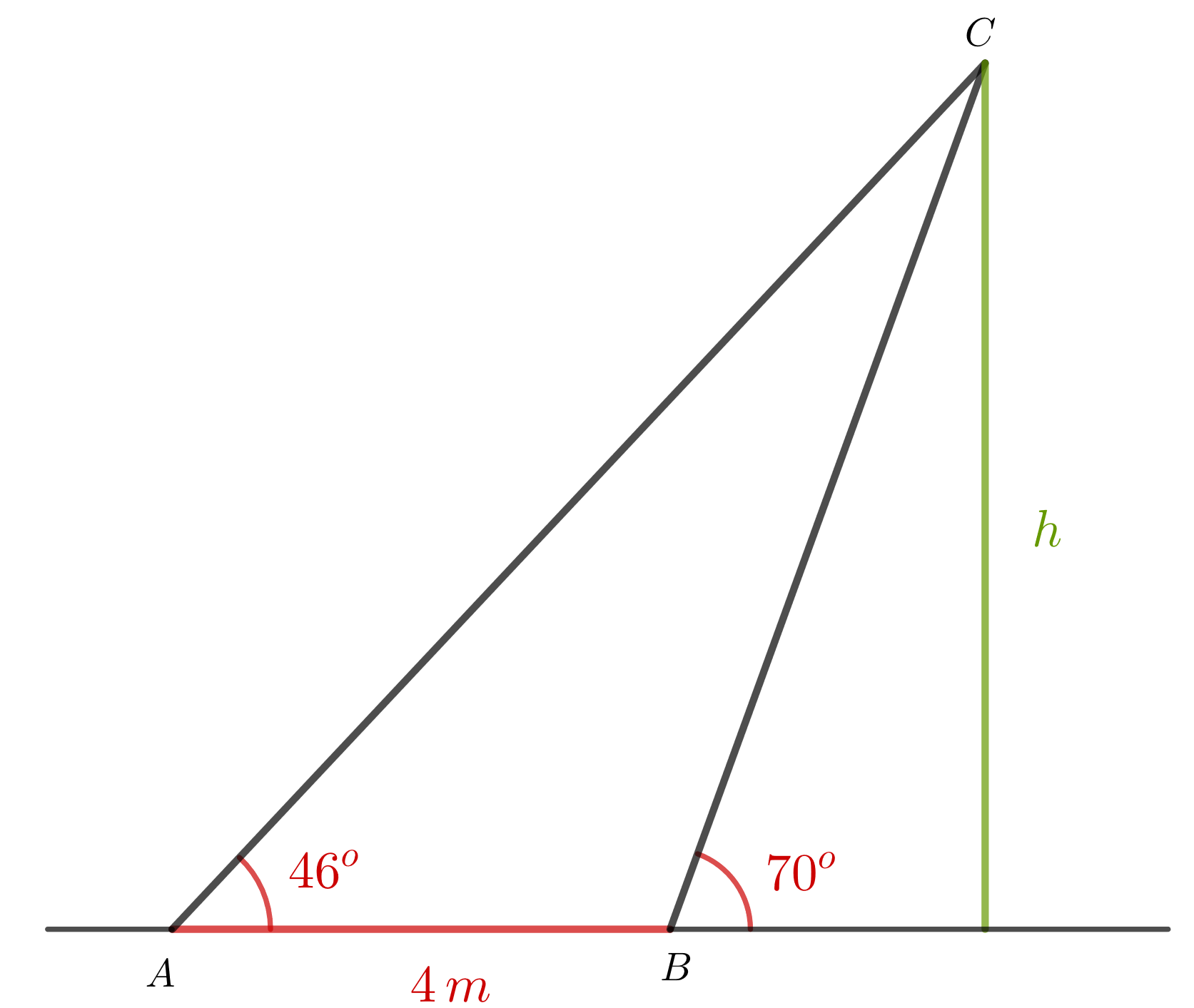
1 Calculamos el ángulo  sabiendo que es el suplemento de
sabiendo que es el suplemento de 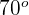 ; así,
; así, 
2 Calculamos el ángulo 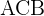 sabiendo que la suma de los ángulos interiores de un triángulo es
sabiendo que la suma de los ángulos interiores de un triángulo es 

3 Calculamos el lado  aplicando la ley de los senos:
aplicando la ley de los senos:
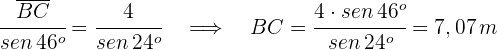
4 Calculamos la altura a partir del seno de 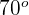

Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cálculo el lado bc aplicando la ley de cosenos b=5cm c=6cm a=60°
Materia:
erica V= 1
Calcula el lado BC aplicando
5
V
0
V
4
V
A
B
AB = 6cm
CR
Datos
0 =5cm
C=600
En un triángulo, se tienen los datos: A = 50° ,B = 65° y a = 12. Encuentra el lado b.
excelente, por ejemplo tengo uno donde me hacen falta el ángulo A, B, C tengo estos datos lado a:14, b:6, c:4
La respuesta es 14.197
¿ porqué no hay un modo de resolver triángulos sin la necesidad de aplicar la Trigonometria académica ? Saludos, profesor.
Hola, posiblemente exista otro método, pero por desgracia es todavía mas difícil que la trigonometría académica incluso te puedo asegurar que hoy en día es mas fácil y mas directo resolver los problemas de triángulos, entendemos que a veces llega a ser confuso pero te aseguramos que este método es el mas sencillo que existe.
Resuelve esto bien y claro.
¿Cuánto le falta al complemento del suplemento de 165,315° para alcanzar el suplemento del complemento de π/12 rad?
como resolver este ejercicio (tag x )2 -1
_________= -(tag x )2
(cotag x )2 -1