Hallar las ecuaciones de los ejes coordenados y de los planos coordenados
Eje 
1El eje  pasa por el punto
pasa por el punto 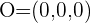 y tiene la dirección
y tiene la dirección 
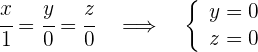
2Eje 
El eje  pasa por el punto
pasa por el punto 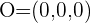 y tiene la dirección
y tiene la dirección 
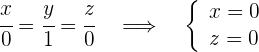
3Eje 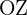
El eje  pasa por el punto
pasa por el punto 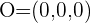 y tiene la dirección
y tiene la dirección 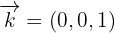
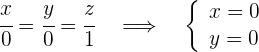
4Plano 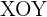
El plano 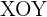 pasa por el punto
pasa por el punto 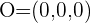 y contiene los vectores
y contiene los vectores 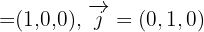
Aplicamos la ecuación del plano

5Plano 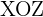
El plano 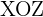 pasa por el punto
pasa por el punto 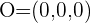 y contiene los vectores
y contiene los vectores 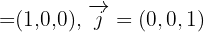
Aplicamos la ecuación del plano
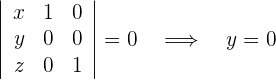
6Plano 
El plano  pasa por el punto
pasa por el punto 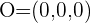 y contiene los vectores
y contiene los vectores 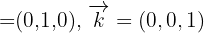
Aplicamos la ecuación del plano

Hallar la ecuación del plano que contiene a las rectas:
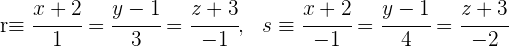
1Ambas rectas pasan por el punto 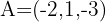 , por lo que este punto se encuentra en el plano
, por lo que este punto se encuentra en el plano
2El plano contiene a los vectores de dirección de ambas rectas, estos son

3Aplicamos la ecuación del plano

Hallar la ecuación del plano que contiene al punto  y a la recta:
y a la recta:

1La rectas pasa por el punto  , por lo que este punto se encuentra en el plano
, por lo que este punto se encuentra en el plano
2El plano contiene al vector de dirección
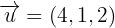
3El plano contiene al vector
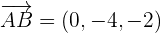
4Aplicamos la ecuación del plano

Hallar las coordenadas del punto común al plano 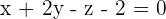 y a la recta determinada por el punto
y a la recta determinada por el punto 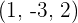 y el vector
y el vector

1La ecuación paramétrica de la recta es

2Sustituimos  en la ecuación del plano
en la ecuación del plano

3Resolviendo se obtiene
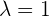
4Así, el punto común buscado es 
Hallar la ecuación segmentaria del plano que pasa por los puntos

1La ecuación segmentaria de la recta es

Sea  un plano que pasa por
un plano que pasa por  y corta a los semiejes coordenados positivos en los puntos
y corta a los semiejes coordenados positivos en los puntos  . Sabiendo que el triángulo
. Sabiendo que el triángulo  es equilátero, hallar las ecuaciones de
es equilátero, hallar las ecuaciones de

1La ecuación segmentaria de la recta es
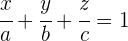
2Como el triángulo es equilátero, sus segmentos son iguales

3Sustituyendo el punto  se obtiene
se obtiene

4Así, la ecuación del plano es 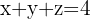
Hallar la ecuación del plano que pasa por el punto  y es paralelo a la recta:
y es paralelo a la recta:
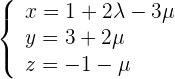
1El punto  se encuentra en el plano
se encuentra en el plano
2El plano contiene a los vectores de dirección
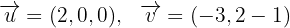
3Aplicamos la ecuación del plano

Hallar la ecuación del plano que contiene a la recta 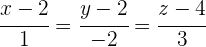 y es paralelo a la recta:
y es paralelo a la recta:

1El punto  se encuentra en el plano
se encuentra en el plano
2El plano contiene al vector de dirección
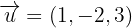
3El vector  es un vector del plano, por ser paralelo a la recta
es un vector del plano, por ser paralelo a la recta
4Aplicamos la ecuación del plano

Hallar la ecuación del plano que pasa por el punto  y es paralelo a las rectas:
y es paralelo a las rectas:
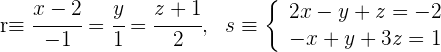
1Pasamos la recta  a su forma paramétrica, para esto la escribimos en términos de
a su forma paramétrica, para esto la escribimos en términos de 

Calculamos las coordenadas
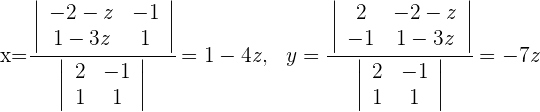
Obtenemos

2El plano contiene a los vectores de dirección de ambas rectas, estos son
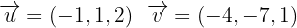
3Aplicamos la ecuación del plano
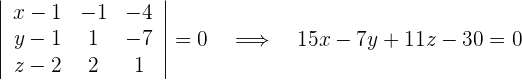
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Les felicito por su pedagogica web.
Podrian indicarme cual es la formula de las coordenadas del pie de una perpendicular por un punto (X1,Y1) a una recta Ax+By+c=0
Serian tan amables de enviarme dos formulas:
1) Formula de la pendiente de la bisectriz de 45º relacionada con las pendientes de los lados del angulo de 90º.
2) Formulas de las coordenadas del punto/pie de una perpendicular que pasa por el punto P(x0,y0) y una recta Ax+By+c=0.
Gracias de antemano.
M.Angel
En los ejercicios 7 y 8, trazar las rectas que pasan por el punto dado con la pendiente indicada. Dibujar en un mismo sistema de coordenadas.
Hola tu indicación es muy buena, vamos a ir mejorando para un mejor entendimiento.
Me puede ayudar con este problema
la pendiente de una recta que pasa por el punto A(3, 2) es igual a 3/4. situar dos puntos sobre esta recta que disten 5 unidades de A.
con su gráfica mas
Alguien me puede ayudar por favor necesito dar un examen para repasar y no me salen las respuestas
Hola con gusto te ayudamos, podrías mencionar específicamente con cual ejercicio podemos darte una mejor explicación.
Determinar las ecuaciones parametricas del plano x-2y+z-1=0
Hola, me sirvio mucho, con que informacion podria ponerlos como refernecia en mi proyecto?
Hola que bueno que la pagina te ayudo, podrías poner como pagina de internet «Materíal didactico-Superprof».