¡Bienvenidos a nuestra página donde las integrales y el cálculo de áreas cobran vida! Si alguna vez te has maravillado con la idea de medir superficies irregulares y curvas utilizando matemáticas avanzadas, estás en el lugar adecuado. En este espacio, exploraremos las herramientas poderosas que nos brindan las aplicaciones del cálculo integral para desentrañar los secretos de figuras geométricas complejas y sus áreas.
Desde áreas bajo curvas suaves, delimitadas por funciones, hasta superficies más intrincadas, te guiaremos a través de ejemplos prácticos y emocionantes para comprender cómo aplicar las integrales en el mundo real.
Prepárate para expandir tus horizontes matemáticos y desarrollar una nueva apreciación por la belleza y utilidad de las integrales. ¡Así que adelante, adéntrate en este emocionante mundo de áreas e integrales, y descubre cómo las matemáticas pueden revelar secretos sorprendentes! ¡Comencemos a calcular integrales y áreas juntos!
Hallar el área limitada por la recta  , el eje
, el eje  y las rectas
y las rectas  y
y 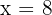 .
.
1Representamos gráficamente las rectas y el eje indicados; también ubicamos el área solicitada

2Los extremos del área solicitada están dados por las rectas  y
y 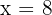 , por ello representamos la recta en función de la variable
, por ello representamos la recta en función de la variable 
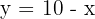
3El área solicitada viene dada por

4Sustituimos  en función de
en función de  y resolvemos la integral definida
y resolvemos la integral definida

Calcular el área del recinto limitado por la curva 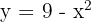 y el eje
y el eje  .
.
1Hallamos los puntos donde la curva corta al eje  , ya que estos serán los límites de integración; para esto igualamos la curva a cero y encontramos los valores de
, ya que estos serán los límites de integración; para esto igualamos la curva a cero y encontramos los valores de 
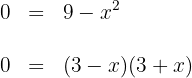
entonces 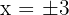 son los puntos donde la curva corta al eje
son los puntos donde la curva corta al eje  . La representación gráfica es
. La representación gráfica es

2El área solicitada viene dada por
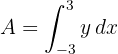
3Sustituimos  en función de
en función de  y resolvemos la integral definida
y resolvemos la integral definida

Como la parábola es simétrica respecto al eje 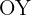 , el área será igual al doble del área comprendida entre
, el área será igual al doble del área comprendida entre  y
y 
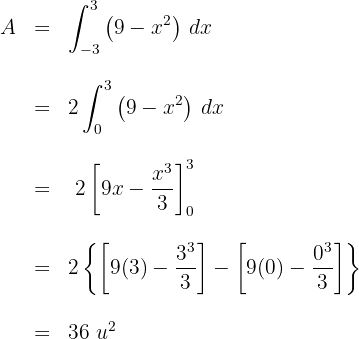
Calcular el área del triángulo de vértices 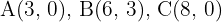 .
.
1Representamos gráficamente los puntos dados y ubicamos el área solicitada
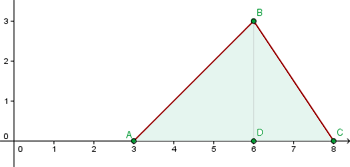
2Calculamos las pendientes de las rectas  y
y  y con ello las respectivas ecuaciones de las rectas
y con ello las respectivas ecuaciones de las rectas

3El área solicitada viene dada en dos partes, una para cada recta

4Sustituimos las rectas en función de  y resolvemos la integral definida
y resolvemos la integral definida
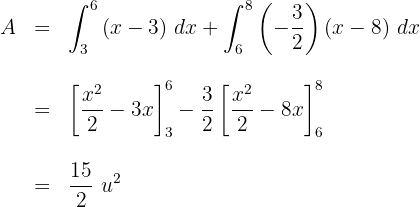
Calcular el área limitada por las gráficas de 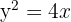 e
e  .
.
1Representamos gráficamente las curvas dadas e identificamos el área solicitada
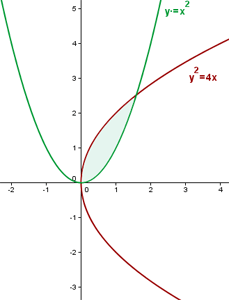
2Calculamos los límites de integración, para ello buscamos los puntos de intersección de las curvas
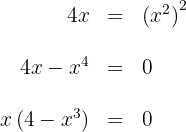
entonces,  y
y 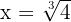 son los límites de integración.
son los límites de integración.
3El área solicitada viene dada por la integral de la diferencia de ambas curvas
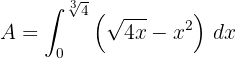
4Resolvemos la integral definida

Calcular el área limitada por la curva 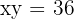 , el eje
, el eje  y las rectas
y las rectas  ,
,  .
.
1Representamos gráficamente las curvas dadas e identificamos el área solicitada
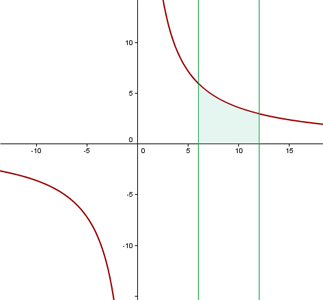
2El área solicitada viene dada por
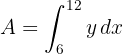
3Sustituimos  en función de
en función de  y resolvemos la integral definida
y resolvemos la integral definida
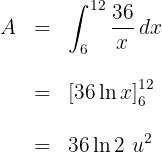
Calcular el área limitada por la curva 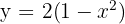 y la recta
y la recta 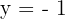 .
.
1Representamos gráficamente la curva y recta dadas e identificamos el área solicitada
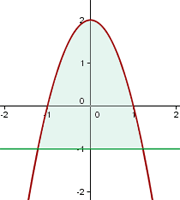
2Calculamos los límites de integración, para ello buscamos los puntos de intersección de las curvas
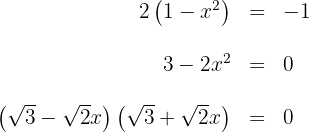
entonces,  son los límites de integración.
son los límites de integración.
3El área solicitada viene dada por la integral de la diferencia de ambas curvas
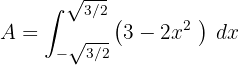
4Resolvemos la integral definida observando que el área es simétrica respecto al eje 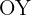

Calcular el área del recinto limitado por la parábola 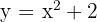 y la recta que pasa por los puntos
y la recta que pasa por los puntos  y
y 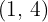 .
.
1Representamos gráficamente la curva y recta dadas e identificamos el área solicitada
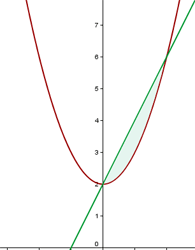
2Calculamos la pendiente de la recta y su respectiva ecuación
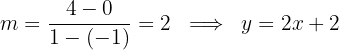
3Calculamos los límites de integración, para ello buscamos los puntos de intersección de las curvas
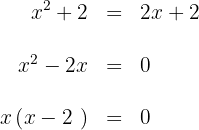
entonces,  y
y  son los límites de integración.
son los límites de integración.
4El área solicitada viene dada por la integral de la diferencia de ambas curvas

5Resolvemos la integral definida

Hallar el área limitada por las rectas 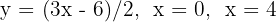 y el eje de abscisas.
y el eje de abscisas.
1Representamos gráficamente las rectas dadas e identificamos el área solicitada

2El área solicitada viene dada por la integral de la región bajo el eje  y la región por encima de dicho eje. La región bajo el eje tiene área negativa, por lo que consideramos su valor absoluto
y la región por encima de dicho eje. La región bajo el eje tiene área negativa, por lo que consideramos su valor absoluto
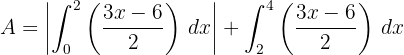
3Resolvemos la integral definida
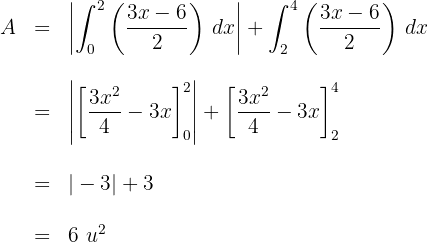
Calcular el área limitada por la curva 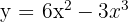 y el eje de abscisas.
y el eje de abscisas.
1Representamos gráficamente la curva dada e identificamos el área solicitada
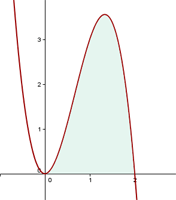
2Calculamos los límites de integración, para ello buscamos los puntos de intersección de la curva con el eje de las abcisas

entonces,  y
y  son los límites de integración.
son los límites de integración.
3El área solicitada viene dada por la integral

4Resolvemos la integral definida
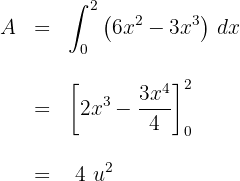
Hallar el área de la región del plano limitada por las curvas 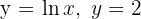 y los ejes coordenados.
y los ejes coordenados.
1Representamos gráficamente las curvas dadas e identificamos el área solicitada
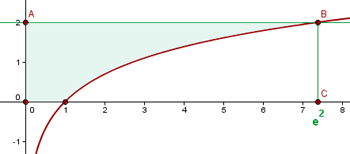
2El área solicitada viene dada por la integral

Observamos de la representación gráfica, que si integramos respecto a la variable  , el cálculo se simplifica, para esto expresamos la curva en función de
, el cálculo se simplifica, para esto expresamos la curva en función de  , esto es,
, esto es,
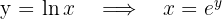
y el área solicitada se expresa
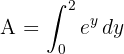
3Resolvemos la integral definida
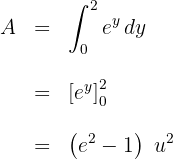
Calcular el área de la región del plano limitada por el círculo 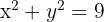 .
.
1Representamos gráficamente la curva dada. Observamos que el área solicitada es igual a cuatro veces el área que se encuentra en el primer cuadrante
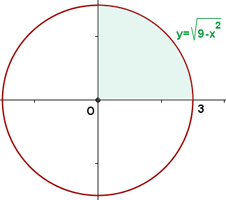
2Expresamos la parte del círculo que se encuentra en el primer cuadrante en función de 
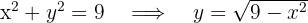
3El área solicitada viene dada por
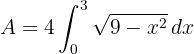
4Resolvemos la integral definida, para esto empleamos la sustitución trigonométrica 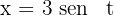 cuya diferencial es
cuya diferencial es 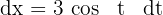 y tiene por límites de integración a
y tiene por límites de integración a
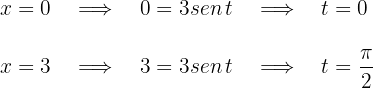
Sustituimos los valores de 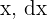 en términos de
en términos de 
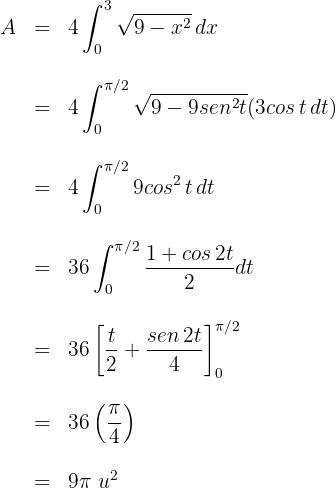
Hallar el área de una elipse de semiejes  y
y  .
.
1Representamos gráficamente la elipse centrada en el origen y con los semiejes dados
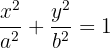
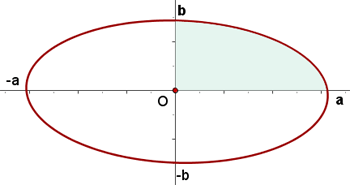
Observamos que el área solicitada es igual a cuatro veces el área que se encuentra en el primer cuadrante
2Expresamos la parte de la elipse que se encuentra en el primer cuadrante en función de 

3El área solicitada viene dada por

4Resolvemos la integral definida, para esto empleamos la sustitución trigonométrica  cuya diferencial es
cuya diferencial es  y tiene por límites de integración a
y tiene por límites de integración a

Sustituimos los valores de 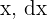 en términos de
en términos de 
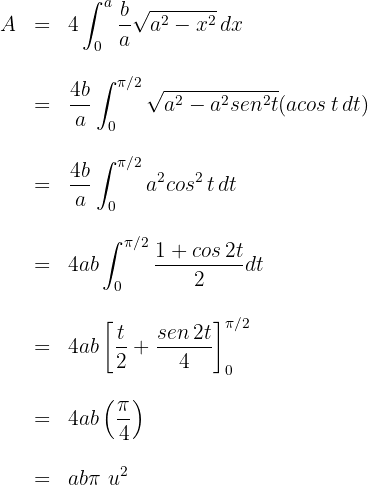
Calcular el área de la región del plano limitada por las raíces de la curva 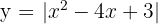 y el eje
y el eje  .
.
1Representamos analítica y gráficamente la curva y localizamos el área solicitada
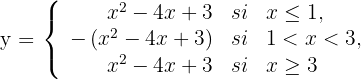
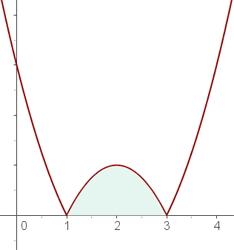
2Calculamos las raíces de la curva

entonces  y
y  son las raíces de la curva
son las raíces de la curva
3El área solicitada viene dada por
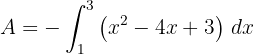
4Resolvemos la integral definida
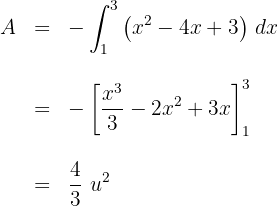
Hallar el área de la figura limitada por 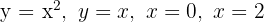 .
.
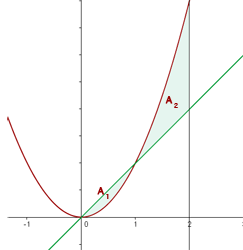
1Representamos analítica y gráficamente la curva y localizamos el área solicitada
2Calculamos la intersección de la recta y la parábola
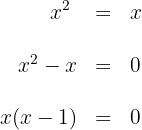
entonces  y
y  son las coordenadas de las abcisas donde se intersectan las dos curvas
son las coordenadas de las abcisas donde se intersectan las dos curvas
3El área solicitada viene dada en dos partes. En la primera la recta se encuentra por encima de la parábola y en la segunda la parábola se encuentra por encima de la recta

Así, el área solicitada viene dada por
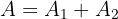
4Resolvemos las integrales definidas

Hallar el área del recinto plano y limitado por la parábola 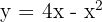 y las tangentes a la curva en los puntos de intersección con el eje
y las tangentes a la curva en los puntos de intersección con el eje  .
.
1Encontramos la intersección con el eje 
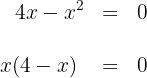
entonces  y
y  son las raíces, por los que los puntos de intersección son
son las raíces, por los que los puntos de intersección son 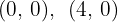 .
.
2Encontramos la ecuación de la recta tangente en 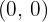

Encontramos la ecuación de la recta tangente en 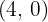

La intersección e ambas rectas se encuentra en 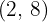
3Representamos gráficamente la curva con las tangentes indicadas y localizamos el área solicitada
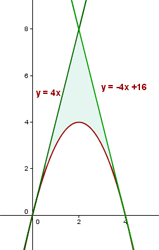
4El área solicitada viene dada por en dos partes. En la primera la recta con pendiente positiva se encuentra por encima de la parábola y en la segunda la recta con pendiente negativa se encuentra por encima de la parábola
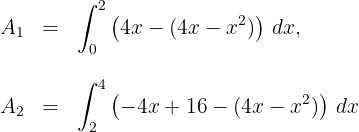
Así, el área solicitada viene dada por
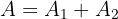
5Resolvemos las integrales definidas
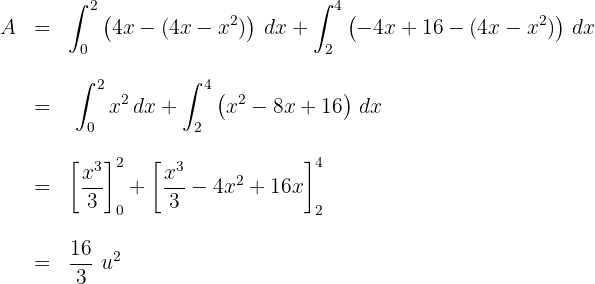
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
me puedes indicar por favor como desarrollar la integral e^x^2 sin (x) dx
Fe de erratas:
Ej. 3: sobra una raíz de x en el denominador antes del
Resultado final.
Ej.4: En el resultado final falta el signo menos.
Un saludo.
Hola revise los ejemplos de muchas ejercicios y no encontré los errores, podrías hacerme el favor de darme mas detalles para poder encontrarlos y quitar esos errores, seria de mucha ayuda.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))