¿Qué representa la integral definida y cómo la calculamos?
Recordemos que el Teorema Fundamental del Cálculo nos dice que la integral definida se puede calcular utilizando
donde 
es cualquier antiderivada de 
(o primitiva).
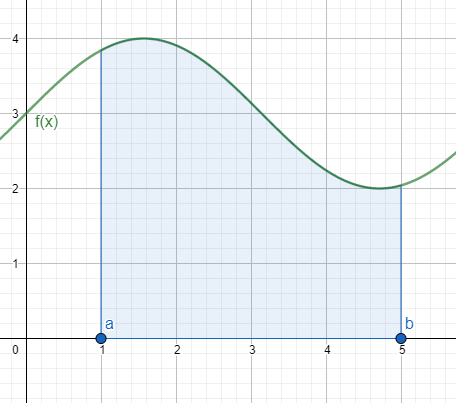
Además, recordemos que la integral definida mide el área debajo de la curva de entre los puntos 
y 
, tal y como se aprecia en la siguiente figura:
Ejercicios propuestos
Resuelve las siguientes integrales definidas:
1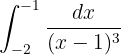 
La primera integral la podemos resolver con la fórmula para integrar una potencia. Notemos primero que
Por lo que podemos utilizar la fórmula
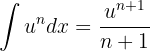
con el cambio de variable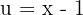 
y 
(notemos que en integrales definidas no es necesaria la constante de integración). De esta manera, obtenemos,
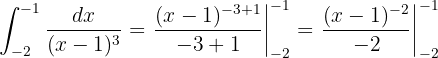
Es decir,
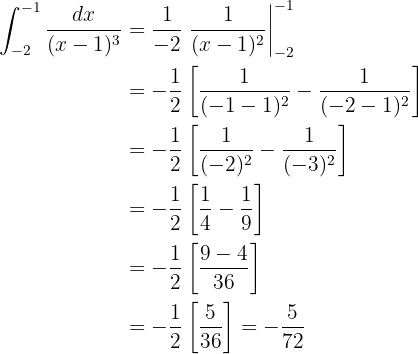
2 
Al igual que en el caso anterior, esta integral la resolvemos con la fórmula de la integral de una potencia:
simplificamos un poco,
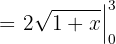
Y evaluamos en los límites de la integral:
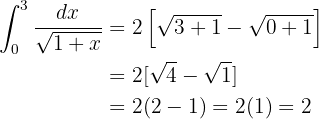
3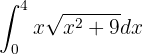 
Esta integral se resuelve con un cambio de variable. Notemos que dentro de la raíz tenemos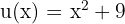 
. Si derivamos, tenemos 
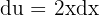; que al despejar 
, nos da
Además, como haremos cambio de variable, también debemos cambiar los límites de la integral. En particular,
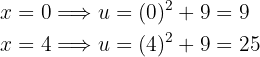
Por lo tanto, la integral se conviete en
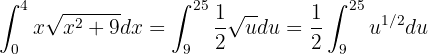
Ahora resolvemos la integral utilizando la fórmula de la integral de una potencia:
4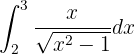 
Al igual que en el caso anterior, hacemos el siguiente cambio de variable
donde, al derivar, tenemos 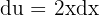. Por tanto, al despejar (ya que es lo que tenemos dentro del integrando), obtenemos
Ahora obtenemos los nuevos límites:
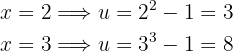
Por tanto, la integral se convierte en
Integramos con la fórmula de la integral de una potencia:
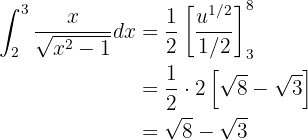
5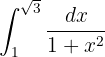 
Esta integral se resuelve muy rápido si recordamos que
Por lo que la integral se resuelve de inmediato:
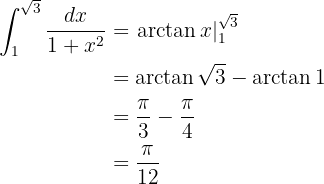
Recordemos que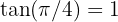 
y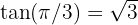 
(recordar esos valores es útil cuando deseamos encontrar los valores de la arco-tangente).
6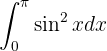 
Para resolver esta integral necesitamos una identidad trigonométrica. En particular, como tenemos a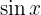 
elevado a una potencia par (2 en este caso), entonces necesitamos de alguna potencia que reduzca hasta alguna potencia impar. Esta la podemos obtener a partir de la identidad del ángulo doble para coseno:
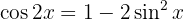
que, al despejar 
, obtenemos
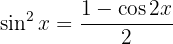
De esta forma, la integral se convierte en
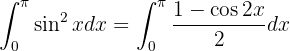
La cual ya se puede integrar de una forma más sencilla:
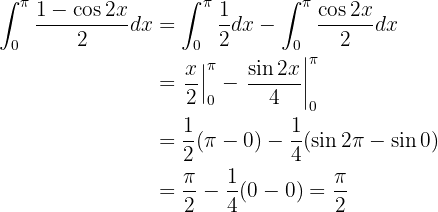
7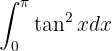 
Es un poco complicado encontrar —por medio de prueba y error— alguna función tal que 
). Por este motivo, es mejor transformar a la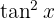 
utilizando una identidad pitagórica. Es decir,
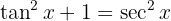
Por lo que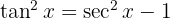 
. Así, la integral se convierte en
Como
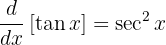
entonces la integral la podemos resolver de inmediato:
8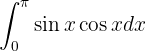 
Para esta integral no necesitamos utilizar ninguna identidad trigonométrica, ya que ni 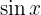ni 
se encuentran elevados a alguna potencia. Por lo tanto, podemos tomar
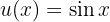
Por lo tanto,
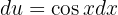
Observa que el cambio de variable no es biyectivo (uno-a-uno) en el dominio. Por lo tanto, será necesario regresar a la variable original antes de evaluar:
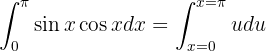
Calculamos la antiderivada:
Regresamos a la variable anterior:
Ahora evaluamos en los límites de la integral:
Que es el resultado que buscábamos.
Nota: si hubieramos tomado 
también habríamos podido calcular la intergral sencillamente.
9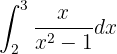 
Observa que en esta integral también tenemos un cambio de variable. En particular,
de donde se sigue que 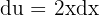. Por tanto,
Además,
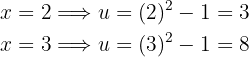
Por tanto, la integral se convierte en
Que al resolver y evaluar, obtenemos,
10 
Aunque no se vea inmediatamente, esta integral también se puede resolver con un cambio de variable (notemos que no todas las integrales se resuelven con cambio de variable). Tomemos,
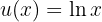
Por lo que
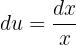
Luego, los límites se transforman en
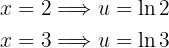
Por tanto, la integral se transforma en
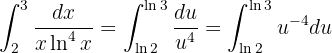
Así, resolviendo la integral y evaluando en los límites, tenemos,
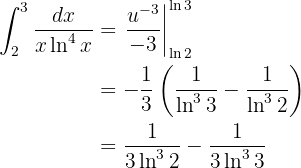
Que es lo más que podríamos simplificar.
11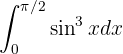 
En esta integral tenemos una potencia impar de 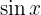. Necesitamos hacer un cambio de variable, donde 
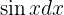será parte del diferencial de la nueva variable. Por tanto, separamos de la siguiente manera:
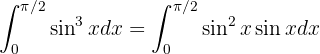
ahora utilizamos la identidad pitagórica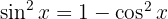 
para obtener
Podemos tomar el cambio de variable , por lo que 
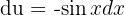, así
Además, el cambio de variable sí es inyectivo en el intervalo de integración, por lo tanto:
De este modo, la integral se convierte en
Al resolver la integral, obtenemos
12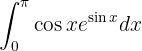 
Aquí podemos ver de inmediato que tenemos un cambio de variable. Tomamos
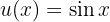
por lo que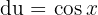 
. De este modo, la integral se vuelve
Que al integrar, se vuelve
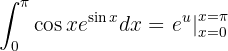
Regresamos a la variable anterior y evaluamos en los límites:
13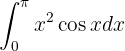 
Esta integral se resuelve por integración por partes. Primero resolvemos la integral sin preocuparnos por los límites y después evaluamos:
Como tenemos un polinomio multiplicando a , tomaremos 
y 
. De este modo
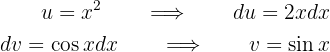
Por tanto, la integral es ahora
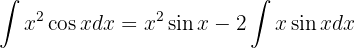
Volvemos a repetir el procedimiento, ahora con
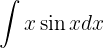
donde tomamos 
y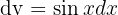 
. Aquí tenemos:
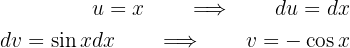
por lo tanto, esta seguna integral se vuelve
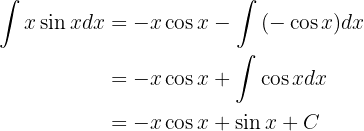
Sustituyendo en la integral original, tenemos
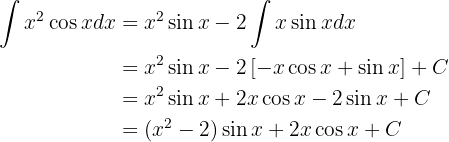
Ahora que tenemos la integral indefinida, evaluamos en los límites de integración:
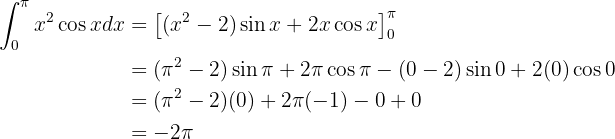
14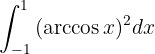 
Resolver integrales con funciones trigonométricas es un poco más complicado. Por lo regular, intentamos algún cambio de variable como
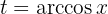
(aunque no siempre funciona). Despejando 
, tenemos 
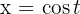. Por tanto,
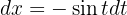
De aquí se sigue que
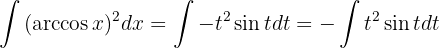
Esta integral también se resuelve por partes. Tomamos primero 
y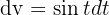 
, por tanto
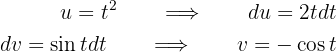
Y la integral se vuelve
Ahora tomamos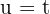 
y 
, así,
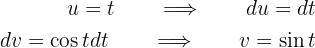
Con esto, la integral es
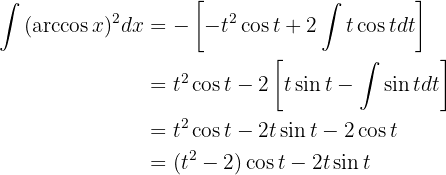
Podemos regresar a la variable interior o podemos cambiar los límites de la integral. Optamos por la segunda opción:
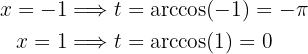
De este modo, la integral es
15 
Por último, esta integral la resolveremos con un cambio de variable para deshacernos del radical. Tomamos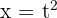 
, de este modo
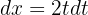
donde tomamos a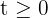 
. De este modo, 
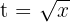y
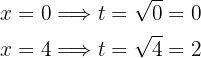
Por tanto, la integral se vuelve
Notemos que debemos transformar el integrando un poco. Observemos que
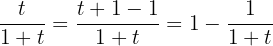
Así, tenemos
Que es el resultado de la integral.
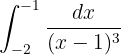
La primera integral la podemos resolver con la fórmula para integrar una potencia. Notemos primero que
Por lo que podemos utilizar la fórmula
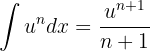
con el cambio de variable 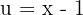y (notemos que en integrales definidas no es necesaria la constante de integración). De esta manera, obtenemos,
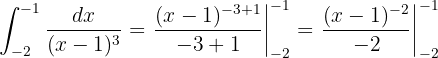
Es decir,
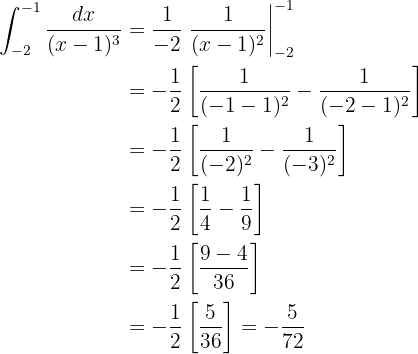
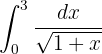
Al igual que en el caso anterior, esta integral la resolvemos con la fórmula de la integral de una potencia:
simplificamos un poco,
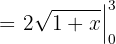
Y evaluamos en los límites de la integral:
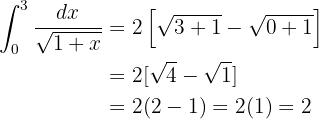
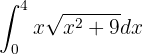
Esta integral se resuelve con un cambio de variable. Notemos que dentro de la raíz tenemos 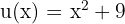. Si derivamos, tenemos 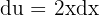; que al despejar , nos da
Además, como haremos cambio de variable, también debemos cambiar los límites de la integral. En particular,
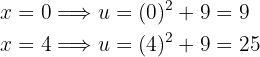
Por lo tanto, la integral se conviete en
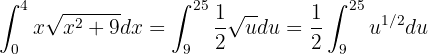
Ahora resolvemos la integral utilizando la fórmula de la integral de una potencia:
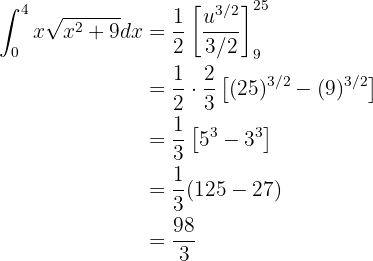
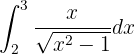
Al igual que en el caso anterior, hacemos el siguiente cambio de variable
donde, al derivar, tenemos 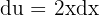. Por tanto, al despejar (ya que es lo que tenemos dentro del integrando), obtenemos
Ahora obtenemos los nuevos límites:
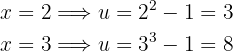
Por tanto, la integral se convierte en
Integramos con la fórmula de la integral de una potencia:
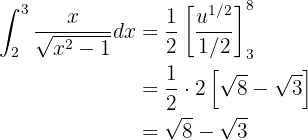
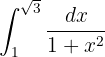
Esta integral se resuelve muy rápido si recordamos que
Por lo que la integral se resuelve de inmediato:
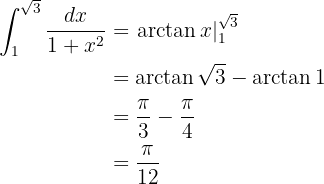
Recordemos que 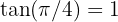y 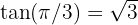(recordar esos valores es útil cuando deseamos encontrar los valores de la arco-tangente).
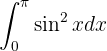
Para resolver esta integral necesitamos una identidad trigonométrica. En particular, como tenemos a 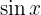elevado a una potencia par (2 en este caso), entonces necesitamos de alguna potencia que reduzca hasta alguna potencia impar. Esta la podemos obtener a partir de la identidad del ángulo doble para coseno:
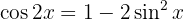
que, al despejar , obtenemos
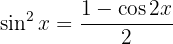
De esta forma, la integral se convierte en
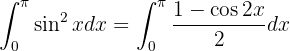
La cual ya se puede integrar de una forma más sencilla:
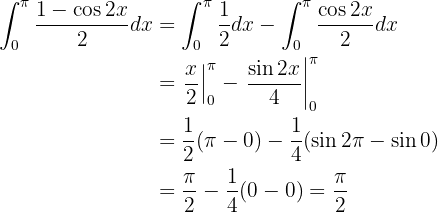
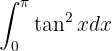
Es un poco complicado encontrar —por medio de prueba y error— alguna función tal que ). Por este motivo, es mejor transformar a la 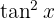utilizando una identidad pitagórica. Es decir,
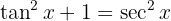
Por lo que 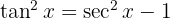. Así, la integral se convierte en
Como
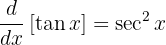
entonces la integral la podemos resolver de inmediato:
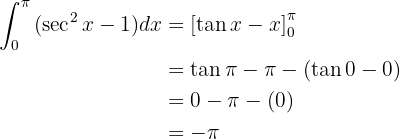
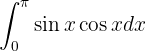
Para esta integral no necesitamos utilizar ninguna identidad trigonométrica, ya que ni 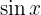ni se encuentran elevados a alguna potencia. Por lo tanto, podemos tomar
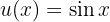
Por lo tanto,
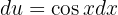
Observa que el cambio de variable no es biyectivo (uno-a-uno) en el dominio. Por lo tanto, será necesario regresar a la variable original antes de evaluar:
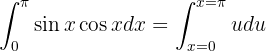
Calculamos la antiderivada:
Regresamos a la variable anterior:
Ahora evaluamos en los límites de la integral:
Que es el resultado que buscábamos.
Nota: si hubieramos tomado también habríamos podido calcular la intergral sencillamente.
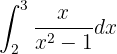
Observa que en esta integral también tenemos un cambio de variable. En particular,
de donde se sigue que 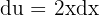. Por tanto,
Además,
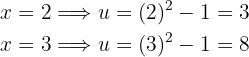
Por tanto, la integral se convierte en
Que al resolver y evaluar, obtenemos,
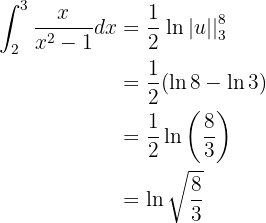
Aunque no se vea inmediatamente, esta integral también se puede resolver con un cambio de variable (notemos que no todas las integrales se resuelven con cambio de variable). Tomemos,
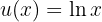
Por lo que
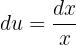
Luego, los límites se transforman en
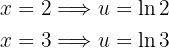
Por tanto, la integral se transforma en
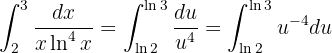
Así, resolviendo la integral y evaluando en los límites, tenemos,
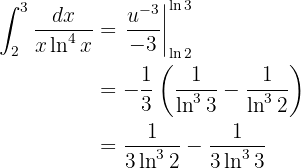
Que es lo más que podríamos simplificar.
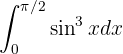
En esta integral tenemos una potencia impar de 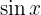. Necesitamos hacer un cambio de variable, donde 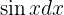será parte del diferencial de la nueva variable. Por tanto, separamos de la siguiente manera:
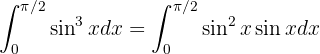
ahora utilizamos la identidad pitagórica 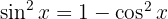para obtener
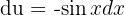Podemos tomar el cambio de variable , por lo que , así
Además, el cambio de variable sí es inyectivo en el intervalo de integración, por lo tanto:
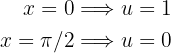
De este modo, la integral se convierte en
Al resolver la integral, obtenemos
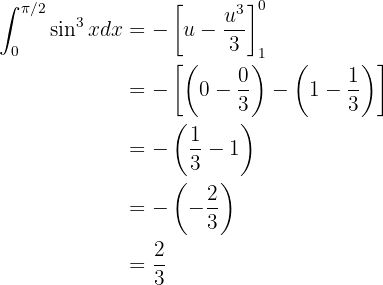
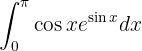
Aquí podemos ver de inmediato que tenemos un cambio de variable. Tomamos
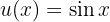
por lo que 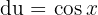. De este modo, la integral se vuelve
Que al integrar, se vuelve
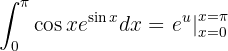
Regresamos a la variable anterior y evaluamos en los límites:
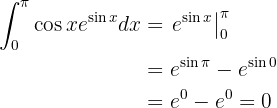
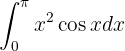
Esta integral se resuelve por integración por partes. Primero resolvemos la integral sin preocuparnos por los límites y después evaluamos:
Como tenemos un polinomio multiplicando a , tomaremos y . De este modo
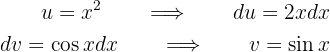
Por tanto, la integral es ahora
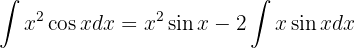
Volvemos a repetir el procedimiento, ahora con
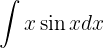
donde tomamos y 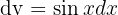. Aquí tenemos:
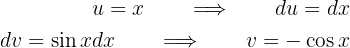
por lo tanto, esta seguna integral se vuelve
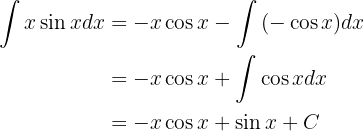
Sustituyendo en la integral original, tenemos
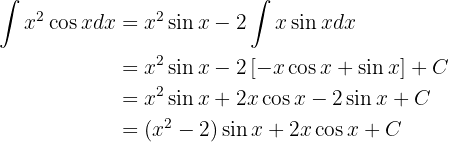
Ahora que tenemos la integral indefinida, evaluamos en los límites de integración:
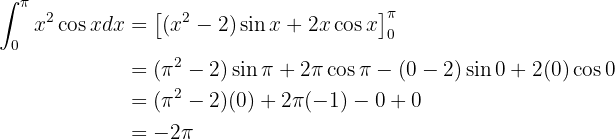
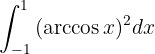
Resolver integrales con funciones trigonométricas es un poco más complicado. Por lo regular, intentamos algún cambio de variable como
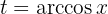
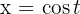(aunque no siempre funciona). Despejando , tenemos . Por tanto,
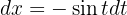
De aquí se sigue que
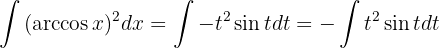
Esta integral también se resuelve por partes. Tomamos primero y 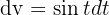, por tanto
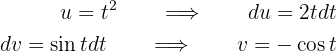
Y la integral se vuelve
Ahora tomamos 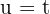y , así,
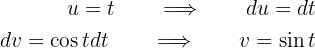
Con esto, la integral es
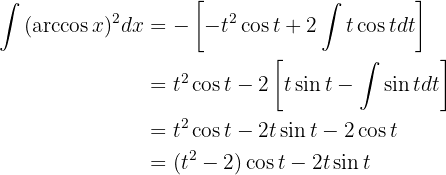
Podemos regresar a la variable interior o podemos cambiar los límites de la integral. Optamos por la segunda opción:
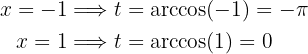
De este modo, la integral es
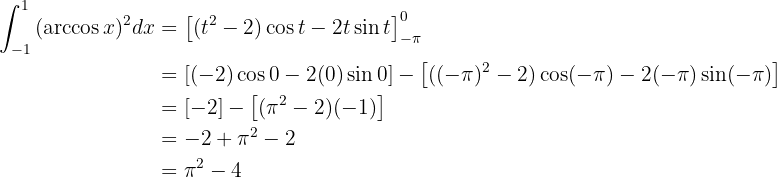
Por último, esta integral la resolveremos con un cambio de variable para deshacernos del radical. Tomamos 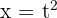, de este modo
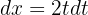
donde tomamos a 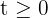. De este modo, 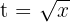y
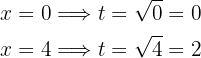
Por tanto, la integral se vuelve
Notemos que debemos transformar el integrando un poco. Observemos que
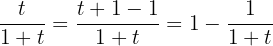
Así, tenemos
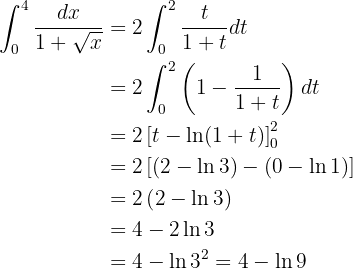
Que es el resultado de la integral.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hay un error en el integral de seno de x multiplicado por coseno de x.
Haciendo sustitución queda u^2/2 lo que indica que es sen(x)^2/2.
Hola en tu razonamiento estas bien, pero hay una cuestión para resolver este ejercicio hay dos formas una como tu dices y otra usando identidades trigonométricas, puedes comprobar que sale el mismo resultado en la integral definida.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.