Capítulos

Resolver las siguientesintegrales de tipo potencial:
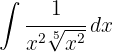
Para resolver la integral subimos el denominador y simplificamos las potencias, luego aplicamos la integral inmediata de potencias, es decir,  .
.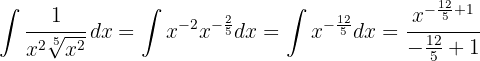
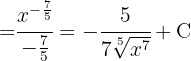
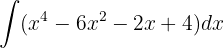
Comenzamos por separar la integral y aplicamos las integrales inmediatas correspondientes, es decir,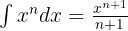 y
y  .
. 
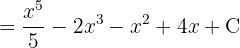

Separamos la integral en dos, convertimos la raíz a potencia, finalmente aplicamos la integral de potencias 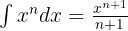
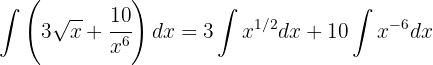
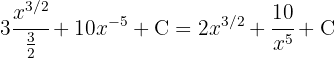
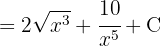

Comenzamos por separar la integral y simplificar las expresiones, para finalmente aplicar la integral de potencias 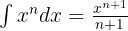

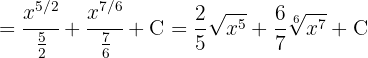

Comenzaremos por separar la integral y aplicar la integral inmediata de potencias 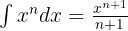
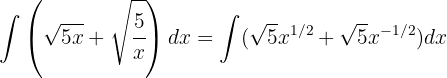


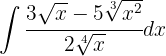
Separamos la integral y simplificamos las expresiones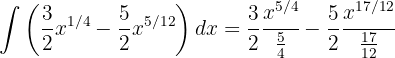
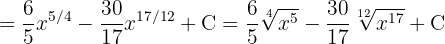
Para resolver la siguiente integral haremos un cambio de variable 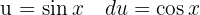

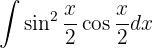
Para resolver la siguiente integral haremos un cambio de variable 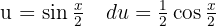

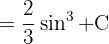
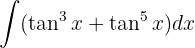
Comenzamos factorizando el término en común 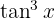 y utilizando la identidad
y utilizando la identidad 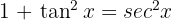
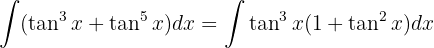
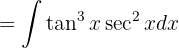 Haciendo el cambio de variable
Haciendo el cambio de variable 

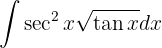
Para resolver la integral comenzamos haciendo el cambio de variable 
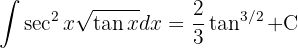
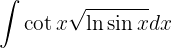
Para resolver la siguiente integral haremos el siguiente cambio de variable 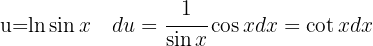 ,
,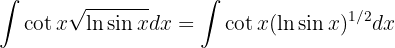
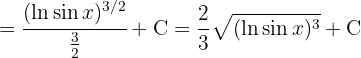
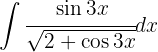
Para resolver la siguiente integral haremos el siguiente cambio de variable  ,
,
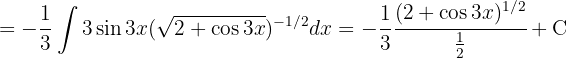
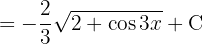

Para resolver la siguiente integral haremos el siguiente cambio de variable  ,
,
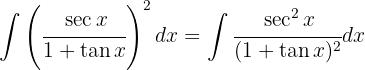

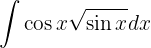
Para resolver la siguiente integral haremos el siguiente cambio de variable  ,
,
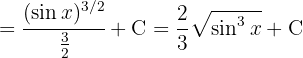
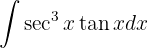
Para resolver la siguiente integral haremos el siguiente cambio de variable 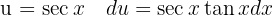 ,
,
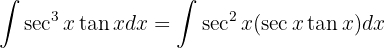

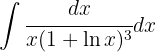
Para resolver la siguiente integral haremos el siguiente cambio de variable  ,
,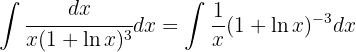
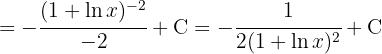

Comenzamos por escribir la raíz en su forma exponencial y luego simplificamos
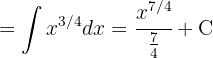


Comenzamos por escribir la raíz en su forma exponencial y luego simplificamos


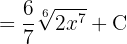
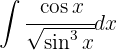
Comenzamos con un cambio de variable 
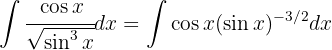


Observemos que al distribuir el cuadrado podemos simplificar la expresión y luego aplicamos un cambio de variable 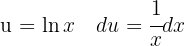

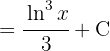

Aplicamos un cambio de variable 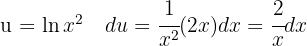
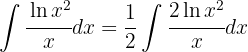


Comenzamos con un cambio de variable 
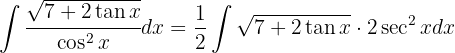
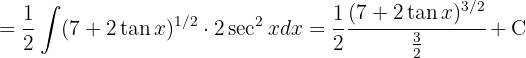
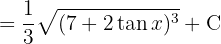
¿Conoces nuestras algebra clases?
Calcular lasintegrales logarítmicas:
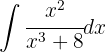
Comenzamos con un cambio de variable 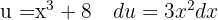 y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 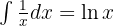

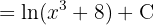
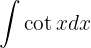
Comenzamos utilizando la definición 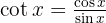 , luego con un cambio de variable
, luego con un cambio de variable 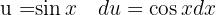 y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 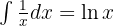
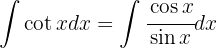
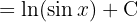

Comenzamos utilizando las identidades 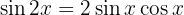 y
y 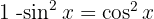 , simplificamos, hacemos un cambio de variable
, simplificamos, hacemos un cambio de variable 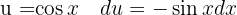 y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 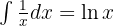
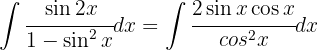

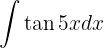
Comenzamos utilizando la definición 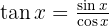 y hacemos un cambio de variable
y hacemos un cambio de variable  y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 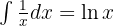
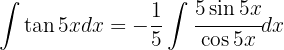
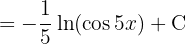
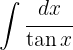
Comenzamos utilizando la definición 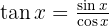 y hacemos un cambio de variable
y hacemos un cambio de variable 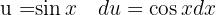 y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 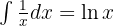
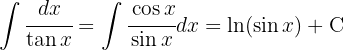

Comenzamos con un cambio de variable 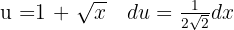 y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 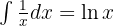

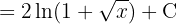
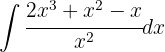
Comenzamos separando la integral y aplicando la integrales inmediatas correspondientes 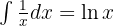
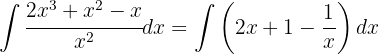
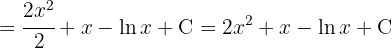
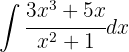
Comenzamos por separar y simplificar la integral, hacemos un cambio de variable  y aplicamos la integral inmediata
y aplicamos la integral inmediata 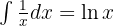
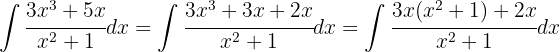

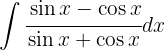
Comenzamos con un cambio de variable 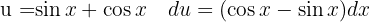 y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 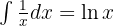
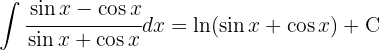

Comenzamos con un cambio de variable  y luego aplicamos la integral inmediata
y luego aplicamos la integral inmediata 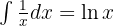


Comenzamos con la definición 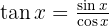 , luego un cambio de variable
, luego un cambio de variable 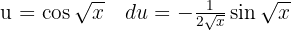 y aplicamos la integral inmediata
y aplicamos la integral inmediata 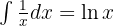


¿Buscas un profesor de mates? ¡Encuéntralo en Superprof!
Resolver las siguientesintegrales exponenciales:
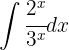
Para resolver la siguiente integral comenzamos por factorizar el exponente para poder aplicar la integral inmediata 

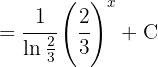
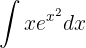
Comenzamos con un cambio de variable 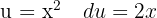 , y aplicamos la integral inmediata
, y aplicamos la integral inmediata 
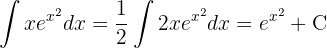
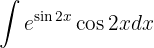
Comenzamos con el cambio de variable 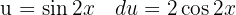 y aplicamos la integral inmediata
y aplicamos la integral inmediata 
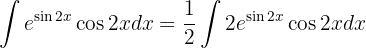
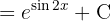
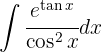
Para resolver la siguiente integral comenzamos con la definición 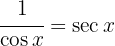 , aplicamos un cambio de variable
, aplicamos un cambio de variable 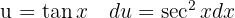 y finalmente utilizamos la integral inmediata
y finalmente utilizamos la integral inmediata 
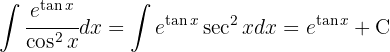

Para resolver la siguiente integral comenzamos haciendo un cambio de variable 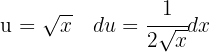 para poder aplicar la integral inmediata
para poder aplicar la integral inmediata 

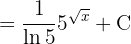
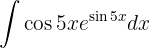
Para resolver la siguiente integral comenzamos con el cambio de variable 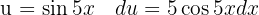 y finalmente utilizamos la integral inmediata
y finalmente utilizamos la integral inmediata 
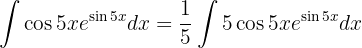
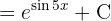

Para resolver la siguiente integral comenzamos con el cambio de variable 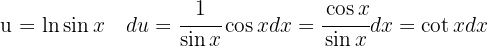 y finalmente utilizamos la integral inmediata
y finalmente utilizamos la integral inmediata 


Para resolver la siguiente integral comenzamos separando la integral, hacemos los cambios de variable correspondientes 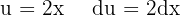 y
y  , finalmente utilizamos la integral inmediata
, finalmente utilizamos la integral inmediata 
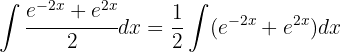
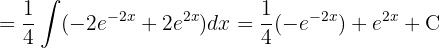
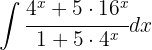
Para resolver la siguiente integral comenzamos simplificando la expresión y utilizamos la integral inmediata 
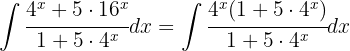
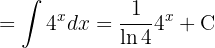
Calcular lasintegrales trigonométricas:

Para resolver la siguiente integral comenzamos por separar la integral y aplicar las integrales inmediatas  y
y 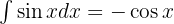
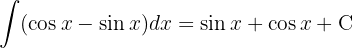

Para resolver la siguiente integral comenzamos por separar la integral y aplicar las integrales inmediatas 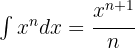 y
y 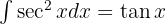
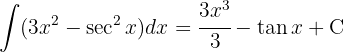
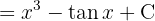
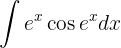
Para resolver la siguiente integral comenzamos con un cambio de variable 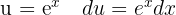 y aplicar la integral inmediata
y aplicar la integral inmediata 

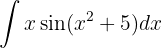
Para resolver la siguiente integral comenzamos con un cambio de variable  y aplicar la integral inmediata
y aplicar la integral inmediata 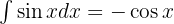
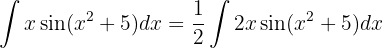
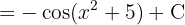

Para resolver la siguiente integral comenzamos con un cambio de variable 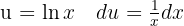 y aplicar la integral inmediata
y aplicar la integral inmediata 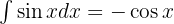
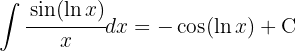
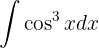
Para resolver la siguiente integral comenzamos utilizando la identidad 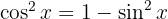 , separamos las integrales hacemos el cambio de variable
, separamos las integrales hacemos el cambio de variable  y aplicamos las integrales inmediatas
y aplicamos las integrales inmediatas  y
y 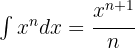

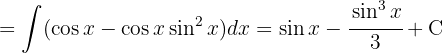

Para resolver la siguiente integral comenzamos utilizando las identidades  y
y 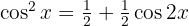
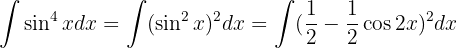
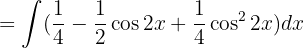
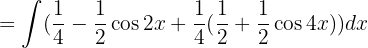
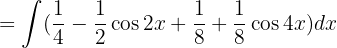

separamos las integrales hacemos cambios de variable 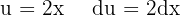 ,
,  y aplicamos la integral inmediata
y aplicamos la integral inmediata 
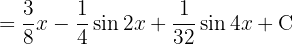
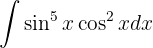
Reescribimos la integral usando identidades trigonométricas Aplicando la sustitución
Aplicando la sustitución  tenemos
tenemos

Expandiendo 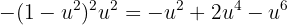
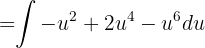

Sustituyendo de regreso la respuesta es


Reescribimos la integral usando identidades trigonométricas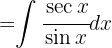
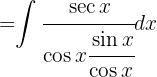

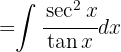
Aplicando una sustitución trigonométrica 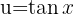 ,
, 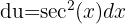 tenemos
tenemos
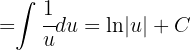
reemplazando de nuevo obtenemos el resultado
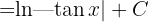
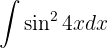
Reescribimos la integral usando identidades trigonométricas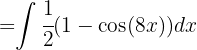

Estas ultimas integrales son iguales a
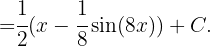
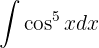
Reescribimos la integral usando identidades trigonométricas Aplicamos la sustitución
Aplicamos la sustitución 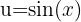 y obtenemos
y obtenemos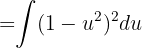
Ahora expandimos 

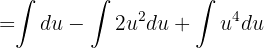
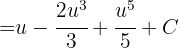
Sustituyendo de regreso se llega al siguiente resultado
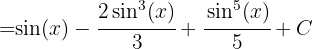

Aplicamos la sustitución  y
y  y obtenemos
y obtenemos
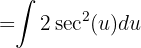
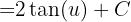
Sustituyendo de regreso se llega al siguiente resultado

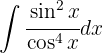
Reescribimos la integral usando identidades trigonométricas Aplicamos la sustitución
Aplicamos la sustitución 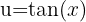 ,
, 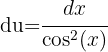 y obtenemos
y obtenemos
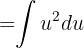
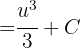
Sustituyendo de regreso se llega al siguiente resultado
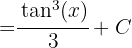
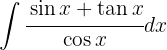
Aplicamos la sustitución 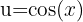 ,
, 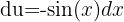 y obtenemos
y obtenemos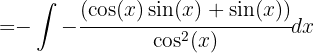
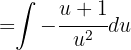
Expandiendo se sigue

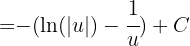
Sustituyendo de regreso se llega al siguiente resultado
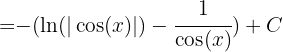
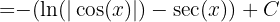
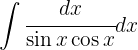
Reescribimos la integral usando identidades trigonométricas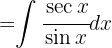
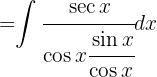

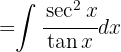
Aplicando una sustitución trigonométrica 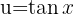 ,
, 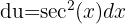 tenemos
tenemos
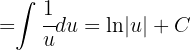
reemplazando de nuevo obtenemos el resultado
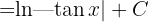
Resolver laintegrales trigonométricas:

Usamos la siguiente identidad trigonometrica Así que la integral queda de la siguiente forma
Así que la integral queda de la siguiente forma

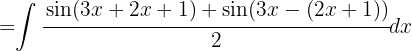
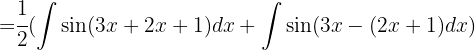
Dado que
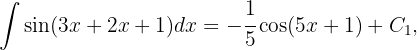
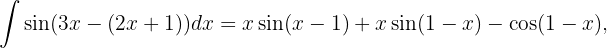
entonces el resultado final es
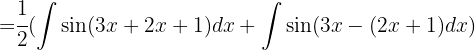
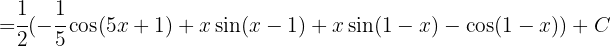

Reescribimos la integral usando identidades trigonométricas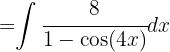

Ahora hacemos la sustitución  ,
,  y obtenemos
y obtenemos
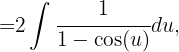
dado que

entonces la integral inicial es igual a
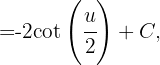
sustituyendo de regreso obtenemos que
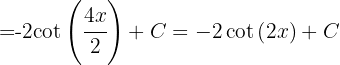
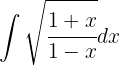
Primero hacemos la siguiente sustitución 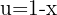 ,
, 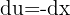 ,
,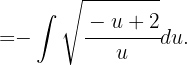 Ahora integrando por partes tenemos que
Ahora integrando por partes tenemos que
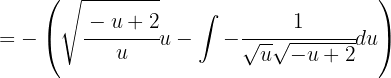
Dado que
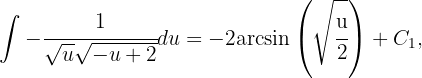
entonces
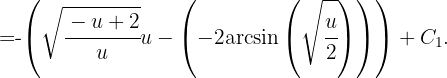
Sustituyendo de regreso tenemos que la integral es
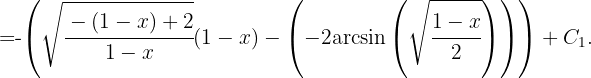


Reescribimos el integrando de la siguiente forma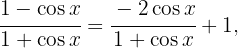 entonces
entonces


Dado que

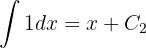
se sigue que la integral original es igual a
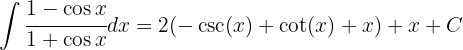
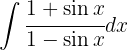
Reescribimos el integrando de la siguiente forma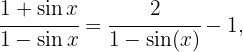 entonces
entonces
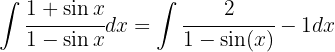
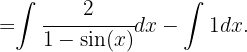
Dado que

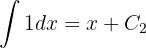
se sigue que la integral original es igual a

Si buscas un profesor de matematicas online, ¡encuéntralo en Superprof!
Calcular las integrales:

Usando la siguiente identidad trigonométrica podemos reescribir la integral
podemos reescribir la integral
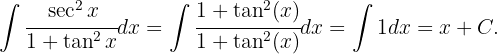
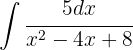
Reescribamos la integral de la siguiente forma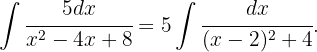 Ahora hacemos la sustitución
Ahora hacemos la sustitución 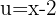 ,
, 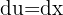 y obtenemos
y obtenemos
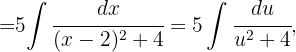
Aquí aplicamos la siguiente integral trigonométrica

Reemplazando de regreso llegamos a que el resultado es
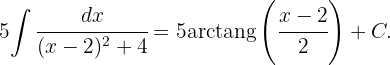

Expandimos el integrando de la siguiente forma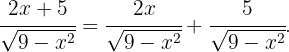 Así
Así
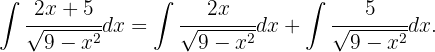
Dado que
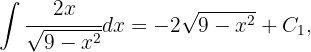
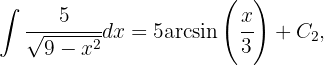
concluimos que la integral inicial es igual a
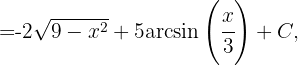

Reescribamos la integral de la siguiente forma Ahora hacemos la sustitución
Ahora hacemos la sustitución 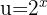 ,
, 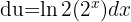 y obtenemos
y obtenemos

Aquí aplicamos la siguiente integral trigonométrica
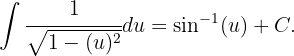
Reemplazando de regreso llegamos a que el resultado es
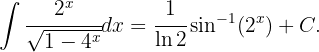
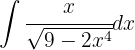
Primero aplicamos la siguiente sustitución 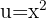 ,
, 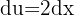 , entonces
, entonces Ahora aplicamos una sustitución trigonométrica con
Ahora aplicamos una sustitución trigonométrica con  y
y 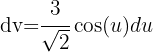 y obtenemos los siguiente
y obtenemos los siguiente
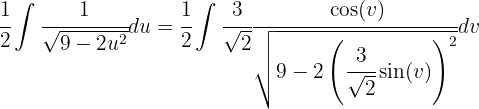
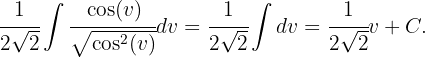
Sustituyendo de regreso se logra que



Primero aplicamos la sustitución 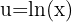 ,
,  y obtemos los siguiente
y obtemos los siguiente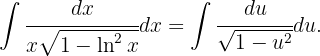 Dado que
Dado que

concluimos que
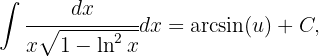
sustituyendo de regreso el resultado es
Problemas de integrales
Hallar una función  cuya derivada sea
cuya derivada sea 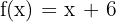 y tal que para
y tal que para  tome el valor
tome el valor 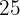 .
.
Sea Tomaremos el siguiente valor para la constante
Tomaremos el siguiente valor para la constante  . Ahora por el Teorema fundamental del Cálculo tenemos que
. Ahora por el Teorema fundamental del Cálculo tenemos que
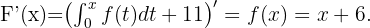
Integrando en  obtenemos que
obtenemos que
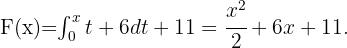
Finalmente evaluando en 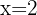 , se sigue que
, se sigue que
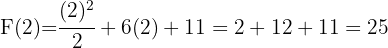
De las infinitas funciones primitivas de la función 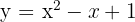 , ¿cuál es la que para
, ¿cuál es la que para 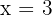 toma el valor
toma el valor  ?
?
Sea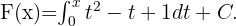 Tomaremos el siguiente valor para la constante
Tomaremos el siguiente valor para la constante  . Ahora por el Teorema fundamental del Cálculo tenemos que
. Ahora por el Teorema fundamental del Cálculo tenemos que
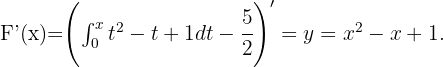
Integrando en  obtenemos que
obtenemos que
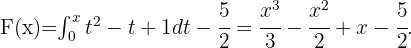
Finalmente evaluando en  , se sigue que
, se sigue que
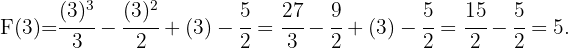
Hallar una recta cuya pendiente es  y pasa por él punto
y pasa por él punto 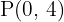 .
.
Sabemos que la ecuación punto-pendiente de una recta esta dada por donde
donde  es la pendiente de la recta y
es la pendiente de la recta y  es la intersección con el eje
es la intersección con el eje 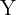 . También notemos que la derivada de la función que representa la recta es la pendiente de dicha recta. Así
. También notemos que la derivada de la función que representa la recta es la pendiente de dicha recta. Así
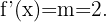
Ademas en nuestro caso sabemos que  y por lo tanto
y por lo tanto
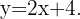
Escribe la función primitiva de 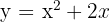 cuya representación gráfica pasa por él punto
cuya representación gráfica pasa por él punto 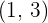 .
.
De nuevo este es un problema cuya solución usa el Teorema fundamental del cálculo. Sea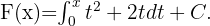 Tomaremos el siguiente valor para la constante
Tomaremos el siguiente valor para la constante  . Ahora por el Teorema fundamental del Cálculo tenemos que
. Ahora por el Teorema fundamental del Cálculo tenemos que

Integrando en  obtenemos que
obtenemos que

Finalmente evaluando en  , se sigue que grafica de
, se sigue que grafica de  pasa por
pasa por 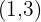 ,
,

Calcular la ecuación de la curva que pasa por 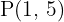 y cuya pendiente en cualquier punto es
y cuya pendiente en cualquier punto es 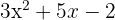 .
.
Recordemos que la derivada representa la pendiente de la función en un punto dado, entonces debemos encontrar una función primitiva a la función 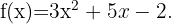 Sea
Sea Dado que
Dado que  debe pasar por
debe pasar por 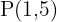 , tomaremos el siguiente valor para la constante
, tomaremos el siguiente valor para la constante 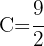 . Ahora por el Teorema fundamental del Cálculo tenemos que
. Ahora por el Teorema fundamental del Cálculo tenemos que
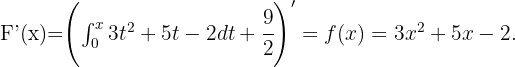
Integrando en  obtenemos que
obtenemos que
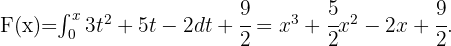
Finalmente evaluando en  , se sigue que ,
, se sigue que ,
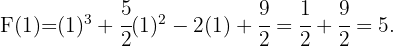
Así que nuestra respuesta es
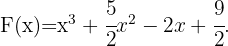
Hallar la primitiva de la función  , que se anula para
, que se anula para 
Sea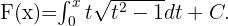 Tomaremos el siguiente valor para la constante
Tomaremos el siguiente valor para la constante  . Ahora por el Teorema fundamental del Cálculo tenemos que
. Ahora por el Teorema fundamental del Cálculo tenemos que

Integrando en  obtenemos que
obtenemos que

Finalmente evaluando en 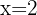 , se sigue que grafica de
, se sigue que grafica de  pasa por
pasa por 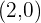 ,
,
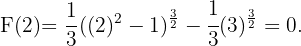
Asi que la función primitiva que buscamos esta dada por
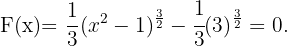













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Fe de erratas:
Ej. 3: sobra una raíz de x en el denominador antes del
Resultado final.
Ej.4: En el resultado final falta el signo menos.
Un saludo.
Hola revise los ejemplos de muchas ejercicios y no encontré los errores, podrías hacerme el favor de darme mas detalles para poder encontrarlos y quitar esos errores, seria de mucha ayuda.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hay un error en el integral de seno de x multiplicado por coseno de x.
Haciendo sustitución queda u^2/2 lo que indica que es sen(x)^2/2.
Hola en tu razonamiento estas bien, pero hay una cuestión para resolver este ejercicio hay dos formas una como tu dices y otra usando identidades trigonométricas, puedes comprobar que sale el mismo resultado en la integral definida.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.