Capítulos

¿Qué es una integral y para que sirve?
Principalmente la integral es conocida como la operación inversa de la derivada, la cual tiene la principal función de calcular el área bajo una curva, se encuentra ampliamente relacionada con el estudio del calculo infinitesimal.
Dato curioso:
¿ Habías notado que al resolver una integral, siempre agregamos un valor constante?
Por ejemplo:
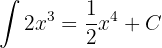
Si lo pensamos un poco, esto tiene mucho sentido, pues la derivada de cualquier constante es  , lo cual significa que al derivar una constante, esta desaparecerá, lo lógico es que al aplicar la operación contraria a la derivada, es decir, cuando integremos el valor
, lo cual significa que al derivar una constante, esta desaparecerá, lo lógico es que al aplicar la operación contraria a la derivada, es decir, cuando integremos el valor  , entonces tendremos como resultado una constante.
, entonces tendremos como resultado una constante.
Sobre los métodos para resolver integrales
Así como para las derivadas, las integrales cuentan con 2 métodos generales:
1 A través del concepto de limite
2 A través de fórmulas para casos específicos
Podría decirse que por cada forma de resolver una derivada, existe una forma de resolver una integral.
Ejemplo:
Dada la función 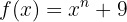
Su derivada es 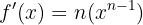 y la integral de esta ultima seria
y la integral de esta ultima seria 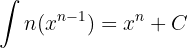
Ejercicios propuestos sobre integración
Integra las siguientes funciones:
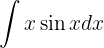
Integraremos esta función "por partes".
Recordemos que esto nos dice que

Decidamos que parte de la función será  y cual será
y cual será  . En nuestro caso los tomaremos de la siguiente manera
. En nuestro caso los tomaremos de la siguiente manera

y
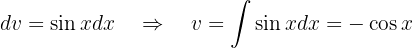
Sustituyendo estos valores en una fórmula de integración por partes tenemos que
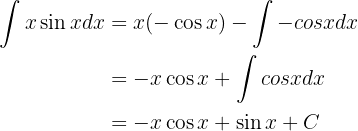
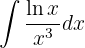
Integraremos esta función "por partes".
Recordemos que esto nos dice que

Decidamos que parte de la función será  y cual será
y cual será  . En nuestro caso los tomaremos de la siguiente manera
. En nuestro caso los tomaremos de la siguiente manera
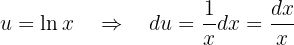
y
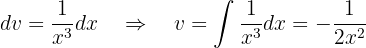
Sustituyendo estos valores en una fórmula de integración por partes tenemos que
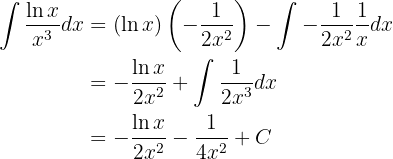
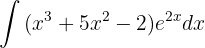
Integraremos esta función "por partes".
Recordemos que esto nos dice que

Decidamos que parte de la función será  y cual será
y cual será  . En nuestro caso los tomaremos de la siguiente manera
. En nuestro caso los tomaremos de la siguiente manera
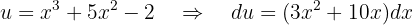
y

Sustituyendo estos valores en una fórmula de integración por partes tenemos que
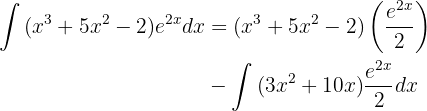
Volveremos a aplicar la integración por partes para integrar

en este caso  y
y  serán
serán

y
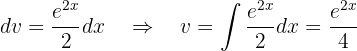
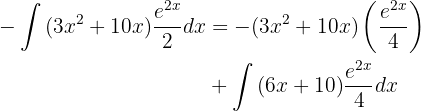
Por último volveremos a aplicar integración por partes para integrar

en este caso  y
y  serán
serán
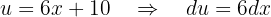
y
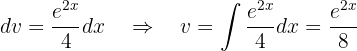
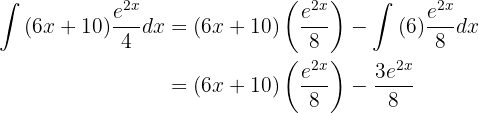
Sustituyendo todo esto en nuestra primer integral tenemos que
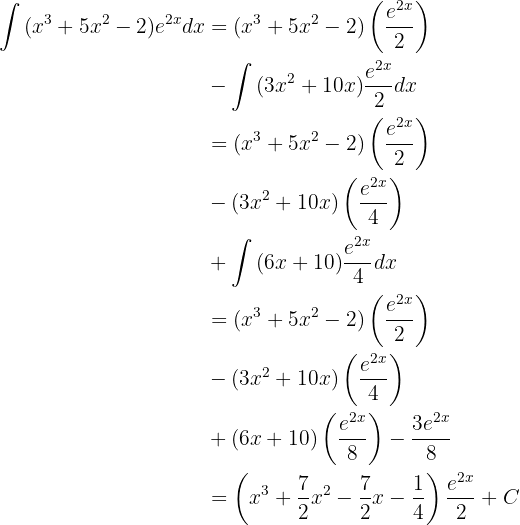
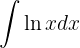
Integraremos esta función "por partes".
Recordemos que esto nos dice que

Decidamos que parte de la función será  y cual será
y cual será  . En nuestro caso los tomaremos de la siguiente manera
. En nuestro caso los tomaremos de la siguiente manera
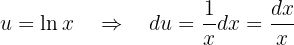
y
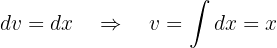
Sustituyendo estos valores en una fórmula de integración por partes tenemos que
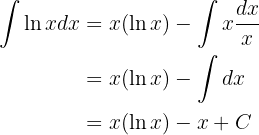
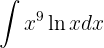
Integraremos esta función "por partes".
Recordemos que esto nos dice que

Decidamos que parte de la función será  y cual será
y cual será  . En nuestro caso los tomaremos de la siguiente manera
. En nuestro caso los tomaremos de la siguiente manera
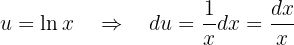
y
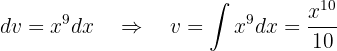
Sustituyendo estos valores en una fórmula de integración por partes tenemos que
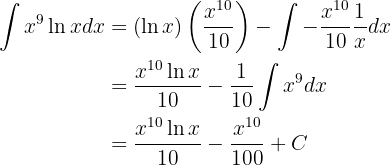
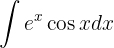
Integraremos esta función "por partes".
Recordemos que esto nos dice que

Decidamos que parte de la función será  y cual será
y cual será  . En nuestro caso los tomaremos de la siguiente manera
. En nuestro caso los tomaremos de la siguiente manera

y
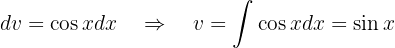
Sustituyendo estos valores en una fórmula de integración por partes tnnemos que
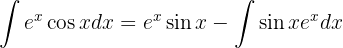
Volveremos a aplicar la integración por partes para integrar
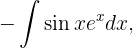
en este caso  y
y  serán
serán

y
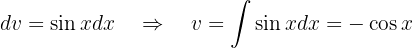
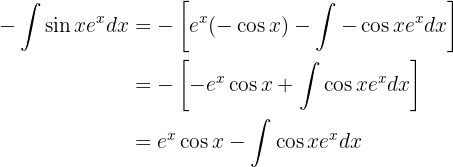
Sustituyendo todo esto en nuestra primer integral tenemos que aparece la integral que deseamos calcular del lado izquierdo y del lado derecho pero con signo negativo, por lo tanto lo único que necesitamos hacer es despejar la integral que deseamos encontrar
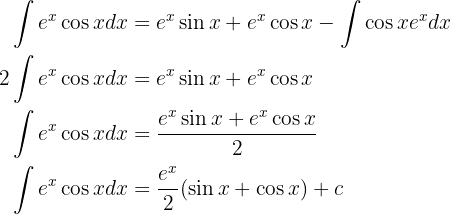
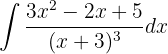
Para integrar esta función primero necesitamos simplificar dicha función

Para simplificarla y dejarla en una expresión fácil de integrarl aplicaremos fracciones parciales. No se explicará a fondo la teoría de fracciones parciales, sin embargo se intentará escribir cada paso para evitar confusión alguna.
Dado que el denominador es un polinomio de orden uno a la tercera potencia, tenemos que en general nuestra expresión se puede escribir como
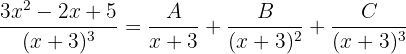
para ciertos números reales  ,
,  y
y  , para encontrar los valores de estas incógnitas debemos realizar las sumas y luego igualar los coeficientes de los términos del mismo grado, esto es
, para encontrar los valores de estas incógnitas debemos realizar las sumas y luego igualar los coeficientes de los términos del mismo grado, esto es
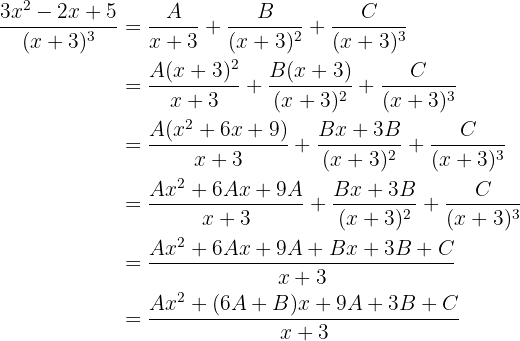
de esto se sigue que
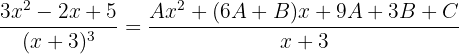
Por lo tanto, los numeradores son iguales
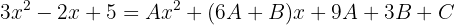
y los coeficientes de los términos de mismo grado tambien son iguales. Es decir

De la primera igualdad es directo que 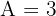 . Sustituyendo el valor de
. Sustituyendo el valor de  en la segunda igualdad tenemos
en la segunda igualdad tenemos
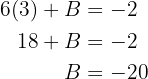
Sustituyendo el valor de 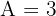 y
y  en la tercer igualdad tenemos que
en la tercer igualdad tenemos que
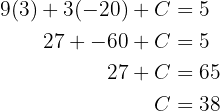
Así, tenemos que nuestra función es igual a

Ahora sí, procedamos a integrar. Usaremos método de cambio de variable, para ello tomaremos

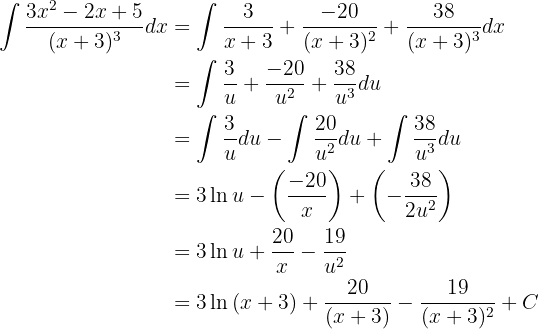

Integraremos usando el método de cambio de variable. Tomemos
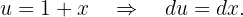
Notemos que, además,  . Así, sustituyendo en la integral original
. Así, sustituyendo en la integral original
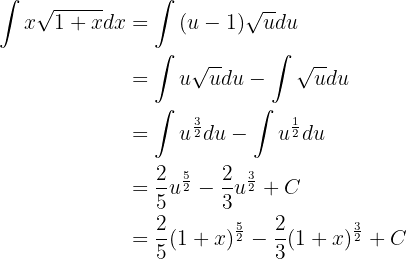
Integraremos usando el método de cambio de variable. Tomemos
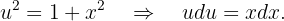
Notemos que, además,  . Así, sustituyendo en la integral original
. Así, sustituyendo en la integral original
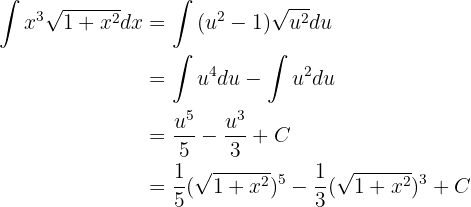
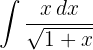
Integraremos usando el método de cambio de variable. Tomemos
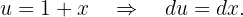
Notemos que, además,  . Así, sustituyendo en la integral original
. Así, sustituyendo en la integral original
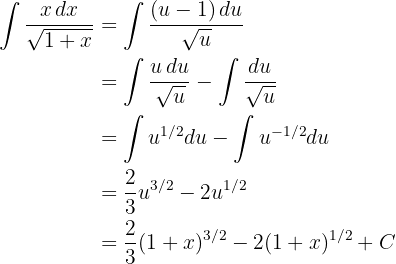
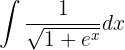
Integraremos usando el método de cambio de variable. Tomemos

Ahora despejemos los diferenciales
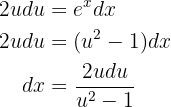
Así, sustituyendo en la integral original
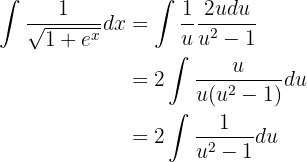
Aplicaremos fracciones parciales para simplificar dicha fracción y expresarla como suma de fracciones fácil de integrar. Tenemos que
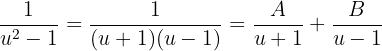
Desarrollando la última suma tenemos
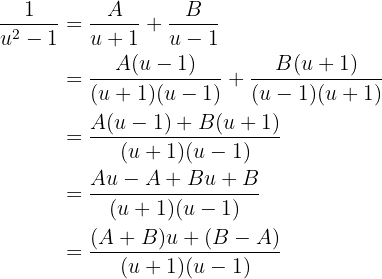
Igualando los numeradores tenemos que 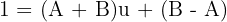 de donde se sigue directamente que
de donde se sigue directamente que

Notemos que de la primer igualdad se sigue directamente que  , y de la segunda se sigue que
, y de la segunda se sigue que 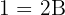 , por lo tanto
, por lo tanto

Notemos que entonces
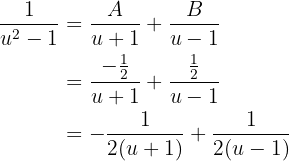
Sustituiremos ésto en la integral

de donde se sigue que, al sustituir el valor de  en términos de
en términos de  , esto es,
, esto es, 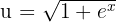
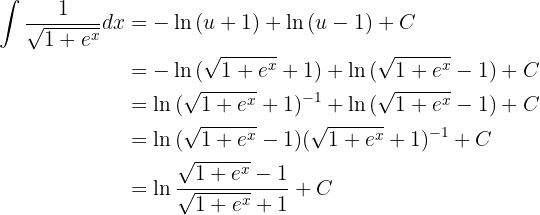
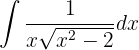
Integraremos por sustitución trigonométrica. Tomaremos
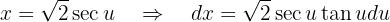
Sustituyendo estos valores en la integral
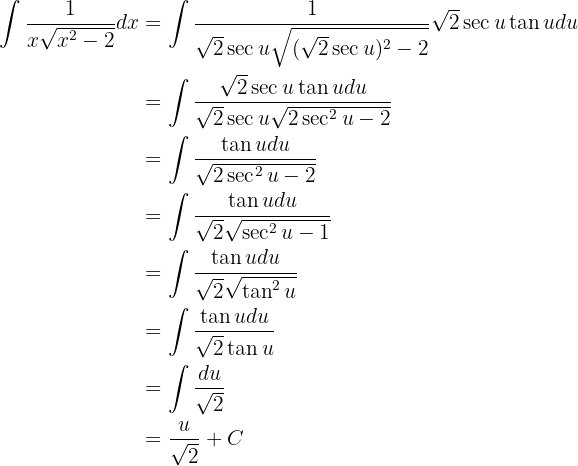
por último, para escribir de nuevo esto en términos de  , notemos que al hacer sustitución tomamos
, notemos que al hacer sustitución tomamos  , despejaremos
, despejaremos  de aquí
de aquí
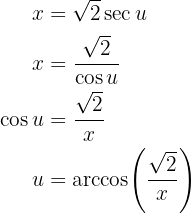
sustituyendo tenemos
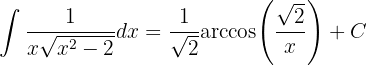
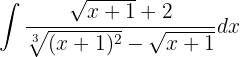
Integraremos utilizando el método de cambio de variable. Tomaremos
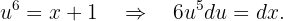
Sustituyendo estos valores en la integral obtenemos
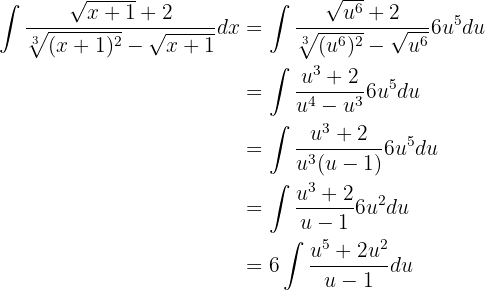
Ahora simplifiquemos la expresión dentro de la integral usando fracciones parciales. Tenemos que
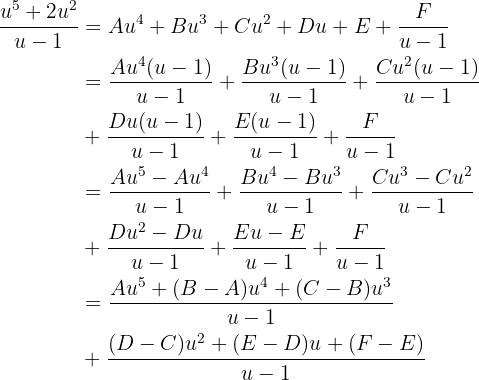
Esto nos da el siguiente sistema de ecuaciones
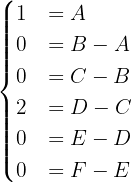
De donde se sigue que 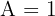 ,
,  ,
, 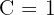 ,
,  ,
, 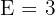 y
y 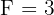 . Así, nuestra expresión es
. Así, nuestra expresión es
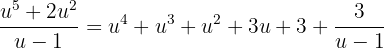
Sustituyendo en nuestra integral obtenemos
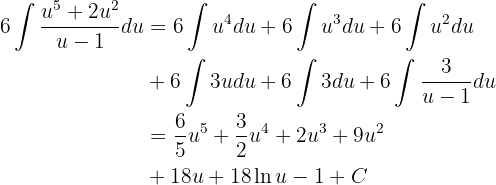
Solo nos falta escribirlo en términos de  , para esto notemos que
, para esto notemos que 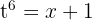 , por lo tanto,
, por lo tanto, 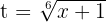 , sustituyendo obtenemos
, sustituyendo obtenemos
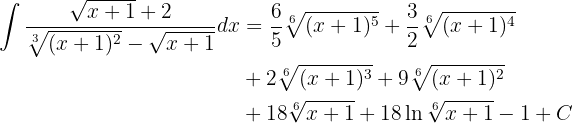
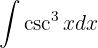
Integraremos usando el método de cambio de variable. Primero notemos que
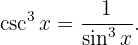
Nuestro cambio de variable será
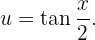
Derivando podemos ver que
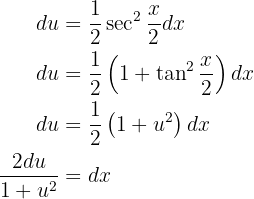
Dado que en la integral tenemos 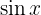 , debemos escribir esta función en término de
, debemos escribir esta función en término de 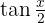 para poder sustituir la función en terminos de
para poder sustituir la función en terminos de  . Recordemos la siguiente identidad trigonométrica
. Recordemos la siguiente identidad trigonométrica
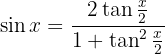
así, en pocas palabras tenemos que
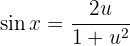
Sustituyendo en la integral obtenemos
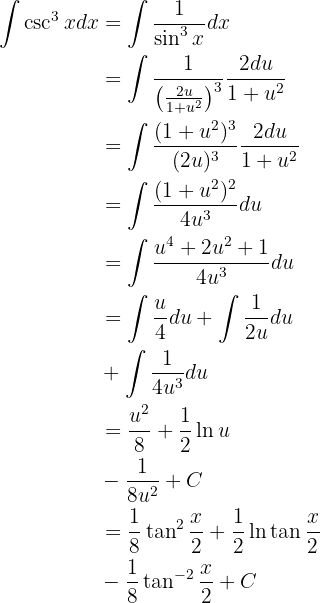
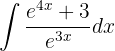
Integraremos utilizando el método de cambio de variable. Tomaremos
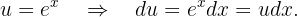
del diferencial se sigue que  . Ahora, sustituyendo esto en nuestra integral obtenemos
. Ahora, sustituyendo esto en nuestra integral obtenemos













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Fe de erratas:
Ej. 3: sobra una raíz de x en el denominador antes del
Resultado final.
Ej.4: En el resultado final falta el signo menos.
Un saludo.
Hola revise los ejemplos de muchas ejercicios y no encontré los errores, podrías hacerme el favor de darme mas detalles para poder encontrarlos y quitar esos errores, seria de mucha ayuda.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hay un error en el integral de seno de x multiplicado por coseno de x.
Haciendo sustitución queda u^2/2 lo que indica que es sen(x)^2/2.
Hola en tu razonamiento estas bien, pero hay una cuestión para resolver este ejercicio hay dos formas una como tu dices y otra usando identidades trigonométricas, puedes comprobar que sale el mismo resultado en la integral definida.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.