Las integrales trigonométricas que constan de productos de senos y cosenos son de la forma:
Para resolverlas aplicamos en los integrandos las siguientes fórmulas:
Fórmulas de producto de senos y cosenos
Se transforman los productos en sumas:
1
2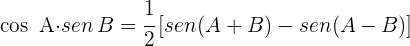
3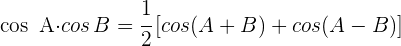
4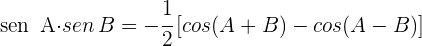
Integrales de producto de senos y cosenos
1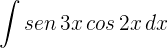
1Aplicamos la primera fórmula de producto de senos y cosenos con 
y 
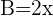
2Sustituimos en el integrando
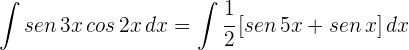
3Aplicamos las propiedades de las integrales
4Resolvemos las integrales
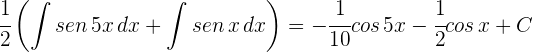
5La solución de la integral es
2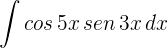
1Aplicamos la segunda fórmula de producto de senos y cosenos con 
y 
2Sustituimos en el integrando
3Aplicamos las propiedades de las integrales
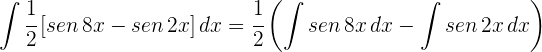
4Resolvemos las integrales
5La solución de la integral es
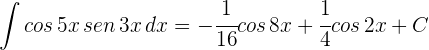
3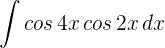
1Aplicamos la tercera fórmula de producto de senos y cosenos con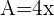 
y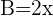
2Sustituimos en el integrando
3Aplicamos las propiedades de las integrales
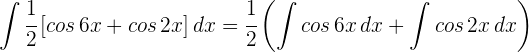
4Resolvemos las integrales
5La solución de la integral es
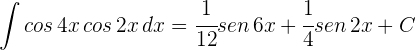
4
1Aplicamos la cuarta fórmula de producto de senos y cosenos con y 
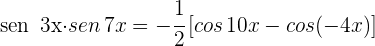
2Como coseno es una función par,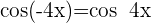 
y tenemos
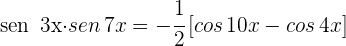
3Sustituimos en el integrando
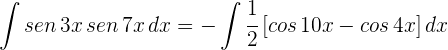
4Aplicamos las propiedades de las integrales
5Resolvemos las integrales
6La solución de la integral es
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
me puedes indicar por favor como desarrollar la integral e^x^2 sin (x) dx
Fe de erratas:
Ej. 3: sobra una raíz de x en el denominador antes del
Resultado final.
Ej.4: En el resultado final falta el signo menos.
Un saludo.
Hola revise los ejemplos de muchas ejercicios y no encontré los errores, podrías hacerme el favor de darme mas detalles para poder encontrarlos y quitar esos errores, seria de mucha ayuda.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))