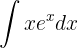
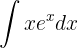
Resolvemos por integración por partes
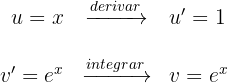
Sustituimos en la fórmula de integración por partes
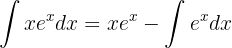
Resolvemos la nueva integral que aparece

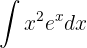
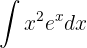
Resolvemos por integración por partes
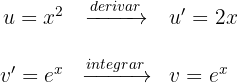
Sustituimos en la fórmula de integración por partes
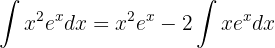
Resolvemos la segunda integral que aparece por integración por partes

Sustituimos en la fórmulade integración por partes

Resolviendo la nueva integral que aparece



Resolvemos por integración por partes
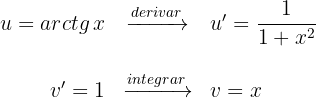
Sustituimos en la fórmula de integración por partes
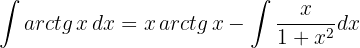
Resolvemos la nueva integral que aparece
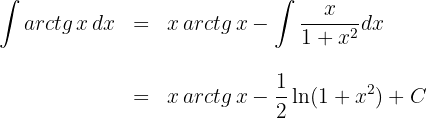
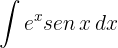
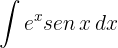
Resolvemos por integración por partes

Sustituimos en la fórmula de integración por partes
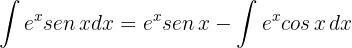
Resolvemos la segunda integral que aparece por integración por partes

Sustituimos en la fórmula de integración por partes
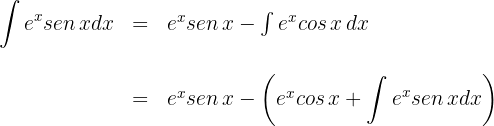
Resolviendo la nueva integral que aparece
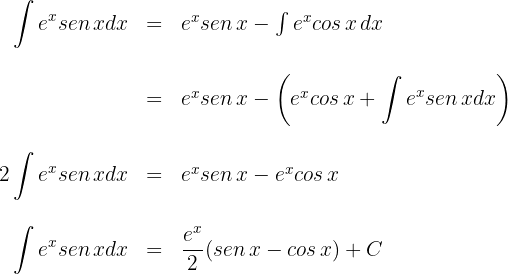
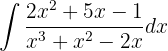
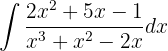
Resolvemos por fracciones parciales

Se efectúa la suma:
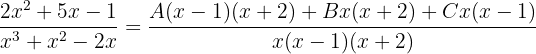
Como las dos fracciones tienen el mismo denominador, los numeradores han de ser iguales:

Calculamos los coeficientes de 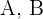 y
y 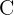 dando a la
dando a la  los valores que anulan al denominador.
los valores que anulan al denominador.
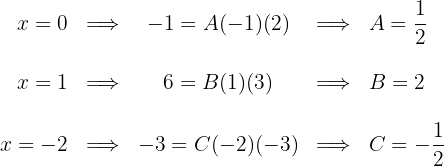
Se calculan las integrales de las fracciones simples:

Otra forma de hallar los coeficientes es realizando las operaciones e igualando coeficientes.

Igualamos coeficientes:
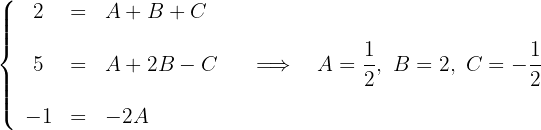
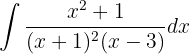
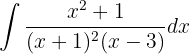
Resolvemos por fracciones parciales

Se efectúa la suma:
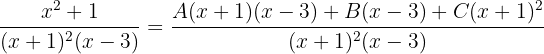
Como las dos fracciones tienen el mismo denominador, los numeradores han de ser iguales:
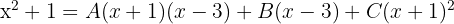
Para calcular los valores de 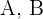 y
y 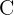 , damos a
, damos a  los valores que anulan al denominador y otro más
los valores que anulan al denominador y otro más
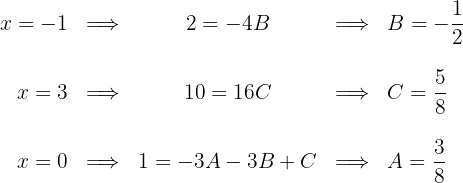
Se calculan las integrales de las fracciones simples:
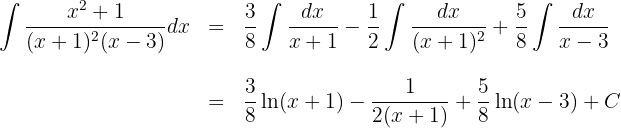
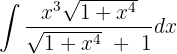
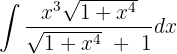
Empleamos la sustitución

Calculamos la diferencial en ambos lados

Sustituimos en la integral y resolvemos para 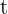

Sustituimos 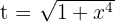 y obtenemos la solución en términos de
y obtenemos la solución en términos de 
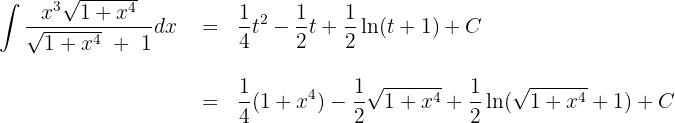
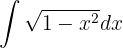
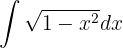
Empleamos la sustitución

Calculamos la diferencial en ambos lados
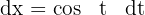
Sustituimos en la integral y resolvemos para 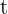

Sustituimos  en
en
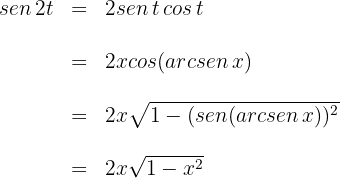
Sustituimos lo anterior y obtenemos la solución en términos de 
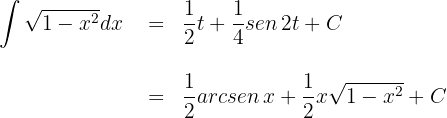
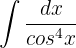
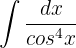
Empleamos la sustitución

Calculamos la diferencial en ambos lados
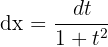
Sustituimos en la integral la expresión de la diferencial y la equivalencia 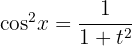
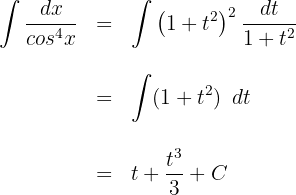
Sustituimos 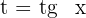 en la solución
en la solución



Empleamos la sustitución

Calculamos la diferencial en ambos lados
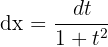
Sustituimos en la integral la expresión de la diferencial y las equivalencias 
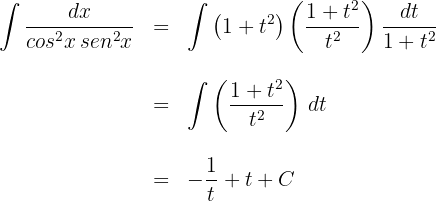
Sustituimos 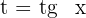 en la solución
en la solución
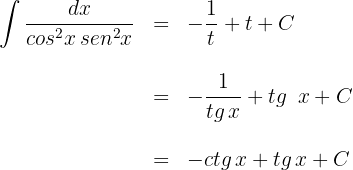
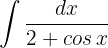
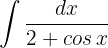
Empleamos la sustitución

Calculamos la diferencial en ambos lados

Sustituimos en la integral la expresión de la diferencial y la equivalencia 
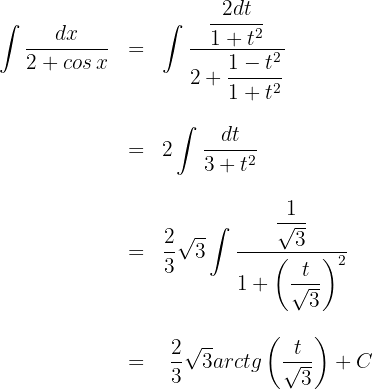
Sustituimos 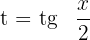 en la solución
en la solución



Empleamos la sustitución

Calculamos la diferencial en ambos lados
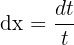
Sustituimos en la integral la expresión de la diferencial
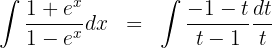
Resolvemos por fracciones parciales
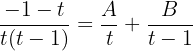
Se efectúa la suma:

Como las dos fracciones tienen el mismo denominador, los numeradores han de ser iguales:

Para calcular los valores de  y
y 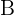 , damos a
, damos a 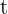 los valores que anulan al denominador
los valores que anulan al denominador

Se calculan las integrales de las fracciones simples:
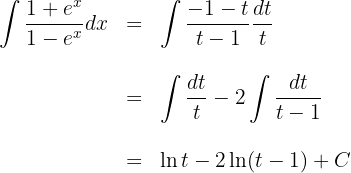
Sustituimos 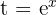 en la solución
en la solución




Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Fe de erratas:
Ej. 3: sobra una raíz de x en el denominador antes del
Resultado final.
Ej.4: En el resultado final falta el signo menos.
Un saludo.
Hola revise los ejemplos de muchas ejercicios y no encontré los errores, podrías hacerme el favor de darme mas detalles para poder encontrarlos y quitar esos errores, seria de mucha ayuda.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hay un error en el integral de seno de x multiplicado por coseno de x.
Haciendo sustitución queda u^2/2 lo que indica que es sen(x)^2/2.
Hola en tu razonamiento estas bien, pero hay una cuestión para resolver este ejercicio hay dos formas una como tu dices y otra usando identidades trigonométricas, puedes comprobar que sale el mismo resultado en la integral definida.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.