Bienvenidos a nuestra sección dedicada al cálculo de volúmenes de funciones mediante el uso del cálculo integral. Este es un tema de gran importancia en las matemáticas y la física, y su dominio es esencial para abordar una variedad de problemas relacionados con áreas y volúmenes en el espacio tridimensional. En esta guía, los acompañaremos paso a paso en el viaje de calcular volúmenes utilizando técnicas integrales.
El proceso de calcular el volumen de una función implica la división de un sólido tridimensional en elementos infinitesimales, y la suma de estos elementos utilizando integrales definidas para encontrar el volumen total. Esto nos permite comprender y cuantificar la extensión de objetos en el espacio tridimensional con precisión.
¡Comencemos a calcular integrales!
Hallar el volumen del tronco de cono engendrado por la rotación alrededor 
del área limitada por 
.
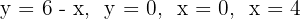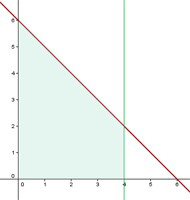
1Representamos gráficamente el problema
2Sustituimos en la fórmula para encontrar el volumen
3Para resolver la integral, consideramos la sustitución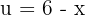 
y calculamos su derivada
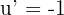
4Empleamos la fórmula de integración
5Al tratarse de una integral definida, podemos prescindir de la constante de integración
6Evaluamos en los extremos de integración
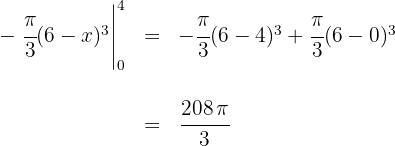
Luego el volumen es 
Hallar el volumen engendrado por las superficies limitadas por la curva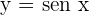 
y las rectas 
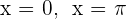, al girar en torno al eje OX
1Representamos gráficamente el problema
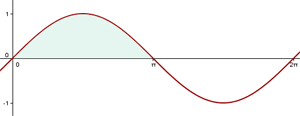
2Sustituimos en la fórmula para encontrar el volumen
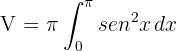
3Para resolver la integral, consideramos la identidad trigonométrica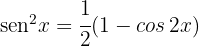 
, por lo que la integral se expresa
4Al tratarse de una integral definida, podemos prescindir de la constante de integración
5Evaluamos en los extremos de integración
Luego el volumen es 
Calcular el volumen engendrado por una semionda de la sinusoide 
, al girar alrededor del eje .
1Representamos gráficamente el problema
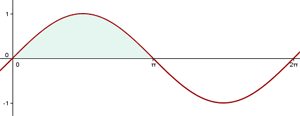
Observamos que la sinusoide corresponde a la figura del ejercicio 2
2Sustituimos en la fórmula para encontrar el volumen
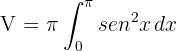
3Para resolver la integral, consideramos la identidad trigonométrica 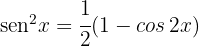, por lo que la integral se expresa
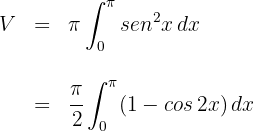
4Al tratarse de una integral definida, podemos prescindir de la constante de integración
5Evaluamos en los extremos de integración
Luego el volumen es
Hallar el volumen del cuerpo revolución engendrado al girar alrededor del eje , la región determinada por la función 
, el eje de abscisas y las rectas .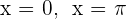
1Sustituimos en la fórmula para encontrar el volumen
2Desarrollamos el integrando
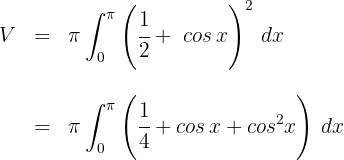
3Consideramos la identidad trigonométrica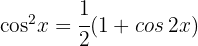 
. Al tratarse de una integral definida, podemos prescindir de la constante de integración
4Evaluamos en los extremos de integración
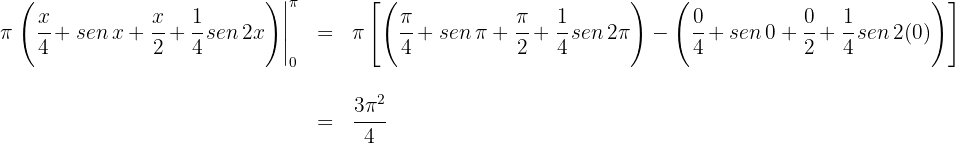
Luego el volumen es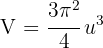 
Hallar el volumen engendrado por el círculo 
al girar alrededor del eje .
1Expresamos la ecuación del círculo en su forma ordinaria
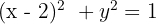
2El centro de la circunferencia es 
y el radio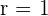 
. Los puntos de corte con el eje son:
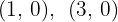
3A partir de la cuación general del círculo obtenemos la función
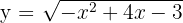
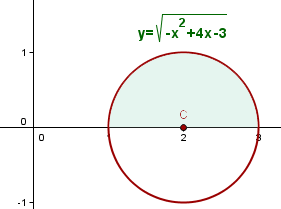
4Sustituimos en la fórmula para encontrar el volumen
5Desarrollamos el integrando
6Al tratarse de una integral definida, podemos prescindir de la constante de integración
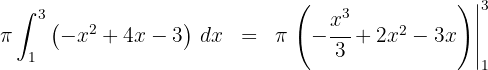
7Evaluamos en los extremos de integración
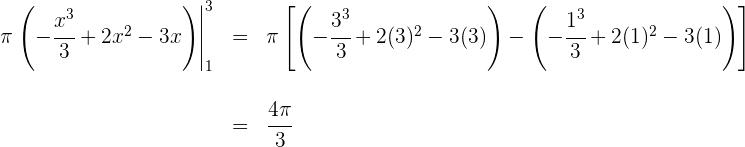
Luego el volumen es 
Calcular el volumen engendrado al girar alrededor del eje el recinto limitado por las gráficas de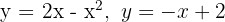 
.
1Para encontrar los puntos de intersección de la recta y la parábola, resolvemos el sistema
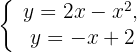
Igualamos y factorizamos para obtener
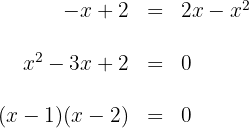
Las raíces son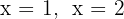 
. Luego los puntos de intersección son: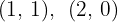 
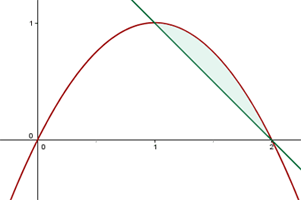
2Sustituimos en la fórmula para encontrar el volumen
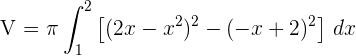
3Desarrollamos el integrando
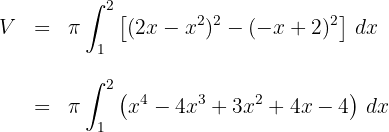
4Al tratarse de una integral definida, podemos prescindir de la constante de integración
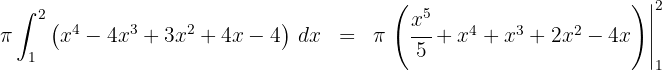
5Evaluamos en los extremos de integración
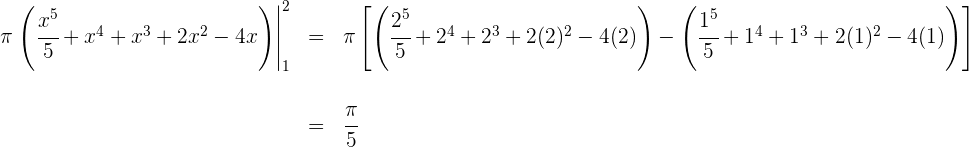
Luego el volumen es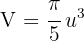 
Calcular el volumen del cuerpo engendrado al girar alrededor del eje el recinto limitado por las gráficas de 
1Para encontrar los puntos de intersección de la recta y la parábola, resolvemos el sistema
Igualamos y factorizamos para obtener
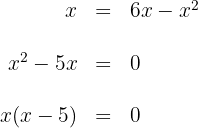
Las raíces son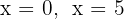 
. Luego los puntos de intersección son: 
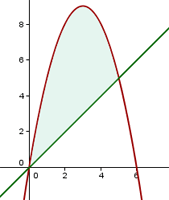
2Sustituimos en la fórmula para encontrar el volumen
3Desarrollamos el integrando
4Al tratarse de una integral definida, podemos prescindir de la constante de integración
5Evaluamos en los extremos de integración
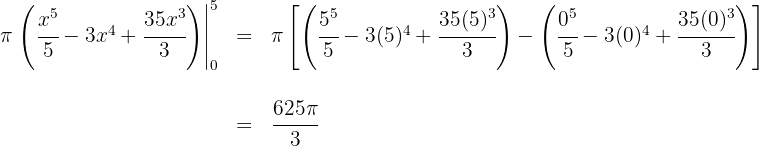
Luego el volumen es 
Calcular el volumen que engendra un triángulo de vértices 
al girar 
alrededor del eje .
1Representamos graficamente
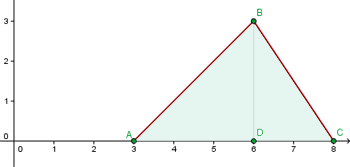
Las ecuaciones de las rectas que pasan por 
y 
son
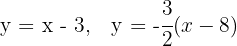
2Sustituimos en la fórmula para encontrar el volumen, observando que para el segmento de recta consideramos el intervalo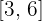 
y para el segmento de recta consideramos el intervalo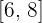 
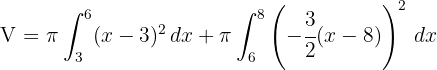
3Desarrollamos el integrando
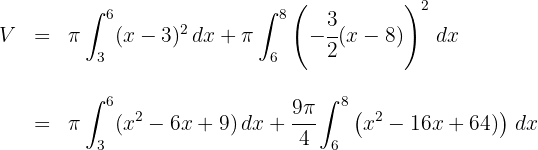
4Al tratarse de una integral definida, podemos prescindir de la constante de integración
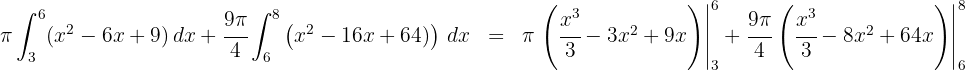
5Evaluamos en los extremos de integración y obtenemos
Luego el volumen es 
Hallar el volumen de la figura engendrada al girar la elipse 
alrededor del eje .
1Representamos graficamente
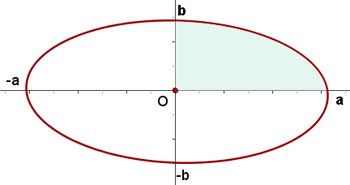
2El centro de la elipse es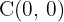 
. Los puntos de corte con el eje son:
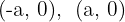
3A partir de la cuación de la elipse, obtenemos la función
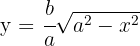
Por ser la elipse una curva simétrica, el volumen pedido es 2 en veces el volumen engendrado por el arco entre 
y 
.
4Sustituimos en la fórmula para encontrar el volumen
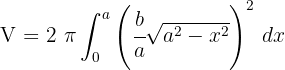
5Desarrollamos el integrando
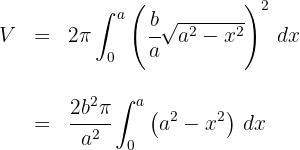
6Al tratarse de una integral definida, podemos prescindir de la constante de integración
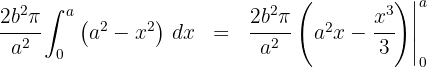
7Evaluamos en los extremos de integración
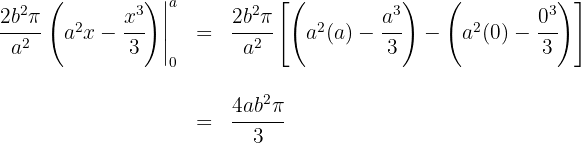
Luego el volumen es 
Calcular el volumen del cilindro engendrado por el rectángulo limitado por las rectas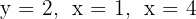 
, y el eje al girar alrededor de este eje.
1Sustituimos en la fórmula para encontrar el volumen
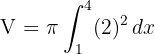
2Al tratarse de una integral definida, podemos prescindir de la constante de integración
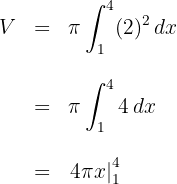
3Evaluamos en los extremos de integración
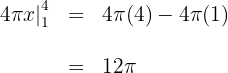
Luego el volumen es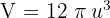 
Calcular el volumen de la esfera de radio 
.
1Partimos de la ecuación de la circunferencia 
2Girando un semicírculo en torno al eje de abscisas se obtiene una esfera
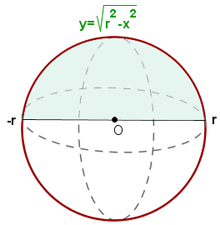
3A partir de la cuación de la circunferencia, obtenemos la función
4Sustituimos en la fórmula para encontrar el volumen
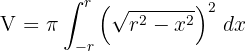
5Desarrollamos el integrando
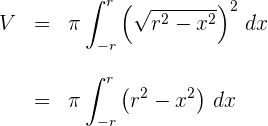
6Al tratarse de una integral definida, podemos prescindir de la constante de integración
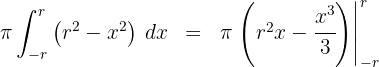
7Evaluamos en los extremos de integración
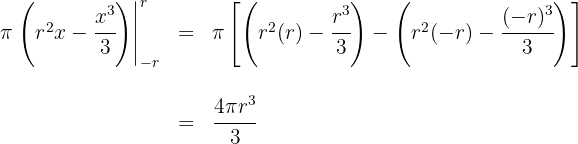
Luego el volumen es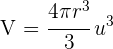 
Calcular el volumen engendrado por la rotación del área limitada por la parábola 
y la recta 
, alrededor del eje 
.
1Representamos graficamente
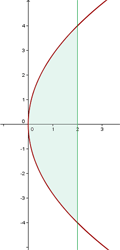
Como gira alrededor del eje , aplicamos:
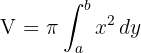
El volumen será la diferencia del engendrado por la recta y el engendrado por la parábola entre los extremos 
.
Como la parábola es simétrica con respecto al eje , el volumen es igual a dos veces el volumen engendrado entre 
.
2Sustituimos en la fórmula para encontrar el volumen
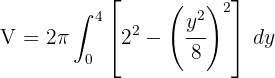
3Al tratarse de una integral definida, podemos prescindir de la constante de integración
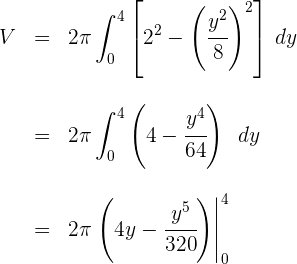
4Evaluamos en los extremos de integración
Luego el volumen es 
Hallar el volumen del elipsoide engendrado por la elipse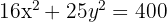 
, al girar alrededor del eje .
1Expresamos la elipse en su ecuación ordinara
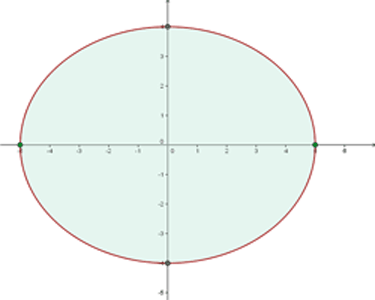
2El centro de la elipse es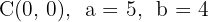 
. Aplicamos la fórmula obtenida en el ejercicio 9
3Sustituyendo los valores conocidos, obtenemos
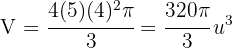
Encuentra el volumen del s´lido de revolución generado al revolucionar la función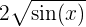 
, definida en el intervalo 
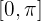, alrededor del eje OX.
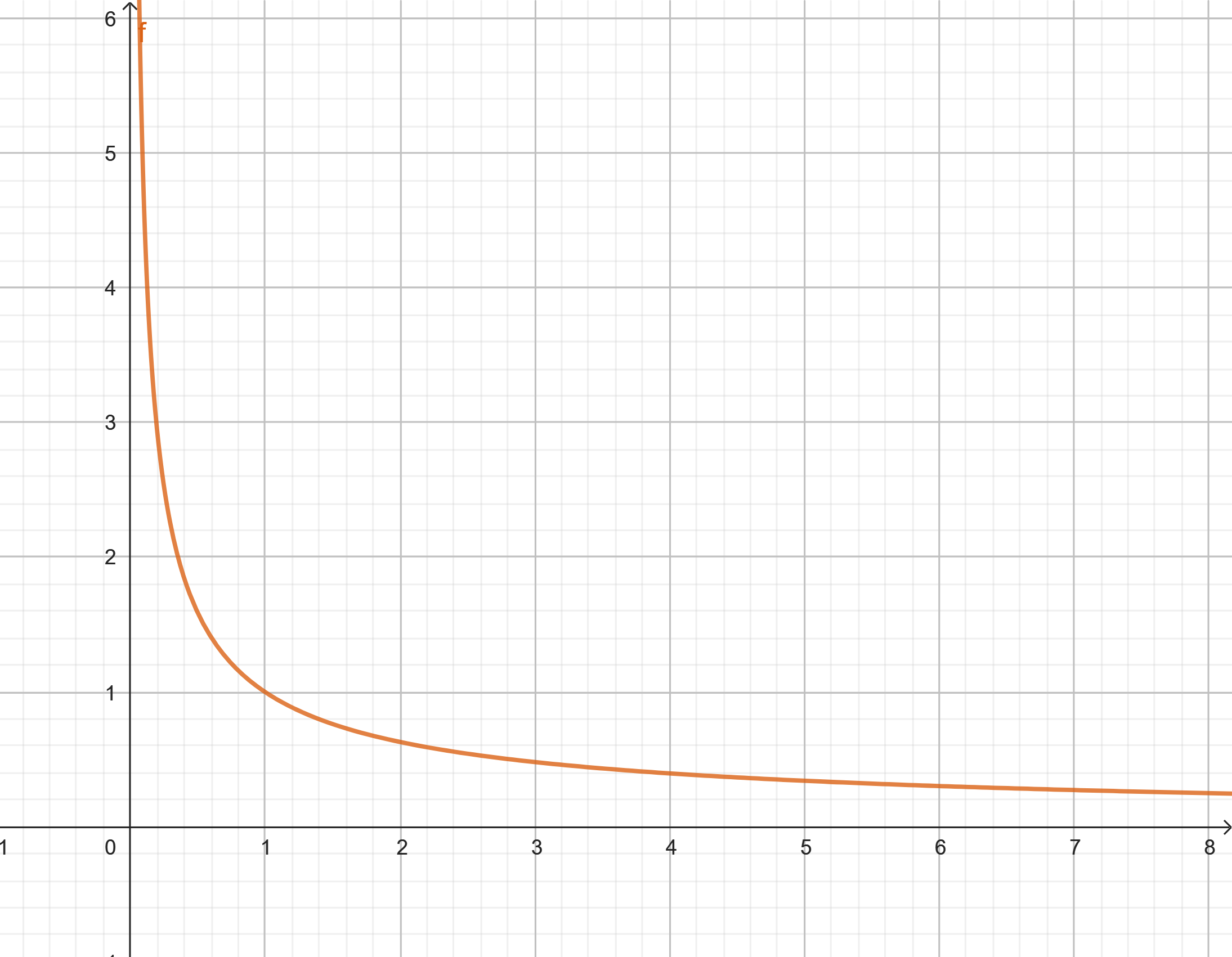
1Ilustramos la función.
2Calculamos la integral:
Sea 
para 
.
a Dibuja la gráfica de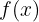 
.
b Calcula el área de la región acotada por 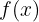y el eje OX en el intervalo 
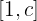, donde 
.
c Calcula el volumen del sólido de revolución generado al revolucionar la región del inciso (b) alrededor del eje OX.
d ¿Qué le ocurre al área que calculaste en el inciso (b) si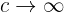 
? ¿Y al volumen del sólido de revolución?
a
b Calculamos la integral en el intervalo 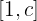. Es decir, el área bajo la curva:
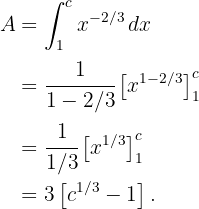
c Ahora, revolucionamos esta misma área alrededor del eje OX:
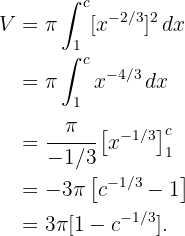
d Si 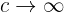en el resultado del inciso (b), tenemos
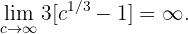
Es decir, el área bajo la curva va a infinito si el intervalo que tomamos va a infinito. Sin embargo, notemos que
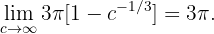
Es decir, el volumen del sólido se mantiene acotado.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hay un error en el integral de seno de x multiplicado por coseno de x.
Haciendo sustitución queda u^2/2 lo que indica que es sen(x)^2/2.
Hola en tu razonamiento estas bien, pero hay una cuestión para resolver este ejercicio hay dos formas una como tu dices y otra usando identidades trigonométricas, puedes comprobar que sale el mismo resultado en la integral definida.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.